Порядок выполнения работы

1. Сформируйте набор статистический данных ошибки использую датчик случайных чисел(не менее 50 значений)

2. Определите и удалите грубые ошибки.

3. Оцените нормальность закона распределения ошибок.

4. Проверьте полученные расчеты использую автоматизированную системы.

5. Занесите полученные данные в таблицу(набор данных ошибки, грубые ошибки, значения критерия χ2.)

Приложение

Таблица 1

Интеграл вероятностей ,

t	Сотые доли t
	0	1	2	3	4	5	6	7	8	9
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4	0,0000 0398 0793 1179 1554 1915 2257 2580 2881 3159 3413 3643 3849 4032 4192 4332 4452 4554 4641 4713 4772 4821 4861 4893 4918	0040 0438 0832 1217 1591 1950 2291 2611 2910 3186 3437 3665 3869 4049 4207 4345 4463 4564 4649 4719 4778 4826 4864 4896 4920	0080 0478 0871 1255 1628 1985 2324 2642 2939 3212 3461 3686 3888 4066 4222 4357 4474 4573 4656 4726 4783 4830 4868 4898 4922	0120 0517 0910 1293 1664 2019 2357 2673 2967 3238 3458 3708 3907 4082 4236 4370 4484 4582 4664 4732 4788 4834 4871 4901 4925	0160 0557 0948 1331 1700 2054 2389 2703 2995 3264 3508 3729 3925 4099 4251 4382 4495 4591 4671 4738 4793 4838 4875 4904 4927	0199 0596 0987 1368 1736 2088 2422 2734 3023 3289 3531 3749 3944 4115 4265 4394 4505 4599 4678 4744 4798 4842 4878 4906 4929	0239 0636 1026 1406 1772 2123 2454 2764 3051 3315 3554 3770 3962 4131 4279 4406 4515 4608 4686 4750 4803 4846 4881 4909 4931	0279 0675 1064 1443 1808 2157 2486 2794 3078 3340 3577 3790 3980 4147 4292 4418 4525 4616 4693 4756 4808 4850 4884 4911 4932	0319 0714 1103 1480 1844 2190 2517 2823 3106 3365 3599 3810 3997 4162 4306 4429 4535 4625 4699 4761 4812 4854 4887 4913 4934	0359 0753 1141 1517 1879 2224 2549 2852 3133 3389 3621 3830 4015 4177 4319 4441 4545 4633 4706 4767 4817 4857 4890 4916 4936

Таблица допускает линейную интерполяцию с ошибкой до .

Пример. Вычислить Ф (1,614).

Решение. Берем из таблицы два значения Ф (1,61) = 0,4463 и Ф (1,62) = 0,4474 с разностью 0,0011 и вводим поправку на относи­тельное приращение аргумента (1,614—1,61)/0,01 =0,4:

Ф(1,614) = Ф (1,61) + 0,0011*0,4 = 0,4467.

Таблица 2

Величины, связанные с интегралом вероятностей Ф (t); функция

t = t(Р) является обратной для Р=2Ф(t)

t	Ф(t)	1-2Ф(t)	1-P	t=t(Р)	P
2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4,0 4,1 4,2 4,3 4,4 4,5 4,6 4,7 4,8 4,9 5,0	0,49379 0,49534 0,49653 0,49744 0,49813 0,49865 0,49903 0,49931 0,49952 0,49966 0,499767 0,499841 0,499892 0,499927 0,499952 0,499968 0,499979 0,499987 0,499991 0,499995 0,4999966 0,4999979 0,4999987 0,4999992 0,4999995 0,4999997	0,01242 0,00932 0,00693 0,00511 0,00373 0,00270 0,00194 0,00137 0,00097 0,00067 0,000465 0,000318 0,000216 0,000145 0,000096 0,000063 0,000041 0,000027 0,000017 0,000011 0,0000068 0,0000041 0,0000025 0,0000016 0,0000009 0,0000006	0,05 0,04 0,03 0,02 0,01 0,009 0,008 0,007 0,006 0,005 0,004 0,003 0,002 0,001 0,0009 0,0008 0,0007 0,0006 0,0005 0,0004 0,0003 0,0002 0,0001 10 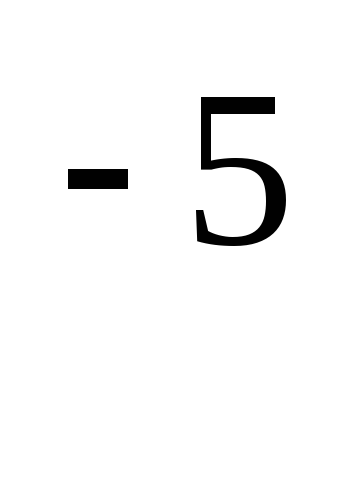10 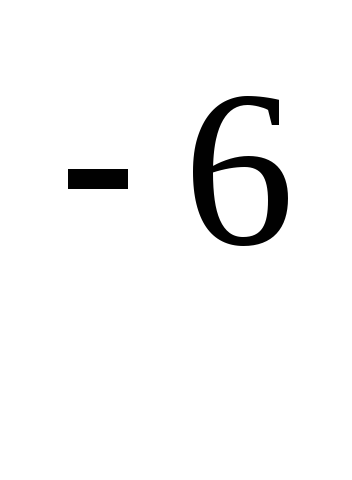10	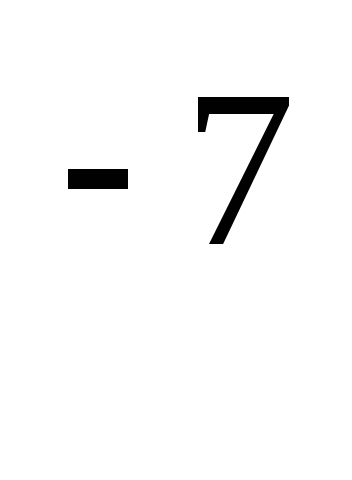1,960 2,054 2,170 2,326 2,576 2,612 2,652 2,697 2,748 2,807 2,878 2,968 3,090 3,291 3,320 3,353 3,390 3,432 3,481 3,540 3,615 3,720 3,891 4,417 4,892 5,327	0,95 0,96 0,97 0,98 0,99 0,991 0,992 0,993 0,994 0,995 0,996 0,997 0,998 0,999 0,9991 0,9992 0,9993 0,9994 0,9995 0,9996 0,9997 0,9998 0,9999 1-10 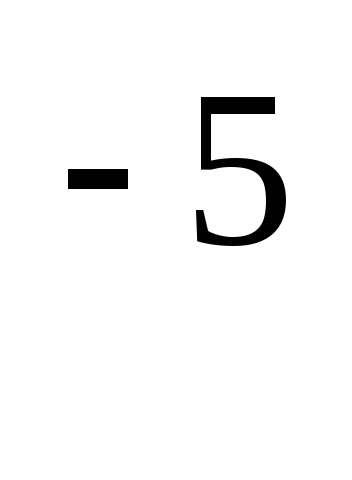1-10 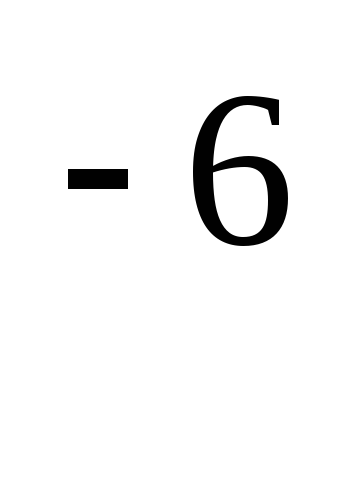1-10

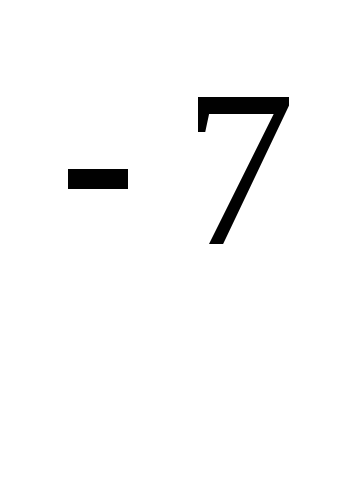
В таблице значений Ф(t) ошибка линейной интерполяции убывает с увеличением значений t; она не превосходит:

10- в интервале (2,5; 3,2); 10- в интервале (3,2; 3,9);

10- в интервале (3,9; 4,5); 10- в интервале (4,5; 5,0).

Таблица 3

Критические значения для браковки «выскакивающих» значенийx*

Р	0,95	0,98	0,99	0,999	Р	0,95	0,98	0,99	0,999
n					n
5 6 7 8 9 10 11 12 13 14 15 16 17 18	3,04 2,78 2,62 2,51 2,43 2,37 2,33 2,29 2,26 2,24 2,22 2,20 2,18 2,17	4,11 3,64 3,36 3,18 3,05 2,96 2,89 2,83 2,78 2,74 2,71 2,68 2,66 2,64	5,04 4,36 3,69 3,71 3,54 3,41 3,31 3,23 3,17 3,12 3,08 3,04 3,01 2,98	9,43 7,41 6,37 5,73 5,31 5,01 4,79 4,62 4,48 4,37 4,28 4,20 4,13 4,07	20 25 30 35 40 45 50 60 70 80 90 100	2,145 2,105 2,079 2,061 2,048 2,038 2,030 2,018 2,009 2,003 1,998 1,994 1,960	2,602 2,541 2,503 2,476 2,456 2,441 2,429 2,411 2,399 2,389 2,382 2,377 2,326	2,932 2,852 2,802 2,768 2,742 2,722 2,707 2,683 2,667 2,655 2,646 2,639 2,576	3,979 3,819 3,719 3,652 3,602 3,565 3,532 3,492 3,462 3,439 3,423 3,409 3,291

Линейная интерполяция по аргументу n может дать ошибку до 10при 20<n<60 и ошибку до 10при 60 <п < 100.

При n > 100 критические значения с точностью до 10можно вычислить по формуле

Таблица 3

Распределение Стьюдента. Значения

Р	0,90	0,95	0,98	0,99	0,999
k
4 5 6 7 8 9 10 11 12 13 14 15 16 18 20 25 30 35 40 45 50 60 70 80 90 100	2,132 2,015 1,943 1,895 1,860 1,833 1,812 1,796 1,782 1,771 1,761 1,753 1,746 1,734 1,725 1,708 1,697 1,689 1,684 1,679 1,676 1,671 1,667 1,664 1,662 1,660 1,645	2,776 2,571 2,447 2,365 2,306 2,262 2,228 2,201 2,179 2,160 2,145 2,131 2,120 2,103 2,086 2,060 2,042 2,030 2,021 2,014 2,008 2,000 1,995 1,990 1,987 1,984 1,960	3,747 3,365 3,143 2,998 2,896 2,821 2,764 2,718 2,681 2,650 2,624 2,602 2,583 2,552 2,528 2,485 2,457 2,437 2,423 2,412 2,403 2,390 2,381 2,374 2,368 2,364 2,326	4,604 4,032 3,707 3,499 3,355 3,250 3,169 3,106 3,055 3,012 2,977 2,947 2,921 2,878 2,845 2,787 2,750 2,724 2,704 2,689 2,677 2,660 2,648 2,639 2,632 2,626 2,576	8,610 6,859 5,959 5,405 5,041 4,781 4,587 4,487 4,318 4,221 4,140 4,073 4,015 3,922 3,850 3,725 3,646 3,591 3,551 3,522 3,497 3,460 3,436 3,416 3,401 3,391 3,291

Интерполяция значений допустима только по аргу­менту k. При 16 < k < 60 ошибка линейной интерполяции не пре­восходит 7*10для Р = 0,999,4*10 для Р = 0.99 и 2*10для Р < 0,98. При 60 < k < 100 ошибка линейной интерполяции не пре­восходит 10.

При k > 100 с точностью до 10имеет место формула

Таблица 4

Критические значения при надёжности Р и числе степеней свободыk.

Р	0,80	0,90	0,95	0,98	0,99	0,995	0,998	0,999
k
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 22 24 26 28 30	5,99 7,29 8,56 9,80 11,03 12,24 13,44 14,63 15,80 17,00 18,20 19,30 20,5 21,60 22,80 23,90 25,00 27,30 29,60 31,80 34,00 36,30	7,78 9,24 10,64 12,02 13,36 14,68 15,99 17,30 18,50 19,80 21,10 22,30 23,50 24,80 26,00 27,20 28,40 30,80 33,20 35,60 37,90 40,30	9,49 11,07 12,59 14,07 15,51 16,09 18,30 19,70 21,00 22,40 23,70 25,00 26,30 27,60 28,90 30,10 31,40 33,90 36,40 38,90 41,30 43,80	11,67 13,39 15,03 16,60 18,20 19,70 21,20 22,60 24,10 25,50 26,90 28,30 29,60 31,00 32,30 33,70 35,00 37,70 40,30 42,90 45,40 48,00	13,28 15,09 16,80 18,50 20,10 21,70 23,20 24,70 26,20 27,70 29,10 30,60 32,00 33,40 34,80 36,20 37,60 40,30 43,00 45,60 48,30 50,90	14,9 16,3 18,6 20,3 21,9 23,6 25,2 26,8 28,3 29,8 31,3 32,7 34,2 35,7 37,2 38,6 40,0 42,7 45,5 48,2 51,0 53,7	16,9 18,9 20,7 22,6 24,3 26,1 27,7 29,4 31,0 32,5 34,0 35,6 37,1 38,6 40,1 41,6 43,1 45,9 48,7 51,5 54,3 57,1	18,5 20,5 22,5 24,3 26,1 27,9 29,6 31,3 32,9 34,5 36,1 37,7 39,3 40,8 42,3 43,8 45,3 48,3 51,2 54,1 56,9 59,7

При k > 30 для критического значения можно пользоваться приближенным значением

,

где t(P) , берется из таблицы 2.