3. Альтернативы Фредгольма. Теорема Шаудера о неподвижной точке.

Следующие теоремы составляют содержание теории Рисса – Шаудера (в упрощенном варианте), являющейся обобщением фредгольмовской теории интегральных уравнений.

Теорема 5 (первая теорема Фредгольма). Пусть А – ли­нейный вполне непрерывный оператор в банаховом простран­стве X. Следующие четыре утверждения эквивалентны:

а) уравнение (3) имеет решение при любой правой части у;

b) уравнение (4) имеет только тривиальное решение;

c) уравнение (3*) имеет решение при любой правой частит;

d) уравнение (4*) имеет только тривиальное решение.

Если выполнено одно из условий а), b), c), d), то операторы I – A и I – А* непрерывно обратимы.

Доказательство проведем по схеме а)  b)  c)  d)  а).

I. a)  b). Дано R(I – А) = Х, т. е. множество значений оператора I – А совпадает с X. Допустим, что b) не выполнено, т. е. подпространство нулей оператора I – A нетривиально:

N₁ = {x  X: x – Ax = 0}  {0}.

Пусть x₁N₁ и x₁  0. Рассмотрим уравнение (I– А)х =x₁. По условию а) оно имеет решения. Пусть х₂ – одно из них. Имеем (I – А)²х₂ = (I – A)x₁ = 0, т. e х₂  N₂ = {x  X: (I - А)²х = 0}, причем N₁  N₂ и включение строгое, так как x₂ N₂, но х₂  N₁, иначе оказалось бы, что x₁ = 0. Продолжая эти рассуждения, получим цепочку подпространств

N₁  N₂  …  N_n  N_n+1  …

строго включенных друг в друга. По лемме Рисса о почти перпендикуляре в каждом N_n найдется элемент z_n та­кой, что ||z_n||= 1 и ||x - z_n||  1/2 для всех x  N_{n – 1}, n = 2,3, ... Рассмотрим последовательность {Az_n}. Она компактна, ибо А вполне непрерывен, а {z_n} ограничена. С другой стороны, при m > n

||Az_m – Az_n|| = ||[z_n – (I – A)z_n + (I – A)z_m] – z_m||  ½,

ибо

z_n - (I- A)z_n + (I - A)z_m  N_{m - 1}

так как

(I – A)^{m - 1} [z_n - (I- A)z_n + (I - A)z_m] = (I – A)^{m - 1}z_n - (I- A)^mz_n + (I - A)^mz_m] = 0

(все слагаемые – нули, ибо (I – A)^kz_i = 0 при k i. Итак, с одной стороны, {Az_n} компактна, а с другой ||Az_m – Az_n|| > 1/2. Полученное противоречие показывает, что допущение N(I - А){0} неверно. I доказано.

II. b)  c) Дано N(I - А) = {0}. Нужно доказать, что R(I– А*) = Х*. Возьмем любой f  Х* и рассмотрим выражение f((I – А)х). Оно определяет линейный ограниченный функционал  X*. Действительно, это выражение определено на X, линейно по х и ограничено. Наконец, самое важное, оно однозначно по х: если f((I - А)х) = f((I - A)х"), то f((I – А) (х' – х")) = 0, откуда, вследствие произвольности f, (I - A) (х' – х") = 0, но N(I - A) = {0}, и, значит, х' = х". Таким образом, f((I - А)х) = (х), т. е. всякий f  X* при­надлежит также и R((I – А*)), т. е. c) доказано.

III. c)  d). Эта часть доказательства совпадает с I. Нужно лишь в I A заменить на А*.

IV. d)  а). Дано N((I – А)*) = {0}. Надо доказать, что R(I – А) = Х. Допустим противное, что R(I – A)  Х. По только, что доказанной теореме R(I – А) – подпространство в X. Пусть у₀  Х и у₀  R(I - А). По следствию из теоремы Хана–Банаха най­дется f₀  X* такой, что f₀₍у₀) = 1, и f₀(у) = 0 для всех y R(I – А). Но тогда f₀((I - А)х) = 0 для всех х Х, или х, (I - А)*f₀ = 0 и из произвольности х имеем (I - A)*f₀ = 0, т.е. f₀N((I - A)*) и f₀  0. Полученное противоречие пока­зывает, что верно а).

V. Если выполнено одно из условий а), b), c). d), то по I–IV выполнены и все остальные, но тогда_; N((I - A)) = {0}, т.е. I - A обратим; R(I - A) = X, и, значит, по теореме Банаха об обратном операторе I - A непрерывно обратим. То же для А*. Теорема полностью доказана.

Теорема 6 (вторая теорема Фредгольма). Пусть А – ли­нейный вполне непрерывный оператор в X. Тогда уравнения (4) и (4*) имеют одинаковое конечное число линейно независимых решений.

Доказательство. Мы уже видели, что если N(I - A) = {0}, то и N((I - А)*) = {0}, и наоборот (1 теорема Фредгольма). Пусть теперь эти подпространства не нулевые. Докажем сна­чала их конечномерность. Пусть М – произвольное ограничен­ное множество, лежащее в N(I – A); тогда М = AM. Отсюда М компактно. Получилось, что в N(I - A) каждое ограниченное множество компактно. По теореме Рисса о локальной компактности N(I – A) конечномерно. Аналогично, дело обстоит N((I – A)*).

Перейдем к доказательству равенства dimN(I - A) = dim(I - А)* размерностей подпространств нулей операторов (I – A) и (I – A)*. Допустим противное, что, например,

dim N (I - А) = n < m = dim N((I - A)*).

Пусть {_i}₁ⁿ базис в N(I – А). По следствию из теоремы Хана – Банаха существует система функционалов {g_i}₁ⁿ  X*: g_i(_j) = _ij (биортогональная система) i, j = 1, ..., n. Пусть, далее, {_i}₁ⁿ – базис в N((I – А)*), а {z_i}₁ⁿ  X – биортогональная к нему система элементов: _i(z_j) = _ij, i, j = 1, 2, ..., n. Рассмотрим оператор I – В, где

(5)

Оператор В вполне непрерывен, как сумма двух вполне непре­рывных операторов – оператора А и конечномерного оператора.

Далее, докажем, что N(I - В) = {0}. Действительно, уравнение х – Вх = 0 записывается согласно (5) так:

(6)

Применяя к обеим его частям функционал _k, получим

(6)

Мы воспользовались тем, что _k N((I – А)*), и биортогональ­ностью систем {_i} и {z_i}. Так как k произвольно, то все g_k(х) = 0 и (5) принимает вид х – Ах = 0. Это означает, что xN(I - A), т. е.

(7)

Применим к обеим частям этого равенства функционал g_i и, пользуясь биортогональностью систем {_i}, {g_i} и тем, что g_i(x) = 0, получим _i = 0. Так как i произвольно, то х = 0. Итак, N(I - В) = {0}.

Нетрудно убедиться (проверьте!), что

.

Тогда (I – В)*_s = (I – A*)_s - = 0 при s > n, ибо_s  N((I - В)*), и z_i, _s = 0, при n < s. Оказалось, что N((I – В)*)  {0}, а это противоречит теореме 2. Следователь­но, предположение п < m неверно. Аналогичное доказательство проводится в случае п > m с заменой A на A*. Теорема дока­зана.

Теорема 7 (третья теорема Фредгольма). Пусть А – ли­нейный вполне непрерывный оператор в X. Для того, чтобы уравнение (3) имело хоть одно решение, необходимо и доста­точно, чтобы для любого решения  уравнения (4*) выполня­лось условие у,  = 0.

Доказательство. Если N(I - A) = {0}, то N((I - A)*) = {0} и утверждение теоремы тривиально. Пусть N(I - A)  {0}. Если уравнение (3) имеет решение х₀, то для всякого N((I - А)*) имеем

у,  = (I - А) х₀,  = х₀, (I – A)* = 0.

Обратно, пусть у,  = 0 для всех N((I - А)*). Допу­стим, что (3) при данном у решений не имеет, т. е. уR(I - А). Заметим, что R(A) замкнуто по теореме о замкнутости области значений непрерывного оператора. По следствию из теоремы Хана – Банаха существует f X* такой, что f(y) = 1 и f((I - А)х) = 0 для любых хХ, но тогда x, (I - A)*f = 0 и, вследствие произвольности х, (I - A)*f = 0, т. е. fN((I - A)*). Но тогда по условию теоремы f(у) = 0  1. Получен­ное противоречие означает, что уравнение (3) разрешимо. Тео­рема доказана.

В заключение кратко резюмируем полученные результаты. Для уравнения (3) с вполне непрерывным оператором A воз­можны только три следующие ситуации:

1) оператор I – А непрерывно обратим, тогда (3) имеет при любой правой части у единственное решение х = (I – А)^-1у;

2) N(I – А)  {0}; если у,   0 хоть для одного решения  сопряженного однородного уравнения (4*), то (3) решений не имеет;

3) N(I – А)  {0}; если у,  = 0 для всех решений  урав­нения (4*), то общее решение уравнения (3) имеет вид х = х_о - , где x₀ – частное решение (3), {_i}– базис под­пространства решений уравнения (4), аn –размерность этого подпространства.

4. Резольвента и спектр оператора. Линейная независимость собственных векторов. Спектр вполне непрерывного оператора (конечномерность собственного подпространства, конечное число собственных значений вне круга)

Часто вместо уравнений (3) приходится рассматривать уравнения

(8)

где ,х – искомый, у – известный элемент, а  – некоторый числовой параметр. Уравнение (8) можно также записать в виде

(8*)

Одновременно с уравнением (8) целесообразно рассматривать уравнение

(9)

которое, называют однородным уравнением, соответствующим уравнению (8). Уравнение же (8) называют тогда неоднород­ным. Ясно, что однородное уравнение всегда имеет нулевое решение x = 0.

Пусть оператор для данного значения пара­метраимеет обратный операторэтот оператор называютразрешающим оператором или резольвентой для уравнения (8) или оператора А и обо­значают . Тогда уравнение (8) при любом имеет решение и притом только одно. Однородное уравнение (9) имеет в этом случае лишь нулевое решение. Такие значения параметра называются регулярными значениями оператора А или уравнения (8). Множество значений параметра , не являющиеся регулярными, называются спектром оператора А. Может случиться, что однородное уравнение (9), кроме нулевого, имеет еще одно или несколько ре­шений, отличных от нуля. Такие значения параметра, при которых это происходит, называются характеристическими числами или собственными значе­ниями оператора А. Так как в этом случае решение урав­нения (9), являющегося частным случаем уравнения (8), не однозначно, то собственные значения принадлежат спектру. Однако могут существовать точки спектра, не являющиеся собственными значениями.

В 7 главе (теорема 7) рассматривался вопрос обратимости оператора . В этом случае обратный оператор не является, строго говоря, резольвентой оператораА. Однако с помощью этого оператора резольвенту можно по­лучить без труда. В самом деле, преобразуем оператор следующим образом:

где Если теперьтои поэтому существует. Но тогда т.е. Таким образом, резольвента представима в виде сходящегося в области ряда

=

Пример 1. Рассмотрим в пространстве С [0, 1] опе­ратор умножения на независимое переменное Уравнение (8) принимает в этом случае

(10)

и решение x(t) этого уравнения есть функция, тождественно ему удовлетворяющая. Если лежит вне отрезка [0, 1], то уравнение (10) имеет при любому (t) единственное непрерывное решение

откуда следует, что все такие значения параметра являются регулярными, и резольвента есть оператор умножения на

Все значения параметра, принадлежащие отрезку [0, 1], являются точками спектра. В самом деле, пусть . Возьмем в качествеy(t) какую-нибудь функцию, не обращающуюся в нуль в точке Для такой функции равенствоне может тождественно удовлетворяться ни при какой непрерывной на отрезке [0, 1] функциих (t), ибо в точке левая часть его равна нулю, в то время как правая отлична от нуля. Следовательно, приуравнение (10) не имеет решения для произвольной правой части, что и доказывает принадлежностьспектру оператораА, Вместе с тем ни одна точка спектра не является собственным значением, так как решение однородного уравнения при любомt, отличном от, а следовательно, в силу непрерывности и приобращается в нуль, т.е. тождественно равно нулю.

Пример 2. Положим Х = Y = R_n и пусть оператор А задается квадратной матрицей Уравнение (4) примет для вид

(11)

Это есть система линейных неоднородных алгебраических уравнений. Если определитель системы

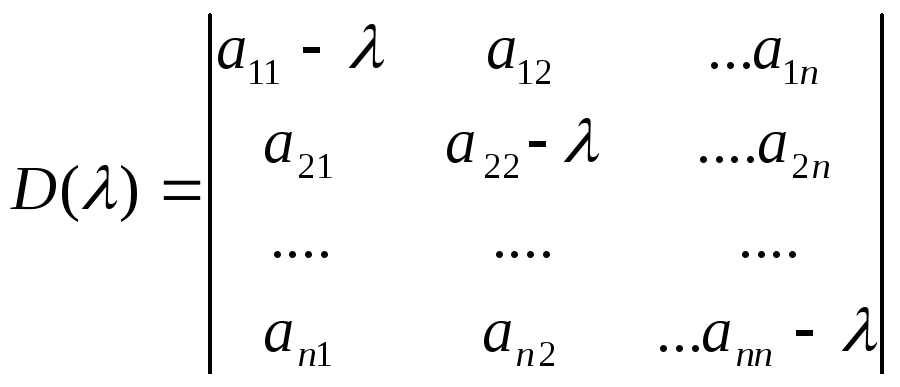
отличен от нуля, т. е. если не есть корень уравнения, то система уравнений (11) имеет при любых правых частях единственное решение, и следовательно, все такие значения параметра  регулярны. Корни уравнения D() = 0 образуют спектр, так как при таких  система (11) в общем случае не­разрешима. Однако при этих значениях параметра однород­ная система

имеет нетривиальное решение (т. е. отличное от нулевого), и, следовательно, любая точка спектра есть собственное зна­чение.

В приведённых примерах спектр оператора либо не со­держал, ни одного собственного значения, либо состоял только, из собственных значений. Имеются примеры, где спектр оператора содержит как собственные значения, так и точки, не являющиеся собственными значёниями.

Лемма 5. Собственные векторы симметрического оператора, отвечающие различным собственным значениям, взаимно ортогональны.

Доказательство. Действительно, пусть имеют место равенства

и .

Умножим первое равенство скалярно на , второе наи вычитая второе из первого, получим

Левая часть равенства равна нулю вследствие симметрии оператора А. Так как , тоЛемма 5 доказана.

Лемма 6. У вполне непрерывного оператора А всякая ортогональная нормированная система собственных векторов с собственными значениями, превосходящими по модулю положительное значение , конечна.

Доказательство. Допустим, что нашлась бесконечная система таких собственных векторов. Каждый из них операторомпереводится в себя самого с числовым множителем, по модулю большим числа. Пусть и- какие-то два из этих собственных векторов:

Имеем

Это означает, что расстояние между векторами, полученными после воздействия оператора на вектора системы, заведомо будут превосходитьНо из совокупности таких векторов нельзя выбрать никакой сходящейся последовательности, что противоречит полной непрерывности оператора. Лемма 6 доказана.

Следствие. Существует только конечное число взаимно ортогональных векторов с данным собственным значением иными словами, каждое собственное подпространство, отвечающее ненулевому собственному значению( т.е. совокупность всех собственных векторов оператораА с фиксированным собственным значением . Это множество очевидно, есть (замкнутое) подпространство в Н) вполне непрерывного симметричного оператора конечномерно.

5. Существование собственного значения у вполне непрерывного оператора в гильбертовом пространстве. Наибольшее и наименьшее собственные значения. Спектральное разложение самосопряженных операторов. Теорема Гильберта-Шмидта о разложении по собственным векторам

Мы переходим теперь к фундаментальной теореме о симметричных вполне непрерывных операторах.

Теорема 8. (Гильберта-Шмидта). В гильбертовом сепарабельном пространстве всякий симметричный вполне непрерывный оператор обладает полной ортогональной системой собственных векторов.

Доказательство этой теоремы проведём в несколько этапов.

Лемма 7. Если и А– симметричный оператор, то

причем знак равенства возможен только в случае, когда е есть собственный вектор оператора с собственным значением

Доказательство. В силу симметрии оператора и неравенства Коши – Буняковского имеем:

(12)

Неравенство Коши – Буняковского обращается в равенство, лишь когда фигурирующие в нём векторы коллинеарные, поэтому в случае равенства имеем т.е. есть собственный вектор оператораА². Подставляя полученное выражение в (12), находим :

Лемма доказана.

Назовем максимальным вектором ограниченного оператора А такой единичный вектор на котором величинадостигает своего наибольшего значенияВообще говоря, не у всякого ограниченного оператора существует максимальный вектор.

Лемма 8. Симметричный вполне непрерывный оператор обладает максимальным вектором.

Доказательство. Выберем последовательность , гдетак, чтобы иметьИз последовательностиможно выделить в силу полной непрерывности А, сходящуюся подпоследовательность, удалив лишние векторы и исправив нумерацию, можно считать, что сама последовательностьсходится при; пустьВ силу непрерывности нормыПокажем, что векторявляется исходным максимальным вектором. Прежде всего, в силу непрерывности оператораА имеем:

Векторы принадлежат единичному шару, и поэтому векторыпо длине не превосходят. Применяя лемму 7, получаем:

.

Откуда вытекает, что

т.е. есть максимальный вектор оператораА. Лемма доказана.

Лемма 9. Если есть максимальный вектор для симметричного оператора, тоявляется собственным вектором для операторас собственным значением

Доказательство. По лемме 7 и по определению нормы оператора имеем:

откуда следует, что

В силу леммы 7 вектор есть собственный вектор операторас собственным значениемЛемма доказана.

Лемма 10. Если оператор обладает собственным вектором с собственным значением, то операторА имеет собственный вектор с собственным значением или

Доказательство. Равенство можно записать в виде

Допустим, что . Тогда из условияили, что тоже,вытекает, чтоесть собственный вектор операторас собственным значениемЕсли же, тои тогда векторесть собственный вектор оператораА собственным значением Лемма доказана.

Леммы 7-10 показывают, что всякий симметричный вполне непрерывный оператор А обладает собственным вектором с собственным значением Покажем теперь, что из собственных векторов оператораА можно построить ортогональную систему в пространстве Н.

Лемма 6 позволяет сделать определённые выводы относительно совокупности всех собственных векторов и собственных значений оператора А. Рассмотрим на вещественной оси множество всех собственных значений оператора А. В силу леммы 6, существует лишь конечное число собственных значений, превосходящих по абсолютной величине данное положительное число , поэтому, если собственных значений бесконечное (очевидно, счётное) множество, то они образуют последовательность, сходящуюся к нулю. Следовательно, мы можем занумеровать натуральными числами все собственные значения в порядке убывания абсолютной величины. Условимся, что при этом мы будем каждое собственное значение снабжать столькими последовательными номерами, какова размерность соответствующего собственного подпространства (эта размерность называетсякратностью этого собственного значения). В таком случае последовательность ненулевых собственных значений оператора А

мы можем сопоставить последовательность собственных векторов причёмМожно считать, что векторывзаимно ортогональны и нормированы. В самом деле, еслито ортогональностьвыполняется в силу леммы 5; если жето в пределах конечного собственного подпространства, отвечающего собственному значениюмы всегда можем провести ортогонализацию. Нормировка всех полученных векторов завершает построение.

Покажем теперь, что каждый вектор , ортогональный всем построенным векторампереводится операторомА в нуль.

Лемма 11. Пусть – подпространство в гильбертовом пространстве Н, инвариантное относительно симметричного оператора А (т.е. каждый вектор подпространства переводится операторомА в вектор этого же пространства). Тогда ортогональное дополнение подпространстватакже инвариантно относительно оператораА.

Доказательство. Пусть – любой вектор из подпространства ,– любой вектор из подпространства . По условиюТогда в силу симметрии оператораА следует, что Это означает, что векторортогонален любому векторуи, следовательно,Лемма доказана.

Теперь рассмотрим совокупность Р всех векторов ортогональных всем построенным векторамЭто совокупностьР является замкнутым подпространством как ортогональное дополнение к подпространству L, порождённому ортогональной системой ПосколькуL, очевидно, инвариантно относительно оператора А, то его ортогональное дополнение P (по лемме 11) также инвариантно относительно оператора A. Обозначим через M(P) точную верхнюю границу значений на единичной сфере подпространстваP. В силу лемм 9 и 10, в подпространстве Р имеется собственный вектор с собственным значениемНо по самому построению подпространстваР оно не может содержать ни одного собственного вектора с ненулевым собственным значением. Отсюда ; но это означает, чтодля любого векторачто и требовалось доказать.

Каждый вектор может быть представлен в виде суммы

Вектор у можно далее разложить в ряд Фурье по системе полной в пространствеL; вектор z, по доказанному, оператором A переводится в нулевой вектор. Мы получили следующую основную теорему:

Терема 9. В гильбертовом пространстве , в котором задан симметричный вполне непрерывный операторA, каждый вектор может быть представлен в виде ортогональной суммыгде(конечная или бесконечная) система собственных векторов операторас ненулевыми собственными значениями и

Из этой теоремы вытекает и теорема Гильберта. Действительно, в сепарабельном гильбертовом пространстве H подпространство P также сепарабельно и в нём можно выбрать полную ортогональную систему вместе с уже построенными векторамиполучается полная ортогональная система в всём пространствеH. Каждый из векторов этой системы является собственным вектором оператора A: векторы с собственнымиа векторыс собственным значением 0. Тем самым теорема Гильберта доказана.

Из теоремы Гильберта следует, что т.е. любой вектор, где, допускает разложение по собственным векторам операторас ненулевыми собственными значениями.

Задачи

1. Доказать следующие утверждения:

А) любой линейный оператор A: RⁿR^m вполне непрерывен;

Б) любой линейный оператор A: E₁E₂ вполне непрерывен, если E₁ – конечномерное пространство;

В) любой ограниченный линейный оператор A: E₁E₂ вполне непрерывен, если E₂ – конечномерное пространство;

Г) линейный ограниченный оператор, образ которого лежит в конечномерном пространстве, вполне непрерывен.

2. Являются ли вполне непрерывными следующие операторы в пространстве C[0, 1]? В пространстве L²[0, 1]?

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

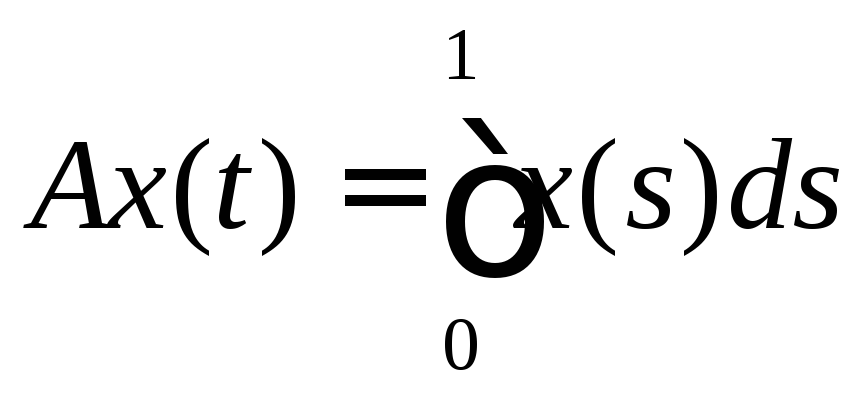10. Ax(t)=x(t²).

3. Имеет ли оператор собственные значения в пространстве?

4. Показать, что для уравнения , где– оператор Вольтерра, а непрерывно для, все значения параметрарегулярны.

Показать, что если значение параметра  является регулярным для оператора, то оно будет регулярным и для оператора А + В, когда достаточно мала.

5. Показать, что всякий вполне непрерывный оператор в сепарабельном гильбертовом пространстве Н есть предел операторов, отображающих все пространство на конечномерное подпространство.

Указание: можно считать, что . Если, то положим.

6. Показать, что оператор А в сепарабельном гильбертовом пространстве, заданный в ортонормальном базисе матрицейпо формуламвполне непрерывен, если

Указание: смотри задачу 5.

7. Положим для ,,. Какие из этих операторов вполне непрерывны?

8. Для , положим, показать, чтоА – вполне непрерывный оператор.

9. Каковы собственные функции интегрального оператора Фредгольма с ядром в промежутках а), б)?

10. Решить уравнение .

11. В пространстве C[0, 1] рассмотрим оператор

.

Найти спектр и резольвенту оператора А.

12. В вещественном линейном пространстве C[-, ] найти собственные значения и собственные вектора операторов

а) (Ax)(t) = x(-t);

b) .

Имеют ли в этом пространстве данные операторы непрерывный спектр? Построить резольвенты на множестве регулярных значений каждого оператора.

13. В комплексном пространстве C[0, 1] рассмотрим оператор (Ах)(t) = x(0) + tx(1). Найти точечный и непрерывный спектры оператора А и построить резольвенту на множестве регулярных значений.

14. В пространстве C[0, 2] рассмотрим оператор (Ах)(t) = e^ittx(t). Доказать, что спектр оператора А есть множество { C: || = 1}, причем ни одна точка спектра не является собственным числом.

15. Найти спектр и резольвенту оператора А в пространстве L₂[-1, 1]

.

16. Какой должна быть функция С[a, b], чтобы оператор умножения А: С[a, b]  С[a, b], определенный с помощью равенства (Ах)(t) = (t)x(t) был вполне непрерывным.

17. Найти спектр и собственные значения оператора умножения на фиксированную непрерывную функцию в пространстве C[a, b].

18. Найти спектр оператора А в пространстве L₂(R):

.

19. Пусть число p > 1 и q – ему сопряженное, т.е. 1/p + 1/q = 1. Рассмотрим оператор А: l_p  l_q, который определяется формулой

,

где числовая матрица такая, что двойной рядсходится. Доказать, что операторА вполне непрерывен.

20. Рассмотрим оператор А: l_p  l_q, который определяется формулой

Ах = (₁х₁, ₂х₂, …), х = (х₁, х₂, …)

где _k – заданная последовательность чисел, k =1, 2, … Какова должна быть последовательность этих чисел, чтобы оператор А был вполне непрерывен.

21. Пусть в гильбертовом пространстве Н задан линейный ограниченный оператор А такой, что А*А является вполне непрерывным оператором в Н. Доказать, что оператор А вполне непрерывен?