
- •Введение
- •Глава 1 топологические пространства
- •1. Понятие множества. Операции над множествами. Отображения. Характеристическая функция множества
- •2. Топология и топологическое пространство. База топологии
- •3. Структура открытых множеств и окрестности
- •4. Понятие метрического пространства и топологии, определяемой метрикой. Примеры метрических пространств
- •5. Операция замыкания множества в топологическом пространстве
- •6. Внутренние точки множества, внутренность. Граница множества
- •7. Сепарабельные топологические пространства
- •8. Индуцированные топологии и фактортопология
- •9. Непрерывное отображение. Гомеоморфизм
- •10. Компактные пространства
- •Глава 2 свойства метрических пространств
- •1. Сходящиеся последовательности в метрических пространствах и полные метрические пространства
- •2. Теорема о пополнении метрического пространства
- •3. Критерий полноты пространства
- •4. Компактные множества в метрическом пространстве. Теорема Хаусдорфа
- •5. Критерии компактности в пространствах с[0, 1], lp. Теорема Арцела
- •6. Теорема Вейерштрасса о равномерном приближении и сепарабельность с[0, 1]
- •7. Отображение компактных множеств. Теорема Вейерштраса об ограниченности и достижении точных граней непрерывной функцией
- •8. Принцип сжимающих отображений и его применение
- •9. Нигде не плотные множества. Понятие категории множеств метрического пространства. Теорема Бэра
- •Глава 3 мера и измеримые множества
- •1. Системы множеств
- •2. Системы множеств в евклидовом пространстве
- •3. Функция множеств
- •4. Мера и ее простейшие свойства. Мера в евклидовом пространстве
- •5. Внешняя мера
- •6. Измеримые множества
- •7. Мера Лебега на Rn
- •Глава 4 измеримые функции
- •1. Измеримые функции и их свойства
- •2. Сходимость почти всюду
- •3. Сходимость по мере и ее свойства
- •4. Сравнение сходимости почти всюду и по мере
- •5. Почти равномерная сходимость. Теоремы Егорова и Лузина
- •Глава 5 интеграл лебега
- •1. Интеграл Лебега для простых и ограниченных функций на пространстве с конечной мерой
- •2. Основные свойства интеграла от ограниченной функции
- •3. Определение интеграла Лебега в произвольном случае
- •4. Предельный переход под знаком интеграла
- •5. Сравнение интегралов Римана и Лебега
- •6. Заряды. Теорема Радона—Никодима
- •Глава 6 нормированные и гильбертовы пространства
- •2. Конечномерные пространства. Конечномерность и компактность. Теорема Рисса о локальной компактности.
- •3. Скалярное произведение. Гильбертово пространство. Аксиомы и свойства. Ортонормированные системы. Ортогонализация по Шмидту. Тождество параллелограмма.
- •4. Ортогональность и ортогональное дополнение
- •5. Ряды Фурье в гильбертовом пространстве. Коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля. Полные и замкнутые ортонормированные системы
- •Глава 7 линейные операторы в нормированных пространствах
- •2. Пространство линейных непрерывных операторов и его полнота относительно равномерной сходимости операторов
- •3. Принцип равномерной ограниченности и теорема Банаха-Штейнгауза. Полнота пространства операторов относительно поточечной сходимости
- •4. Ядро оператора. Критерий ограниченности обратного оператора. Теоремы об обратном операторе
- •5. Примеры обратных операторов. Обратимость операторов вида (I - a) и (a - c).
- •6. График оператора и замкнутые операторы. Критерий замкнутости. Теорема Банаха о замкнутом графике. Теорема об открытом отображении
- •Xn(t)X(t) равномерно на [a, b],.
- •X'n(t) y(t) равномерно на [а, b].
- •Глава 8 линейные функционалы в нормированных пространствах
- •1. Линейные непрерывные функционалы. Продолжение по непрерывности. Теорема Хана-Банаха. Следствия из теоремы Хана-Банаха
- •2. Сопряженные пространства
- •3. Теорема Рисса об общем виде линейного функционала для пространства непрерывных функций
- •4. Пространства Лебега и сопряженные к ним
- •5. Изоморфизм и изометрия сепарабельных гильбертовых пространств. Общий вид линейного функционала в гильбертовом пространстве. Теорема Рисса-Фишера.
- •6. Сопряженный оператор. Условия существования сопряженного оператора. Замкнутость сопряженного оператора. Сопряженный оператор к ограниченному оператору и его норма.
- •7. Самосопряженный оператор. Норма самосопряженного оператора
- •Глава 9 спектральная теория операторов
- •1. Вполне непрерывные операторы и их свойства. Операторы Фредгольма и Гильберта-Шмидта
- •2. Теорема Шаудера о полной непрерывности сопряженного оператора. Уравнения первого и второго рода с вполне непрерывными операторами. Теорема о замкнутости области значений оператора
- •3. Альтернативы Фредгольма. Теорема Шаудера о неподвижной точке.
- •Предметный указатель
7. Самосопряженный оператор. Норма самосопряженного оператора
Определение 4. Линейный ограниченный оператор А в гильбертовом пространстве Н называется самосопряженным или симметрическим, если он совпадает со своим сопряженным: А = А*.
Иными словами,
самосопряженный оператор А
характеризуется условием (Ax,
y)
=
(x,
Ay)
для
![]() .
В последнем примере, если ядроK(t,
s)
симметрическое: K(t,
s)
=
K(s,
t), то
.
В последнем примере, если ядроK(t,
s)
симметрическое: K(t,
s)
=
K(s,
t), то
![]()
и значит, интегральный оператор будет симметрическим.
Нетрудно видеть, что любая линейная комбинация самосопряженных операторов также является самосопряженным оператором.
Таким образом, в
линейном нормированном пространстве
линейных операторов, отображающих Н
в Н,
самосопряженные операторы составляют
линейное многообразие. Кроме того, мы
сейчас докажем, что это подмножество
замкнуто и, следовательно, является
подпространством. Другими словами, если
операторы An
– самосопряженные и An![]() (по норме), то и операторА
– самосопряженный. Докажем даже более
сильное утверждение.
(по норме), то и операторА
– самосопряженный. Докажем даже более
сильное утверждение.
Теорема 13. Если операторы An – самосопряженные и последовательность {An} точечно сходится к оператору А, то А будет также самосопряженный оператор.
Доказательство.
Из непрерывности скалярного произведения
следует, что при любых
![]() .
.
(Ах,
у)
= (![]() Аnx,
y)
=
Аnx,
y)
=
![]() (Аnx,
y) =
(Аnx,
y) =
![]() (x,
Аny)
= (x,
(x,
Аny)
= (x,
![]() Аny)
= (x,
Ay).
Аny)
= (x,
Ay).
Теорема доказана.
Если операторы А
и В
– самосопряжённые, то
![]() Следовательно, для того, чтобы операторАВ
был самосопряжённым, необходимо и
достаточно, чтобы
Следовательно, для того, чтобы операторАВ
был самосопряжённым, необходимо и
достаточно, чтобы
![]() ,
т.е., чтобы операторыА
и В
были перестановочны между собой. В
частности, все степени
,
т.е., чтобы операторыА
и В
были перестановочны между собой. В
частности, все степени
![]() самосопряжённого оператораА
также есть самосопряжённые операторы.
самосопряжённого оператораА
также есть самосопряжённые операторы.
Имеет место следующая важная формула для нормы самосопряжённого оператора.
Теорема 14. Если оператор А – самосопряжённый, то
![]()
Доказательство.
По неравенству Коши – Буняковского
имеем, при
![]()
![]() Следовательно, если
Следовательно, если![]() то
то![]()
Докажем обратное
неравенство. Заметим, что любой
![]() можно
представит в виде
можно
представит в виде![]() где
где![]() (т.к. если
(т.к. если![]() то
то если
если![]() то
то![]() любой
вектор с нормой равной единице). Отсюда
для любого
любой
вектор с нормой равной единице). Отсюда
для любого![]() выполнено |(Az,
z)| = ||z||2|(Az,
z
)|
C||z||2.
выполнено |(Az,
z)| = ||z||2|(Az,
z
)|
C||z||2.
Теперь для любых
![]() учитывая
равенство
учитывая
равенство![]() имеем
имеем
![]()
![]()
и, вычитая из первого равенства второе, находим
![]()
Отсюда, и установленного выше неравенства |(Az, z)| C||z||2
|(Ax,
y)|
![]() C(||x
+ y||2
+ ||x
– y||2)|.
C(||x
+ y||2
+ ||x
– y||2)|.
Воспользуемся равенством параллелограмма (теорема 6.8)
![]() ,
,
получаем
|(Ax,
y)|
![]() C(||x||2
+ ||y||2)|.
C(||x||2
+ ||y||2)|.
Полагая
![]() подставим в последнем неравенстве
подставим в последнем неравенстве .
Тогда
.
Тогда![]() и
мы получаем
и
мы получаем или
или![]() Это же неравенство верно и приАх
= 0. Следовательно,
Это же неравенство верно и приАх
= 0. Следовательно,
![]() и, тем самым, равенство
и, тем самым, равенство![]() доказано.
доказано.
Следствие 1.
Если для
самосопряжённого оператора
![]() при всех
при всех![]() тоА=0.
тоА=0.
Действительно,
если
![]() при
всех
при
всех![]() то
по теореме,
то
по теореме,![]() и значитА
= 0.
и значитА
= 0.
Для самосопряжённого оператора А вводится ещё понятие его границ – верхней и нижней:
![]()
Следствие 2.![]() Из
теоремы следует, что
Из
теоремы следует, что
![]()
Из определения
границ легко выводится, что для любого
![]() имеет
место соотношение
имеет
место соотношение
![]()
Задачи
1. Являются ли линейными следующие функционалы в C[0, 1]?
 ;
;F(x)=x(1/2);
 ;
;
 ;
; ;
;F(x)=x(t0);
 ;
; ;
; .
.
Какие из этих функционалов непрерывны в C[0, 1]? Вычислить их нормы.
Какие из этих функционалов непрерывны в L2[0,1]? Вычислить их нормы.
2. Какие из указанных функционалов, действующих на соответствующих классах элементов из l2, будут линейными; непрерывными?
f(x)=
 xksink;
xksink;f(x)= xk;
f(x)=
 xksgn(k-n);
xksgn(k-n);f(x)=
 xk2k1/2;
xk2k1/2;f(x)=
 xkk-1/2;
xkk-1/2;f(x)=
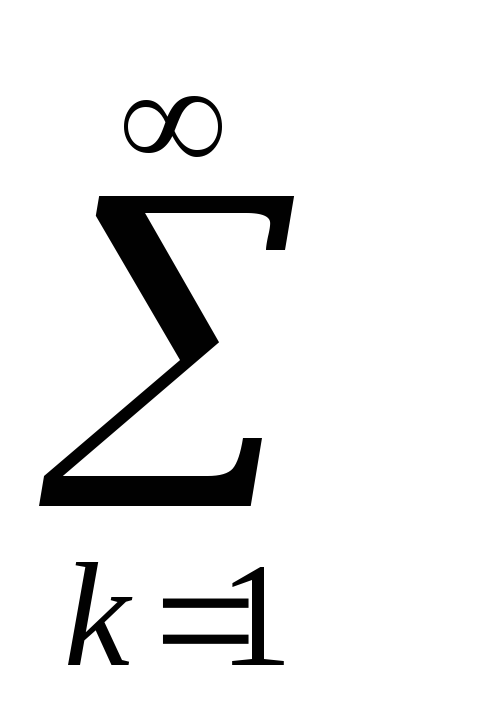 xk2;
xk2;f(x)= xk-xk-1;
f(x)=
 |xk|;
|xk|;f(x)=supk|xk|;
f(x)=
 |xk|
2.
|xk|
2.
3. Найти норму
функционала
 в пространстве C[0, 1].
в пространстве C[0, 1].
4. Непрерывны ли
на пространстве
![]() ,
следующие линейные функционалы
,
следующие линейные функционалы
а)
![]() ;
;
б)
![]() ;
;
5. Проверить, что функционал

непрерывен в
пространстве
![]() ;
показать, что точная верхняя грань его
значений в замкнутом единичном шаре
пространства С[0,1] равна 1, но эта верхняя
грань не достигается ни на каком элементе
единичного шара.
;
показать, что точная верхняя грань его
значений в замкнутом единичном шаре
пространства С[0,1] равна 1, но эта верхняя
грань не достигается ни на каком элементе
единичного шара.
6. Пусть в гильбертовом пространстве последовательность {хn} слабо сходится к х0, т.е. (xn, y) (x0, y) для любого y H, и ||хn|| ||х0||. Показать, что хn х0.
7. Если в гильбертовом пространстве последовательность {хn} слабо сходится к х0 и последовательность {yn} сходится по норме к y0, то (хn, yn) (х0, y0). Достаточно ли слабой сходимости последовательности {yn}?
8. Докажите, что в конечномерном пространстве слабая сходимость совпадает с сильной, т.е. сходимостью по норме.
