4. Пространства Лебега и сопряженные к ним

Пусть задано измеримое пространство (X, , ) с счетно-аддитивной меры  на множестве X и 1  р < .

Определение 2. Множество всех измеримых функ­ций f: X  R, у которых степень |f |^p интегрируема на X, называется лебеговым пространством L_р(Х).

Элементами этого пространства L_р(Х) являются клас­сы эквивалентных функций.

Из неравенства Минковского вытекает, что L_р(Х) является линейным пространством. Норма в этом пространстве определяется по формуле:

.

Теорема 5. Пространства L_р(Х) при 1  р <  являются банаховыми.

Доказательство. Вначале покажем, что L_р(Х) являет­ся нормированным пространством. Однородность нормы очевидно выполнена. Из неравенства Минковского вытекает ||f + g|| < ||f || + ||g|| – неравенство треугольника. Если ||f || = 0, то f(x) = 0 при п. в. х Х (следствие 2 теоремы 5.4), и значит функция f ~ 0 эквивалентна нулю на X. Таким образом, все аксиомы нормы выполнены.

Докажем полноту пространства L_р(Х). Для каждой фундаментальной последовательности {f_n} возьмем по­следовательность индексов n₁ < n₂ < ... так, что при всех i, j  n_k выполняется неравенство ||f_i – f_j|| <2^–k. Теперь заметим, что функция g(x) = ,

,

интегрируема в степени р. В самом деле, функции g_n(x) образуют неубывающую последовательность g_n  g при п   и по неравенству треугольника

.

Следовательно, в силу теоремы о монотонной сходимо­сти функция g будет интегрируемой в степени р и значит конечной п. в. на множестве X. Отсюда ряд

сходится абсолютно п. в. на X. Так как |f(x)|^p  g^p(x), то функция f будет также интегрируемой в степени р.

Применяя лемму Фату (лемма 5.4) и неравенство треугольника, мы получим неравенство

.

Таким образом, = 0, т. е. существует предел у подпоследовательности {}.Осталось заметить, что если последовательность {f_n} фундаментальна в норми­рованном пространстве L_р(Х) и содержит сходящуюся подпоследовательность к функции f, то сама последо­вательность также является сходящейся в пространстве L_р(Х) и ее предел будет равен f (лемма 3.4).

Определение 3. Множество всех измеримых функ­ций f: X  R, ограниченных на дополнении некоторого множества меры нуль, образует пространство L_(X).

Элементами этого пространства L_(X) являются клас­сы эквивалентных функций, называемые существенно ограниченными функциями на множестве X.

Из свойств измеримых функций вытекает, что L_(X) есть линейное пространство. Норма в нем по определению равна существенной верхней грани

.

Докажем, что нижняя грань в определении нормы до­стигается на некотором множестве меры нуль. Для этого выберем множества A_n  меры нуль так, чтобы

,

и положим N(f) = . В силу счетной полуаддитив­ности меры множествоN(f) имеет меру нуль и, значит, справедливо равенство .

Отсюда нетрудно заметить, что сходимость в простран­стве L_(X) совпадает с равномерной сходимостью на до­полнении некоторого множества меры нуль.

Теорема 6. Пространство существенно ограничен­ных функций L_(X) есть банахово пространство.

Доказательство. Докажем вначале, что в пространстве L_(X) выполняются аксиомы нормы. Свойство однород­ности нормы очевидно выполнено. Если ||f || = 0, то из сказанного выше вытекает, что f(x) = 0 п. в. на X и зна­чит функция f эквивалентна нулю.

Проверим неравенство треугольника. Пусть функции f, g  L_(X) и множество A = N(f)N(g), тогда

.

Докажем полноту пространства L_(X). Для этого рас­смотрим фундаментальную последовательность {f _n} и определим множество D = меры (D) = 0. Поскольку имеет место равенство

,

то на множестве X\D последовательность {f _n} будет ограниченной и фундаментальной в чебышевской метри­ке. В силу полноты пространства ограниченных функций M(X\D} существует равномерный предел на множествеX\D. Положим f = 0 на D, тогда функция f ограничена и измерима на множестве X. При этом, в си­лу равномерной сходимости, предел = 0 в метрикеL_(X).

Пусть задано измеримое пространство (X, , ) с счетно-аддитивной мерой . Обозначим через (Х) множество всех простых интегрируемых функций на X и будем предполагать, что Х имеет -конечную меру.

Теорема 7. Сопряженное пространство L_р*(X) изометрично пространству L_q(X), где число q = p/(p—1) в случае 1 < р <  и q =  в случае р = 1. При этом каждый ограниченный функционал  L_р*(X) пред­ставляется интегралом Лебега:

,

где g  L_q(X) и норма функционала равна |||| = ||g||_q (норме функции g в пространстве L_q(X)).

Доказательство. Рассмотрим функцию (А) = (_А) из­меримого множества А  конечной меры. В силу свой­ства линейности функционала  эта функция является конечно-аддитивной. Поскольку по определению нормы функционала а имеет место неравенство |(A)| = |(_A)|  ||||||_A|| = ||||^1/p(A), то функция (А) – абсолютно непрерывна. По теореме Радона-Никодима существует интегрируемая функция g на каждом измеримом множестве А  конечной меры такая, что имеет место равенство (А) = .

Каждая простая функция h (Х) является линей­ной комбинацией характеристических функций. Поэтому в силу линейности интеграла и функционала 

h (Х).

Возьмем теперь простую функцию h (Х) такую, что 0  h  |g|. Так как функция h^q–1sgn(g(x)) измерима и огра­ничена, то она является равномерным пределом последо­вательности простых функций h_n (Х). Поэтому

= .

Откуда и из определения интеграла Лебега вытекает, что ||g||_q  |||| в случае р > 1.

В случае р = 1 допустим, что при некотором  > 0 мно­жество Е {xA: |g(x)| > |||| + } имеет конечную и положительную меру. Полагая h(х) = _E sgn(g(x)), имеем

.

Это противоречит определению нормы функционала . Следовательно, ||g||_  |||| в случае р = 1.

Поскольку каждая интегрируемая функция f L_p(X) может быть представлена в виде предела простых ин­тегрируемых функций h_n (Х) и в силу неравенства Гельдера мы получим

,

то из непрерывности функционала  вытекает

(f ) = –

указанное представление. Применяя теперь к этому пред­ставлению неравенство Гельдера

,

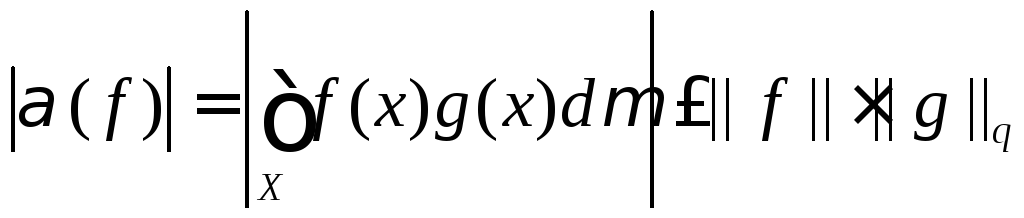заключаем, что норма функционала |||| = ||g||_q.

Пример 7. Пусть 1  р <  и l_р пространство всех последовательностей из примера 6.3. Заметим, что l_р есть частный случай пространства L_p(X), где X = N есть множество натуральных чисел и мера (А) равна количеству натуральных чисел множества А  N.

По доказанному ранее l_p является банаховым простран­ством. Следующая теорема есть частный случай теоремы для пространства L_p(X).

Теорема 8. Если 1  р < , то сопряженное пространство (l_p)* изометрично пространству l_q, где число q = р/(р – 1) в случае 1 < р <  и q =  в случае р = 1.