3. Теорема Рисса об общем виде линейного функционала для пространства непрерывных функций

Рассмотрим пространство C[a,b] непрерывных вещественных функ­ций на отрезке [a,b], которое имеет чебышевскую норму

.

Наша цель описать сопряженное пространство к С[а, b].

Пусть на отрезке [а, b] задана конечная вещественная функция f (x). Разложим отрезок [а, b] на части точками x₀ = a < x₁ < …< x_n = b и составим сумму

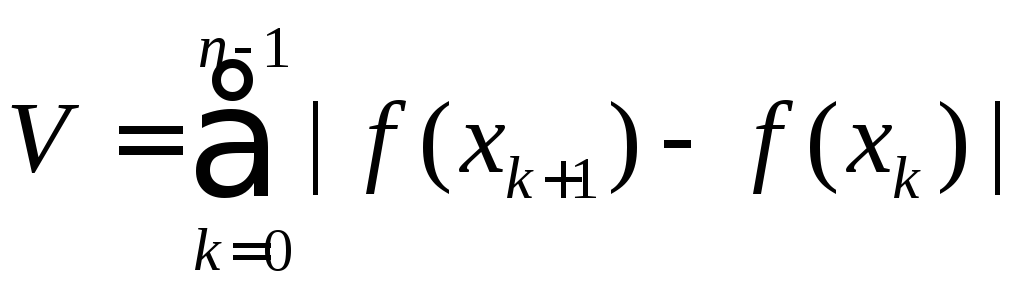
Определение 1. Точная верхняя грань всевозможных сумм V называется полной вариацией функции f (x) на отрезке [а, b] и обозначается . Если полная вариацииf (x) конечна, то функция называется функцией ограниченной вариации.

Пусть далее V[а, b] обозначает пространство всех вещественных функ­ций g: [a, b]  R ограниченной вариации на отрезке [a, b]. В этом пространстве – полная вариация функцииg является полунормой (см. теорему Хана-Банаха):

Считая две функции f, g  V[а, b] эквивалентными f  g, если их разность f(x) – g(x) = с есть константа, получим нормированное пространство, в котором нормой является полная вариация ||g|| = функцииg V[a, b].

Так как любая непрерывная слева функция g(x) ограниченной вариации определяет заряд (задача 5.24) и справедливо разложение Жордана для зарядов (определение 5.7), то с помощью мер, порождаемых этим разложением можно построить интегралы Лебега, разность которых называется интегралом Лебега-Стильтьеса и обозначается

Теорема 4 (Рисса). Для любого ограниченного линейного функ­ционала С*[а, b] найдется такая функция ограни­ченной вариации g V[a, b], что функционал представ­ляется в виде интеграла Лебега-Стилтьеса:

и его норма равна вариации |||| = функции g.

Доказательство. Пространство непрерывных функций есть замкнутое подпространство в пространстве M[a, b] ограниченных функций на отрезке [a, b].

По следствию из теоремы Хана-Банаха каждый функ­ционал С*[а, b], определенный на подпространстве С[а, b], имеет продолжение на все пространство M[a, b] с сохранением его нормы. Это продолжение мы будем обозначать также через а.

Пусть u_t(x) = _{[a, t)}(x) – характеристическая функция полуинтервала [a, t), если а  t < 1, и функция и_b(х) = 1 на отрезке [a, b]. Покажем, что функция g(t) = (u_t) имеет ограниченную вариацию на [a, b]. Действительно, для данного разбиения  отрезка [a, b], оценим сумму

=

=,

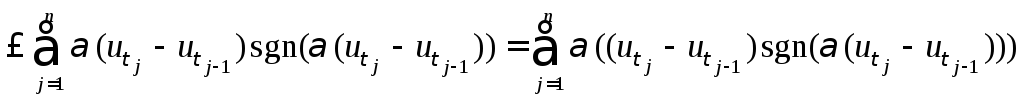где последнее неравенство вытекает из определения нор­мы функционала. Так как функция на отрезке принимает лишь два значения, либо +1 , либо -1, то= 1 и мы получили неравенство ||||. Отсюда  |||| и, следовательно, величина вариа­ции функции g будет конечной на отрезке [a, b].

Возьмем теперь произвольную непрерывную функцию f  С[a, b] и построим ступенчатую функцию

,

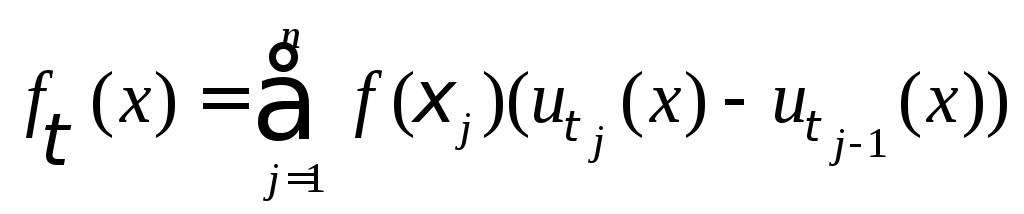где _j [_{j – 1}, _j]. Пусть d_ = maх(_j - _{j - 1}) – диаметр разбиения. Тогда для любой последовательности разбиений с d_  0 после­довательность функций f_ сходится равномерно к f на отрезке [a, b] и в силу непрерывности функционала (f ) получим, что предел равен интегралу Стилтьеса

.

Таким образом, каждый ограниченный функционал  из сопряженного пространства C*[a,b] представляется ин­тегралом Стилтьеса относительно функции g(t) = (u_t) ограниченной вариации на отрезке [a, b] и теорема доказана.

Нетрудно показать, что для любой функции ограниченной вариации, выражение из теоремы 3 определяет линейный непрерывный функционал. Можно также установить, что пространство C*[a,b] изометрически изоморфно пространству функций ограниченной вариации, непрерывных слева на интервале (a, b).

Покажем, что пространство С[0, l] не является рефлексивным, т. е. образ ImJ отобра­жения двойственности не совпадаете С**[0, 1].

Для этого мы рассмотрим функционал (g) = g(+0) – g(0) на пространстве функций g V[0, 1] ограниченной вариации. Поскольку при всех g V[0, 1], |g(+0) – g(0)|  (g), h(+0) – h(0) = (h) = 1, где h(0) = 0 и h(x) = 1, если 0 < x  1, тo норма |||| = 1. Предположим теперь, что существует непрерывная функция f  С[0, 1] такая, что

(g) = g(+0) – g(0) = , g  V[0, 1].

В частности, равенство верно для функции g(x) = . Поэтому, подставляя эту функцию, получим

(g) = 0 =

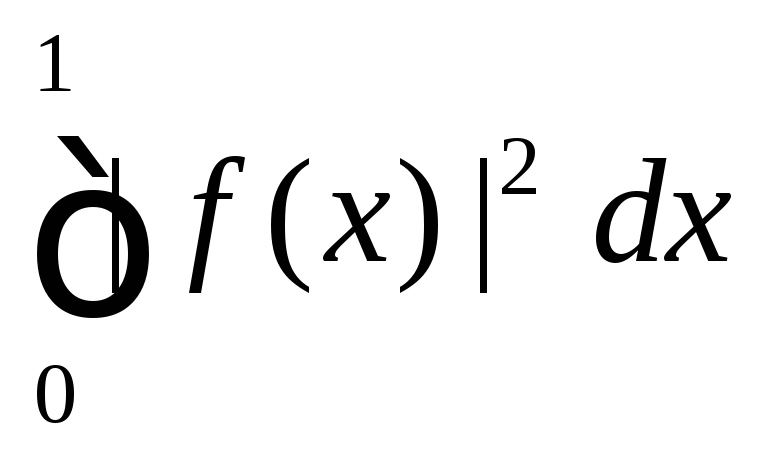
Отсюда следует, что функция равна нулю f = 0, а значит и функционал также равен нулю  = 0. Таким образом, имеет место противоречие с условием |||| = 1.