5. Примеры обратных операторов. Обратимость операторов вида (I - a) и (a - c).

Рассмотрим теперь множество линейных ограниченных операторов, отображающих линейное нормированное пространство в себя.

B пространстве операторов , действующих в ба­наховом пространствеX можно рас­сматривать произведение операторов. Именно, если , то АВ есть оператор, определяемый равенством

Отличительной особенностью этого произведения является его некоммутативность, потому что, вообще говоря, АВ ВА. Чтобы получить пример некоммутирующих операторов, достаточно взять в R_n два оператора, A и В, заданные некоммути­рующими матрицами и. Так как операторАВ за­дается произведением матриц и, что легко прове­рить, то некоммутируемость таких операторов очевидна. Свойством дистрибутивности произведение операторов обла­дает, так как из определения суммы и произведения опера­торов следует, что

т.е. что

Отметим, что если I – единичный оператор, то для любого.

Нетрудно проверить, что В самом деле, пустьиТогда

Поэтому

Из доказанного неравенства, в частности, следует, что если ив смысле равномерной сходимости, то

Прежде всего из сходимости последовательности кА следует, что есть ограниченная числовая последовательность, т. е.для любогоn. Поэтому

при так как в каждом слагаемом справа один множитель ограничен, а другой стремиться к нулю.

Частным случаем произведения операторов являются степени оператора

Ясно, что

Положим, кроме того, по определению, что

Теорема 7. Пусть гдеX – банахово пространство и Тогда операторимеет обратный линейный и ограниченный оператор, причём

Доказательство. Рассмотрим ряд

(12)

и составим частичные суммы этого ряда:

Имеем

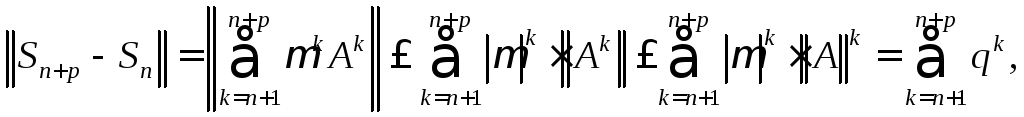
где Отсюда следует, чтоприт.е. последовательность частичных сумм ряда (12) является фундаментальной. В силу полноты пространства операторов существует

Покажем, что Имеем

ибо как общий член сходящегося ряда. Аналогично убеждаемся, чтои теорема полностью доказана.

Применим доказанную теорему к интегральным уравнениям.

Пример 19. Пусть непрерывное наядро инепрерывная нафункция. Тогда

есть линейный оператор, действующий в пространстве а интегральное уравнение

(13)

называется уравнением Фредгольма второго рода, можно записать в операторной форме

На основании предыдущей теоремы мы получаем, что если то уравнение (13) имеет единственное решение, которое даётся равенством

Рассмотрим подробнее это решение и условия, при которых оно существует. Так как то условиеочевидно, выполняется, еслиБудем считать, чтоудовлетворяет этому неравенству. Выясним, что представляют в нашем случае степени оператора. Имеем

Пусть Функцияназываетсявторой итерацией ядра

Итак,

или, меняя обозначение переменной интегрирования,

Далее,

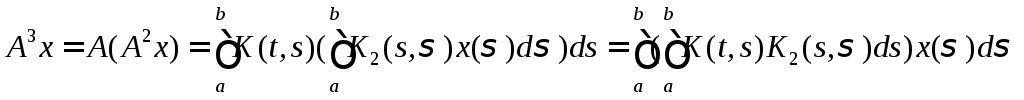
и, снова пологая

можем написать

где третья итерация ядра Вообще

где –n-я итерация ядра определяемая формулой

Равенства которое мы отмечали выше, дают

С помощью итерированных ядер решение интегрального уравнения может быть записано так:

(14)

Ряд, стоящий в правой части этого равенства, сходится в смысле сходимости в пространстве C[a, b], т.е. равномерно. Преобразуем выражение для решения интегрального уравнения. Рассмотрим формальный ряд

(15)

Этот ряд равномерно сходится на если. В самом деле, прежде всего имеем

и вообще

Отсюда гдеТаким образом, общий член исследуемого функционального ряда не превосходит по абсолютной величине члена сходящегося числового ряда, и тре­буемая равномерная сходимость доказана. Обозначим сумму этого рядаR(t, s, ). Это - непрерывная функция. Умножая члены ряда (15) наи интегрируя ряд почленно, получим

Сравнивая это выражение с выражением (14) для решения интегрального уравнения, можем написать

(16)

Это и есть выражение для обратного оператора в компактной форме. ФункцияR(t, s,)называется разре­шающим ядром рассматриваемого уравнения Фредгольма.

Сравните полученное решение с решение в главе 2 п. 2.

Пример. 20. Рассуждениями, аналогичными проведённым выше, легко показать, что если

и то интегральное уравнение (13) при значениях параметра, удовлетворяющих неравенству имеет решение, выражаемое формулой (16), где разрешающее ядроR(t, s, ), по переменным t и s имеет интегрируемый квадрат, и ряд (15), его изображающий, сходится в среднем.