2. Пространство линейных непрерывных операторов и его полнота относительно равномерной сходимости операторов

Зафиксируем два линейных нормированных пространства ии будем рассматривать всевозможные линейные непрерывные операторыА, В, … действующие из Х в Y. Определим сумму операторов и произведение операторов на число следующим образом: (А + В)х = Ах +Вх, (А)х = Ах. Это будут снова операторы, действующие из Х в Y, и легко видеть, что все необходимые свойства операций сложения и умножения на число имеют место. В частности, нулевым оператором будет оператор, определяемый равенством 0х = 0 для любого . Таким образом, совокупность всех операторов, действующих изХ в Y, есть линейное пространство. Более того, эта совокупность будет линейным нормированным пространством. В самом деле, для каждого оператора А определена норма этого оператора , являющаяся неотрицательным числом, и остаётся проверить лишь выполнение аксиом нормы.

1. Если А = 0, то для любогои потому.

Пусть, наоборот, . Тогда для любого, т. е. Ах = 0 для любого и. Первая аксиома нормы выполняется.

2. и вторая аксиома нормы тоже выполняется.

3. Подобным же образом проверяется выполнение третьей аксиомы нормы:

Итак, совокупность всех линейных непрерывных операторов, действующих из X в Y, есть линейное нормированное пространство. Это пространство мы будем обозначать символом .

В частности, когда Y = R – множество вещественных (комплексных) чисел, это пространство называется пространством линейных непрерывных функционалов, определённых на X, или сопряжённым с X пространством, и обозначается X*.

Теорема 2. Если Y – полное пространство, то – пространство линейных ограниченных операторов будет также полным пространством и, следовательно, банаховым пространством.

Доказательство. Пусть ипри,. Из обратного неравенства треугольника следует, т. е.есть сходящаяся и потому ограниченная числовая последовательность. Положим.

Возьмём любой элемент и рассмотрим последовательность. Эта последовательность фундаментальна, потому что

при ,. Так какY – полное пространство, то существует элемент , являющийся пределом этой последовательности:. Таким образом, каждомуставится в соответствие один определенный, и мы приходим к оператору, действующему изX в Y. Этот оператор линейный:

,

.

Этот оператор также ограничен:

.

Следовательно, A – линейный непрерывный оператор.

Покажем, что в смысле сходимости по норме в пространстве. Из неравенства,,, будет следовать

(7)

при ,и для любого. Пусть. Тогда (7) в пределе даетприи так как это верно для любогоx из единичного шара , то

при , что и требовалось доказать.

Следствие. Пространство X*, сопряжённое с линейным нормированным пространством X, есть банахово пространство.

Рассмотренную только что сходимость по норме в пространстве операторов называют также равномерной сходимостью последовательности операторов, потому что в этом случае сходится кравномерно на любом шаре, как это следует из неравенства

.

3. Принцип равномерной ограниченности и теорема Банаха-Штейнгауза. Полнота пространства операторов относительно поточечной сходимости

Теорема 3 (принцип равномерной ограниченности Банаха-Штейнгаузана). Если последовательность линейных ограниченных операторов L(X, Y) ограничена в каждой точке банахова пространства, то последовательность нормэтих операторов ограничена.

Доказательство. Для произвольного n рассмотрим множества

T_n = {xX: }.

В силу непрерывности операторов А_k множества T_n замкнуты: если x_iT_n и x_i  x, то n  ||A_kx_i||  ||A_kx||  n. Более того, в силу условий теоремы Х = _nT_n. Тогда, в силу теоремы Бэра хотя бы одно из T_n не является нигде не плотным множеством. Последнее означает, что существует шар пространства Х, лежащий полностью в T_n: S[y, r]  T_n. Последнее означает, что для любого k и люого х S[y, r] выполняется неравенство ||A_kx||  n. Тогда в силу леммы 3 ||A_k||  2n/r для любого k. Теорема доказана.

Следствие 1. Если для последовательности линейных ограниченных операторов L(X, Y) последовательность А_nx фундаментальна в каждой точке банахова пространства, то последовательность нормэтих операторов ограничена.

Доказательство. В силу фундаментальности последовательности А_nx в каждой точке банахова пространства, последовательность ||A_nx|| ограничена при каждом фиксированном х. Утверждение теперь легко следует из теоремы 3.

Помимо равномерной сходимости в пространстве операторов можно рассматривать ещё поточечную сходимость: сходится поточечно к, если для любого

при .

Ясно, что из равномерной сходимости следует поточечная. Обратное не верно, как показывает следующий пример.

Пример 16. В пространстве рассмотрим последовательность операторов, гдедля. Так как для любого

при , то последовательность поточечно сходится к единичному операторуI, переводящему всякий элемент из в тот же самый элемент. Однако равномерная сходимостьне имеет места, потому что для любогоn при

имеем

,

и потому для всех n

.

Следствие 2 (теорема Банаха-Штейнгаузана). Для того чтобы последовательность операторов {А_n}  L(X, Y), где Х и Y – банаховы пространства, точечно сходилась к оператору A₀, необ­ходимо и достаточно, чтобы

1) последовательность {||А_n||} была ограничена;

2) А_nх  А₀х для любого х из некоторого множества E, линейные комбинации элементов которого всюду плотны в Х.

Необходимость первого условия есть не что иное, как следствие из теоремы 3, необходи­мость второго условия очевидна. Требуется доказать лишь достаточность этих условий.

Пусть

М = ,

и пусть L(Е) – линейная оболочка множества Е. В силу линейности операторов А_n и А₀ и второго условия А_nх  А₀х для любого xL(E).

Возьмем теперь элемент y пространства X, не принад­лежащий L(E). Для заданного  > 0 найдется элемент xL(E) такой, что ||x – y|| < /4M. Имеем

||A_ny – A₀y||  ||A_ny – A_nx|| + ||A_nx – A_nx|| + ||A₀x – A₀y|| 

 ||A_nx – A_nx|| +(||A_n|| + ||A₀||)||x – y||  ||A_nx – A_nx|| + /2.

В силу того, что А_nх  А₀х, найдется номер n₀ такой, что ||A_nx – A_nx|| < /2 для n > n₀. Поэтому для n > n₀ имеем ||A_ny – A₀y|| <  и теорема доказана.

Имеет место также следующая

Теорема 4. Если пространства X и Y полные, то пространство также полно в смысле точечной сходимости.

Доказательство. Так как для каждого x последовательность фундаментальна иY полно, то для каждого x существует и мы получаем оператор, определённый наX, с областью значений в Y. Как и в теореме 1, убеждаемся, что A – линейный оператор.

Возвращаясь к оператору из неравенства,вытекающего из теоремы Банаха-Штейнгауза, в пределе приполучаем, т. е. ограниченность оператораA.

Итак, существует предел любой точечно фундаментальной последовательности линейных ограниченных операторов, который также является линейным ограниченным оператором, т. е. пространство операторов полно в смысле точечной сходимости. Теорема доказана.

Рассмотрим применение теоремы Банаха-Штейнгауза к доказательству сходимости метода механических квадратур. Для приближенного вычисления интеграла применяем формулу

,

где _n – коэффициенты формулы, x_n – узлы. Метод называется заданным, если фиксирована последовательность формул

(k – индекс).

Метод называется сходящимся, если

.

Теорема 5. Метод механических квадратур, заданный последовательностями сходится тогда и только тогда, когда

1) ;

2)  n  0 метод сходится при f(x) = xⁿ.

Необходимость практически очевидна, т. к. необходимо проверить лишь 1) условие. Но для его проверки достаточно взять кусочно-линейные непрерывные функции f_k(x), которые в узлах принимают значения (если a или b не является узлом полагаем значение функции в этой точке равной 0). Такие функции заведомо существуют и в силу сходимости и ограниченностипервое условие теоремы выполнено.

Достаточность. Рассмотрим последовательность операторов

Нетрудно видеть, что это линейные операторы из пространства C[a, b] в пространство R. В силу оценки

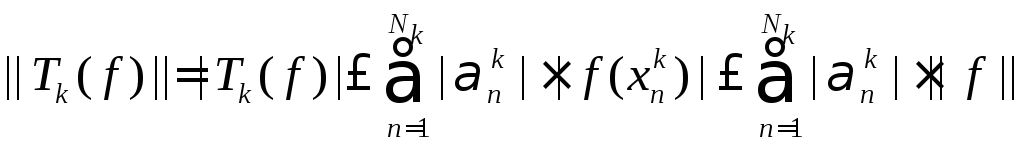
следует, что . Если взять функцииf_k(x), построенные при доказательстве необходимости, то нетрудно видеть, что ||f_k|| = 1 и . Следовательно.

Таким образом, последовательность ||T_k|| по условиям теоремы ограничена по норме и поточечно сходится на множестве {xⁿ}, линейная оболочка которого по теореме Вейерштрасса (теорема 2.7) всюду плотна в C[a, b]. По следствию 2 теоремы 3 это эквивалентно поточечной сходимости метода.