6. Заряды. Теорема Радона—Никодима

Определение 5. Пусть  — -алгебра с едини­цей X, а Ф — счетно аддитивная действительнозначная функция на М. Тогда Ф называется зарядом.

Определение 6. Пусть заряд Ф задан на -алгебре  с единицей Х и множество А . Тогда множество А называется по­ложительным (отрицательным) относительно Ф, если для лю­бого множества В , В  А выполнено неравенство Ф(В)  0 (Ф(В)  0).

Отметим, что для пустого множества в силу аддитивности заряда Ф() = 0, и пустое множество одновременно является положительным и отрицательным.

Лемма 5. Пусть Ф — заряд на -алгебре  с еди­ницей X, и пусть существует такое множество В , что Ф(В) < 0. Тогда найдется отрицательное множест­во В_о , В_о  В, Ф(В₀) < 0.

Доказательство. Если для любого A  и А  В имеем Ф(А)  0, то В само отрицательно. Пред­положим, что (В) = > 0. Сначала предположим, что(В) = +. Тогда можно выбрать измеримое множество А₁  В так, что Ф(А₁) > 1. При этом если В₁ = В\А₁, то Ф(В₁) < Ф(В) < 0. Если (В₁) < , то процесс заканчивается, а если нет, то мож­но выбрать измеримое А₂  В₁ так, что Ф(А₂) > 1, и т. д. Предположим, что процесс этот бесконечен. Тогда мы получим последовательность попарно непересекающихся измеримых множеств А₁, А₂,... с Ф(А_k) > 1 при k = 1, 2,... Но в этом случае , и мы приходим к противоречию (заряд по определению должен всюду на  принимать конечные значения). Поэтому для некоторого k по­лучим, что (В_k) < , причем Ф(B_k) < 0. В этом случае будем искать удовлетворяющее условиям леммы множество В₀ среди измеримых подмножеств множества В_k. В дальнейшем, не огра­ничивая общности, считаем, что 0 < (В) <.

Выберем измеримое множество А₁  В так, чтобы Ф(А₁) > (В)/2, и пусть В₁ = В\А₁. Тогда Ф(В₁) < Ф(В) и (В₁) < (В)/2. Если (В₁) = 0, то можно взять B₀ = B₁, в противном случае можно повторить изложенную выше операцию. В итоге либо на некотором шаге будет найдено отрицательное подмножест­во В, либо мы построим цепочку таких вложенных измеримых множеств В  В₁  В₂  ..., что Ф(В_{j + 1}) < Ф(В_j) и (B_j)  (B)/2^j при j = 1, 2,... В этом случае можно взять .

Напомним (теорема 3.4), что заряд счетно аддитивен тогда и только тогда, когда он непрерывен: Ф(В₀) = Ф(В_n). Тогда Ф(В₀) < Ф(В), а из неравенства (B_j)  (B)/2^j следует, что не существует из­меримого множества А  В₀ с Ф(А) > 0.

Теорема 19. Пусть Ф –заряд на -алгебре  с еди­ницей X. Тогда существует такое множество А₊ , что оно положительно, а множество А_ = Х\А₊ – отрица­тельно относительно заряда Ф. Представление X = А₊ + А_ называется разложением Хана заряда Ф.

Доказательство. Обозначим множество всех отри­цательных множеств A  через _ и положим . Будем считать, что  <0, иначе доказывать нечего (отрицательных множеств вообще нет). Пусть последовательность множеств из_ такова, что =. Тогда множество _ и для любого п выполнено неравенство Ф(А_)  Ф(А_n) (в силу аддитивности заряда), отку­да Ф(А_) =  (поэтому, в частности,  > –).

Докажем, что множество А₊ = Х\А_ положительно. Если это не так, то существует измеримое В  А₊ с Ф(В) < 0. Соглас­но лемме 5, можно выбрать отрицательное множество В₀  В с Ф(В₀) < 0. Но в этом случае множество С = А_ + В₀ отрица­тельно и Ф(С) <Ф(А_) = . Полученное противоречие доказы­вает теорему.

Установим единственность, в соответствующем смысле, разложения Хана.

Лемма 6. Пусть Ф – заряд на -алгебре  с единицей X и В₊ + В_ = X = А₊ + А_ – два разложения Хана. Тогда для любого Е  имеем Ф(ЕА₊) = Ф(ЕВ₊) и Ф(ЕА_) = Ф(ЕВ_).

Доказательство. Поскольку множество Е(А₊\В₊) одновременно является подмножеством и А₊ и В_, Ф(Е(А₊ \ В₊)) = 0. Аналогично, Ф(Е(В₊ \ А₊)) = 0. Поэтому Ф(ЕА₊) = Ф(Е(А₊ В₊)) = Ф(ЕВ₊). Аналогично устанавливается второе равенство.

Определение 7. Если Ф — заряд на -алгебре  с единицей X и X = А₊+А_ –разложение Хана, то можно однозначно определить две -аддитивные меры Ф⁺(Е) = Ф(ЕА₊) и Ф^–(Е) = –Ф(ЕА_). Разложение Ф = Ф⁺ – Ф^– называется разложением Жордана заряда Ф, а мера Ф = Ф⁺ + Ф^– – полной вариацией исходного заряда.

Определение 8. Пусть (X, , ) — -конечное из­меримое пространство, а Ф – заряд на . Тогда Ф называется абсолютно непрерывным относительно меры , если из того что Е  и (Е) = 0, вытекает, что Ф(Е) = 0.

Лемма 7. Пусть (X, , ) – конечное измеримое пространство, а Ф – -аддитивная мера на , абсолют­но непрерывная относительно меры , и Ф не равен тождественно нулю. Тогда су­ществуют такое натуральное число n и такое множест­во В , что (В) > 0 и В положительно относительно заряда _n = Ф .

Доказательство. Пусть X = A₊(i) + A_(i) – разло­жение Хана относительно заряда _i, где i = 1, 2,... При этом можно считать, что А₊(1)  А₊(2)  ... Далее, пусть и . Очевидно, что X = А₊ А_. Тогда для любого m имеем _m(А_) <0, т. е. Ф(А_)  ,откуда Ф(А_) = 0. Поэтому Ф(А₊) > 0, а следовательно, и (А₊) > 0. Согласно свойству непрерывности меры найдется такое n, что (А₊(n)) > 0. Но по определе­нию множество А₊(n) положительно относительно заряда _n, что и завершает доказательство.

Теорема 20 (Радона—Никодима). Пусть (X, , ) — -конечное из­меримое пространство, а Ф — за­ряд на , абсолютно непрерывный относительно меры . Тогда существует такая интегрируема по Лебегу функция f(x), что для любого А  справедливо равенство

.

При этом если для некоторой другой интегрируемой функции g(x) равенство также выполняется для всех А , то f(x) = g(x) почти всюду относительно меры .

Доказательство. Благодаря наличию разложения Жордана, достаточно доказать теорему для случая, когда Ф – мера. Сначала рассмотрим случай (Х) < . Определим множество

.

Пусть также . Тогда найдется такая последовательность {f_n(x)} F, что . Определим приn = 1, 2, … и хХ функцию g_n(x) = . Тогда по следствию 2 леммы 4.1 g_n(x) измерима на X, а поскольку , то и интегрируема при всех п. Проверим, что g_n(x) F. Неотри­цательность этой функции очевидна. Далее, в силу определения функции g_n(x) ее можно представить в виде

, где X = .

Отсюда для любого А  имеем

,

т. е. действительно g_n(x) F. Заметим, что функции {g_n(x)} образуют неубывающую наX последовательность. Определим функцию f(x) = .Поскольку при п = 1, 2,...  S, то по теореме 13 о монотонной сходимости функция f(x) интегрируема и конечна почти всюду на X. Так как , то и функция f(x) F. Кроме того,

,

откуда .

Теперь рассмотрим заряд (А) = Ф(А) – для любогоА . Этот заряд, очевидно, неотрицателен (т. е. является -аддитивной мерой) и абсолютно непрерывен относительно меры . Предположим, что заряд  не равен тождественно нулю. Тогда по лем­ме 7 найдутся такое n и такое множество В , что (В) > 0 и для любого измеримого А  В имеем , т. е.. Определим функцию h(x) = при x X. Тогда для любого А имеем

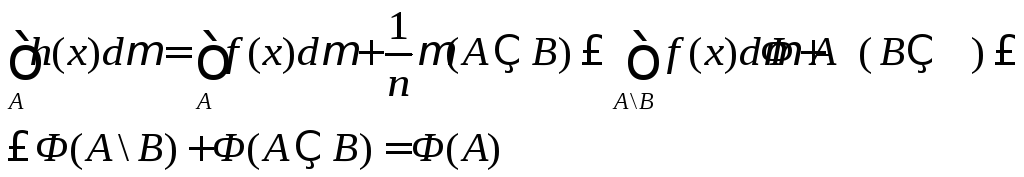
Поэтому h(x) F, в то время, как

Полученное противоречие показывает, что  = 0 на , и для случая конечного измеримого пространства доказатель­ство существования завершено.

Пусть теперь X = ,где (E_n) <  при n = 1, 2, … Согласно уже рассмотренному случаю, для каждого n найдется такая интегрируемая на E_n функция f_n(x), что для любого множества А  E_n = _n

. (4)

Заметим, что все функции f_n(x) неотрицательны на области сво­его определения. Продолжим их нулем на все множество X и по­ложим . Тогда

,

откуда следует интегрируемость на Х функции f(x). Нужное нам равенство сразу выте­кает из равенств (4) и счетной аддитивности заряда..

Проверим единственность с точностью до почти всюду по­строенной функции. Если для любого А 

,

то, обозначая X₁ = {xX: f(x) > g(x)} и Х₂ = {х  X: f(x) < g(х)}, получим, что

.

Последнее равенство возможно, только если (Х₁) = 0. Анало­гично, (Х₂) = 0, и теорема Радона—Никодима полностью до­казана.

7. -аддитивность прямого произведения мер. Теорема Фубини

Обозначим через X = Х₁Х₂ прямое произведение пространств X₁ и Х₂. Каждая точка х = (x₁, х₂) этого пространства X является упорядоченной парой некоторых точек х_i пространств X_i, i = 1, 2.

Если в пространстве X_i (i = 1, 2) задано полукольцо множеств _i, то через  = ₁₂ будем обозначать произведение полуколец. По лемме 3.1 эта система множеств является полукольцом в пространстве X.

Предположим, что заданы меры m_i на полукольцах _i множеств пространств X_i, i = 1, 2. Тогда функция множества m = m₁m₂ определенная на системе  множеств пространства X по формуле

m(А) = m₁(А₁)m₂(А₂), A = A₁А₂

называется прямым произведением мер m_i.

Теорема 21. Пусть m_i – счетно-аддитивные меры, заданные на полукольцах _i, i = 1, 2.

Тогда функция множества m = m₁m₂ опреде­ленная на системе  = ₁₂ является счетно-аддитивной мерой.

Доказательство. Рассмотрим счетную сумму множеств

A, A_i  ₁, B, B_i  ₂.

Рассмотрим полукольцо ₁А с единицей А. Тогда m₁ является счетно-аддитивной мерой на ₁А. В соответствии с теоремой 3.10 мы можем построить продолжение этой меры на -алгебру измеримых множеств ₁. Обозначим это продолжение через ₁. Определим функции h_i(x₁) = m₂(B_i)(x₁), i = 1, 2, … Эта функция является простой на А. Для каждого х₁ А положим J(x₁) = {i: x₁  A_i} (заметим, что дизъюнктность множеств A_iB_i вообще говоря не влечет дизъюнктность множеств A_i). Так как для любого у В пара (х₁, у) АВ, то выполняется равенство В = . В силу счетной аддитивности мерыm₂

.

Кроме того,

< .

Так как все функции, входящие в сумму неотрицательные и, следовательно, частичные суммы монотонно возрастают, можно в последнем равенстве поменять местами интеграл и сумму (теорема о монотонной сходимости)

.

Следовательно, функция множества m = m₁m₂ на  является счетно-аддитивной мерой.

Определение 9. Мера  в пространстве X, которая получается в результате стандартного продолжения пря­мого произведения мер m = m₁m₂ с полукольца  = ₁₂ на -алгебру  измеримых множеств с единицей X называется произведением мер.

Далее мы считаем, что меры ₁ и ₂ заданы на -алгебрах ₁ и ₂ и произведение этих мер  = ₁₂ задано на -алгебре  и является продолжением с ₁₂.

Прежде чем мы сможем в полном объеме доказать теоре­му Фубини, установим некоторые ее частные случаи. Предва­рительно введем такое обозначение. Если множество Е  X = Х₁Х₂, то при любом х  Х₁ обозначим через Е(х)  Х₂ соответствующее сечение, т. е. Е(х) = {уХ₂: (х, у)Е}.

Аналогично, при любом у Х₂ определяется сечение Е(у) Х₁.

Теорема 22. Пусть меры ₁ и ₂ -конечны и пол­ны,  = ₁₂, множество Е  и (Е)<. Тогда для почти всех, относительно меры ₁, точек хХ₁ сечение E(x)₂, функция ₂(E(х)) интегрируема на Х₁ и

. (5)

Здесь мы произвольным образом доопределяем функцию ₂(E(х)) в тех точках, где она не существует. Разумеется, аналогичное представление остается справедливым, если мы поменяем ролями ₁ и ₂.

Доказательство. Ясно, что утверждение теоремы справедливо для множеств Е ₁₂, а тогда, в силу линейности обеих частей формулы (5), и для любого Е, представимого в виде конечного дизъюнктного объединения множеств из полукольца ₁₂ (см. задачу 3.13).

Пусть теперь Е произвольное измеримое множество конечной меры. Рассмотрим его измеримую оболочку А (теорема 3.12). Тогда по построению измеримой оболочки Е = А\Н, где множество Н имеет меру нуль: (Н) = 0 и

, где В_ij .

Пусть и. Тогда имеет место равенствои

,

причем множества D_nk имеют вид и обязаны принад­лежать минимальному кольцу, содержащему. Заметим, что эта последовательность множеств не убывает D_n1  D_n2  …и  ₂(D_nk(x))   ₂(C_n(x)). Поэтому по теореме о монотонной сходимости интеграла утверждение леммы верно для множеств С_n. Аналогично, последовательность множеств С₁  С₂  … не возрастает и ₂(C_n(x))  ₂(A(x)). Значит утверждение верно для множества A.

Осталось проверить утверждение для множеств Н  Х₁X₂ меры нуль, (H) = 0. Пусть F есть измери­мая оболочка множества H, тогда (H) = (F) = 0, и по доказанному выше, мы имеем равенство

(H) = (F) = = 0

Из свойств интеграла Лебега вытекает, что п. в. сечения вида F(х) имеют меру нуль, ₂(F(х)) = 0. Так как H(х)  F(х), то тем более ₂(Н(х)) = 0 при п в. х X. Следователь­но, функция f(x) = ₂(Н(х)) эквивалентна нулю и утверждение доказано.

В доказанной теореме переменные х и у можно поменять места­ми. Поэтому п. в. сечения Е(х) ₂ и Е(у) ₁ измеримого множества Е конечной меры будут измеримы, функции f(x) = ₂(Е(х)) и g(y) = ₁(E(у)) эквивалентны измеримым функциям, при этом имеют место равенства

.

Применяя счетную аддитивность интеграла и теорему о монотонной сходимости, нетрудно доказать теорему и для множеств Е  -конечной меры. Таким образом, п. в. сечения Е(х) и Е(у) множества -конечной меры измеримы, a f(x) = ₂(Е(х)) и g(y) = ₁(E(у)) эквивалентны измеримым функциям. Если Е не имеет -конечной меры, то утвер­ждение леммы может быть неверным.

Пусть для множества Е  X = Х₁Х₂ функция f действует из Е в R. Тогда функция f_х(у) = f (х, у), определенная на множестве Е(х), называется сечением функции f по переменной х. Если Е(х) пусто, то по определению полагаем f_х(у) = 0.

Теорема 23 (Фубини). Если функция f интегрируема на множестве Е  -конечной меры, то при почти всех хХ сечения f_x измеримы на множестве Е(х), при почти всех yХ₂ сечения f_y измеримы на множестве Е(у), а их интегралы

,

эквивалентны измеримым функциям. При этом

.

Доказательство. Мы докажем теорему для сечений по переменной х. Вначале предположим, что для простых функций теорема уже доказана. По определению инте­грала Лебега каждая интегрируемая функция является разностью f = f₊ – (–f_) неотрицательных интегрируемых функций. Поэтому нам достаточно рассмотреть неотри­цательные интегрируемые функции f  0.

В этом случае существует монотонная последователь­ность простых неотрицательных интегрируемых функций f_n  f, сходящаяся к функции f на множестве Е. Так как сечения этих функций f_nxf_x сходятся монотонно на множестве Е(x), то по теореме о монотонной сходимости при п. в. x Х₁ имеет место равенство

.

Заметим, что по предположению интегралы от простых функций f_nx не убывают и эквивалентны измеримым функциям. Поэтому можно еще раз применить теорему о монотонной сходимости. Таким образом, интеграл будет также эквивалентен измеримой функции и

.

Докажем теорему для простых интегрируемых функций. В силу свойства линейности интеграла нам достаточно рассмотреть только характеристические функции f = _E измеримых множеств Е конечной меры (Е) < . В этом случае теорема Фубини принимает вид

.

При этом утверждается, что сечения Е_х ₂ измеримы при п. в. х Х₁ и функция g(x) = ₂(Е(x)) эквивалентна измеримой функции. Таким образом, мы свели теорему к уже доказанной теореме 22.

Следует отметить, что в общем слу­чае даже существование обоих повторных интегралов и их ра­венство не влечет существования двойного интеграла.

Задачи

1. Интегрируема ли по Риману на отрезке [0, 1] функция f (x), которая равна х³ если х иррационально, и равна 1, если х рационально. Интегрируема ли она по Лебегу на отрезке [0, 1]? Если да, то чему равны эти интегралы?

2. Пусть f (x) – неотрицательная интегрируемая функция на Е и E{ f (x)  c} = a. Доказать, что .

3. Пусть f (x) – интегрируемая на [a, b] функция. Доказать, что если при любомc [a, b], то f (x) = 0 почти всюду на [a, b].

4. Интегрируемы ли по Лебегу функции 1/х и 1/х² на интервале (0, 1)?

5. Пусть ограниченная функция f (x) интегрируема по Лебегу на множестве Е. Будут ли интегрируемы по Лебегу на этом множестве функции (f (x))¹⁰, | f (x)|, 1/ f (x), cos f (x)?

6. Пусть функция f (x) неотрицательна и измерима на множестве Е конечной меры. Доказать, что эта функция интегрируема на Е тогда и только тогда, когда сходится ряд , гдеЕ_k = E{k  f (x)  k + 1}.

7. Доказать, что если функция f (x) интегрируема на отрезке [0, a], то при любом k > 0 функция f (kx) интегрируема на отрезке [0, a/k] и

.

8. Пусть функция f (x) измерима на множестве Е конечной меры. Доказать, что существует положительная измеримая на Е функция (х) такая, что произведение f (x) (х) интегрируемо на Е.

9. Привести пример функции f (x), которая непрерывна на промежутке (a, b], имеет сходящийся несобственный интеграл Римана (R), но не является интегрируемой по Лебегу на (a, b).

10. Пусть - последовательность измеримых наЕ ограниченных неотрицательных функций. Пусть  0 при n  . Следует ли из этого, что f_n(x)  0 при n   всюду или хотя бы почти всюду на Е?

11. Построить на каком-либо множестве Е конечной меры последовательность ограниченных измеримых функций , сходящуюся почти всюду наЕ к функции , которая не интегрируема на Е.

12. Доказать, что измеримая на множестве Е конечной меры неотрицательная функция f (x) и нтегрируема по Лебегу тогда и только тогда, когда сходится ряд , гдеE_k = E{ f (x)  k}

13. Пусть функция f (x) непрерывна на промежутке (a, b]. Доказать, что если функция f (x) интегрируема по Лебегу на отрезке [a, b], то существует несобственный интеграл в обычном смысле на этом отрезке и его значение совпадает со значением интеграла Лебега.

14. Доказать, что существует функция f (x) непрерывна на промежутке (a, b], для которой несобственный интеграл на отрезке [a, b] сходится, а интеграл Лебега на этом отрезке не существует.

15. Пусть f (x) – измеримая функция, определенная на множестве Е конечной меры. Определим срезки функции

.

Назовем Q-интегралом функции f (x) следующий предел (если он существует)

.

Доказать, что функция f (x) интегрируемая по Лебегу на Е также Q-интегрируема и интегралы равны.

16. Привести пример не интегрируемой по Лебегу функции, у которой Q-интеграл существует.

17. Доказать, что для неотрицательной измеримой функции f (x) из существования Q-интеграла вытекает интегрируемость по Лебегу функции f (x).

18. Доказать, что любая измеримая нечетная на отрезке [-a, a] функция f (x) Q-интегрируема на этом отрезке.

19. Справедливо ли утверждение: если измеримая функция f (x) Q-интегрируема на множестве Е, то она Q-интегрируема на любом его измеримом подмножестве?

20. Справедливо ли утверждение: если измеримая функция f (x) Q-интегрируема на множестве Е, то функция с f (x) также Q-интегрируема на множестве Е и справедливо равенство

?

21. Справедливо ли утверждение: если измеримые функции f (x) и g(x) Q-интегрируемы на множестве Е, то функция f (x) + g(x) также Q-интегрируема и справедливо равенство

.

22. Справедливо ли утверждение: если измеримые функции f (x), g(x) и f (x) + g(x) Q-интегрируемы на множестве Е, то справедливо равенство

.

23. Пусть на отрезке [а, b] задана конечная вещественная функция f (x). Разобъем отрезок [а, b] на части точками x₀ = a < x₁ < …< x_n = b и составим сумму

.

Точная верхняя грань всевозможных сумм V называется полной вариацией функции f (x) на отрезке [а, b] и обозначается . Если полная вариацииf (x) конечна, то функция называется функцией ограниченной вариации. Доказать, что любую функцию ограниченной вариации можно разложить на разность двух невозрастающих функций.

24. Показать, что функция ограниченной вариации f (x), непрерывная слева, определяет равенством v([с, d)) = f (d) - f (c) заряд на полукольце ₁[а, b] (см. глава 3).