5. Сравнение интегралов Римана и Лебега

Пусть на отрезке [а, b] задана (не обязательно конечная) функ­ция f(х). Пусть x₀  [a, b] и  > 0. Обозначим через m_(x₀) и М_(х₀) соответственно точную нижнюю и точную верхнюю границы функ­ции f(x) на интервале (х₀ - , x₀ + ):

m_(x₀) = inf{f(x)}, M_(x₀) = sup{f(x)} (х₀ -   x  x₀ + ).

(Само собою разумеется, что мы принимаем во внимание лишь те точки интервала (х₀ - , x₀ + ), которые лежат также и на отрезке [а, b].) Очевидно, m_(x₀)  f(x₀)  M_(x₀).

Если  уменьшается, то m_(x₀) не убывает, a M_(x₀) не возра­стает. Поэтому существуют пределы (конечные или бесконечные)

m(x₀) = m_(x₀), M_(x₀) = M_(x₀),

причем, очевидно, m_(x₀)  m(x₀)  f(x₀)  M(x₀)  M_(x₀).

Определение 4. Функции т(х) и М(х) называются соответственно нижней и верхней функциями Бэра для функции f(x).

Теорема 15 (Бэр). Пусть функция f(х) конечна в точке х₀. Для того чтобы f(x) была в этой точке непрерывна, необходимо и достаточно, чтобы было m(x₀) = M(x₀).

Доказательство. Допустим, что функция f(х) непрерывна в точке x₀. Взяв произвольное  > 0, найдем такое  > 0, что как только  , так сейчас же  . Иначе говоря, для всех х  (х₀ - , x₀ + ) будет f(x₀) -   f(x)  f(x₀) + . Но отсюда следует, что f(x₀) -   m_(x₀)  M_(x₀)  f(x₀) + , а стало быть, и тем более f(x₀) -   m(x₀)  M(x₀)  f(x₀) + , откуда, ввиду произвольности , и вытекает доказываемое равенство. Итак, необходимость доказана.

Пусть теперь выполнено равенство m(x₀) = M(x₀). Тогда, оче­видно, m(x₀) = M(x₀) = f(x₀) и общее значение функций Бэра в точке x₀ конечно.

Возьмем произвольное  > 0 и найдем столь малое  > 0, что

m(x₀) -   m_(x₀)  m(x₀), M(x₀)  M_(x₀)  M(x₀) + .

Такое  найдется в силу определения функций Бэра. Эти неравенства означают, что

f(x₀) -   m_(x₀), M_(x₀)  f(x₀) + .

Если теперь x  (х₀ - , x₀ + ), то f(x) лежит между m_(x₀) и M_(x₀), так что f(x₀) -   f(x)  f(x₀) + . Иначе говоря, из того, что   вытекает, что  , т. е. функция f(x) непрерывна в точке х₀.

Теорема 16. Функции Бэра т(х) и М(х) измеримы.

Доказательство. Проведем доказательство для нижней функции Бэра, для верхней это делается аналогично.

Пусть х₀  [a, b]{m(x) > c}. Тогда для некоторого  > 0 выполняется неравенство m(x₀) > c + . По определению нижней функции Бэра и свойствам предела найдется такое  > 0, что m_(x₀) > c + , т.е. для любого x [a, b](x₀ - , x₀ + ) выполняется неравенство f(x) > c + . Пусть x₁ [a, b](x₀ - , x₀ + ). Тогда найдется ₁ > 0 такое, что (x₁ - ₁, x₁ + ₁)  (x₀ - , x₀ + ) и, следовательно, . В силу определения нижней функции m(x₁)  с +  > c. Этим показано, что [a, b](x₀ - , x₀ + )  [a, b]{m(x) > c} и множество [a, b]{m(x) > c} является открытым в [a, b], а значит и измеримым. Этим показано, что одно из множеств Лебега нижней функции Бэра измеримо и, следовательно, сама функция измерима.

Теорема 17 (Лебег). Для того чтобы ограниченная функ­ция f(x) была интегрируема (R) на отрезке [a, b], необходимо и достаточно, чтобы она была непрерывна почти везде.

Доказательство. По определению нижнего интеграла Дарбу и результатов математического анализа известно, что существует такая последовательность разбиений _k = отрезка [a, b], что нижний интеграл Дарбу равен

,

где . В силу свойств монотонности сумм Дарбу, можно считать, что каждое следующее разбиение_{k + 1} является размельчением для предыдущего _k и диаметры разбиений стремятся к нулю ( 0 при k ).

Определим последовательность простых функций

.

Ясно, что эта последовательность функций не убывает, и если х не является граничной точкой для всех промежутков _ik разбиений _k, то . Так как концов отрезков_ik счетное число, то оно имеет меру нуль, и последовательность h_k(x)m(x) п.в. Так как интеграл Лебега от простой функции h_k(x) равен (лемма 3), по теореме о монотонной сходимости получаем

.

Аналогично устанавливается равенство для верхнего интеграла Дарбу

,

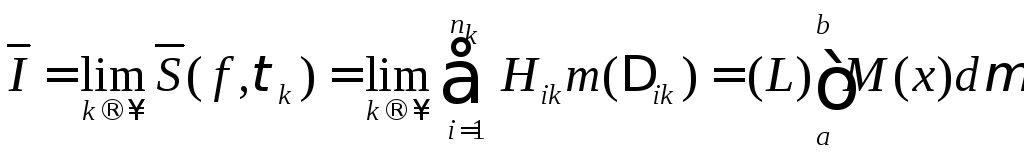где .

В соответствии с общей теорией интеграла Римана для интегрируемости функции f(x) на отрезке [a, b] необходимо и достаточно, чтобы верхний и нижний интегралы Дарбу совпадали. Следовательно,

или

Так как подинтегральная функция неотрицательна, то согласно теоремы 12, подинтегральная функция обязана быть равной 0 почти всюду, что по теореме 15 означает непрерывность функции f(x) почти всюду.

Эта замечательная теорема представляет собой наиболее простой и ясный признак интегрируемости (R). В частности, она оправды­вает сделанное ранее замечание, что интегрируемыми (R) могут быть только «не очень разрывные» функции.

Допустим теперь, что функция f(x) интегрируема (R). Тогда она необходимо ограничена и почти везде будет т(х) = М(х). Но ведь т(х)  f(x)  М(х). Значит, почти везде f(x) = m(x), и f(x), будучи эквивалентна измеримой функции т(х), измерима сама. Так как всякая ограниченная измеримая функция интегри­руема (L), то такова же и f(x), т. е. из интегрируемости какой-нибудь функции в смысле Римана вытекает ее интегрируемость в смысле Лебега.

Наконец, из эквивалентности функций f(x) и т(х) следует, что

(L) = (L) .

Но, как известно из курса математического анализа, в условиях основной леммы для интегрируемой (R) функции f(x) будет s_i  (R), где s_i есть нижняя сумма Дарбу, отвечающая i-му способу дробле­ния. Как показано выше s_i  (L) , а, следовательно

(R) = (L) .

Таким образом, справедлива теорема.

Теорема 18. Всякая функция, интегрируемая (R), необходимо интегрируема и (L), и оба ее интеграла равны между собой.

В заключение отметим, что функция Дирихле (x) (равная нулю в иррациональных и единице в рациональных точках) интегри­руема (L) (ибо она эквивалентна нулю), но, как мы видели в пункте 2, не интегрируема (R), так что теорема 17 не обратима.