7. Мера Лебега на Rn

Пусть m мера, простроенная по теореме 7 на полукольце ячеек. Эта мера порождает внешнюю меру (теорема 8). Мера, порожденная этой внешней мерой на множествах из R_n называется мерой Лебега на R_n.

Следующая теорема является аналогом ранее доказанной теоремы о структуре открытых множеств на числовой прямой.

Теорема 13. Всякое открытое множество G  R_n представимо в виде не более чем счет­ного объединения дизъюнктных n-мерных открытых параллелепипедов с конечными ребрами.

Теорема 14. Каждое открытое и каждое замкнутое множество из R_n измеримо.

Доказательство. Легко вытекает из того, что все ячейки в R_n измеримы по теореме 9, далее система измеримых множеств -алгебра (теорема 9) и любой открытый параллелепипед можно представить в виде счетного объединения возрастающей последовательности ячеек. Воспользовавшись теперь теоремой 13 и снова замкнутостью системы измеримых множеств относительно счетного объединения, получим измеримость любого открытого множества. Измеримость замкнутых множеств получается опять же в силу замкнутости системы измеримых множеств относительно операции дополнения.

Теорема 15. Любой параллелепипед  измерим, при этом () = V_.

Доказательство. Доказательство легко вытекает из вложений ₀Е  Е  *Е и вытекающего отсюда неравенства внешних мер *(₀Е)  *(Е)  *(*Е), а также равенства *(*\₀) = 0.

Теорема 16. Всякое конечное или счетное множество А точек из R_n измеримо и его мера равна 0.

Доказательство. Пронумеруем точки множества А в виде последовательности z_n. Возьмем произвольное  > 0. Поместим каждую точку в n-мерный куб (открытый или замкнутый), объем которого не превосходит /2ⁿ. Тогда *(А)  . В силу теоремы 11 это означает, что множество А измеримо и имеет меру 0.

Определение 28. Борелевскими множествами называют множества, принадлежащие наименьшей -алгебре множеств, содержащей все открытые и замкнутые множества в R_n.

Так как по теореме 14 все открытые и замкнутые множества измеримы, а все измеримые множества образуют -алгебру, то очевидна следующая теорема.

Теорема 17. Все борелевские множества из R_n измеримы.

Теорема 18. Внешняя мера любого множества Е  R_n равна нижней грани мер всевоз­можных открытых множеств, содержащих Е

*(Е) = μ(G)

Доказательство. Утверждение практически очевидно, так как, покрывая множество ячейками, мы легко можем покрыть это множество открытыми параллелепипедами, объем которых в совокупности отличается от объема покрытия ячейками на сколь угодно малое положительное число.

Теорема 19. Мера любого ограниченного измеримого множества Е  R_n равна верхней грани мер всевоз­можных замкнутых множеств, содержащихся в Е

(Е) = μ(F)

Доказательство. Поместим множество Е в некий замкнутый ограниченный параллелепипед Р. При этом предполагаем, что внутренность параллелепипеда Р также содержит множество Е. В силу ограниченности множества Е это можно сделать. В силу свойств меры множество Р – Е измеримо. Из теоремы 18 и свойств меры вытекает (в силу условий на Р наименьшую грань можно брать только по открытым множествам содержащимся в Р):

(Е) = (Р – (Р – Е)) = (Р) - (Р – Е) = (Р) - μ(G) = (Р – G).

В силу открытости множества G множество F = P – G является замкнутым. Отсюда вытекает утверждение теоремы.

Задачи

1. Доказать, что система всех конечных подмножеств заданного множестваявляется кольцом.

2. Найти в задаче 1. условие на множество , необходимое и достаточное для того, чтобы кольцоявлялось алгеброй.

3. Пусть – бесконечное множество, а– система всех не более чем счетных подмножеств. Доказать, чтоявляется-кольцом.

4. Найти в задаче 3. условие на , необходимое и достаточное для того, чтобыявлялось-алгеброй.

5. Пусть – множество,– система всех таких множеств, что либо, либоне более чем счетно. Доказать, чтоявляется-алгеброй.

6. Пусть – множество,– система всех таких множеств, что либо, либоконечно. Доказать чтоявляется алгеброй.

7. Доказать, что система всех интервалов, отрезков и полуинтервалов из отрезка образует полукольцо.

8. Доказать, что система всех интервалов (включая пустой) и система всех отрезков (с добавлением пустого множества) в R не является полукольцом.

9. Доказать, что система всех открытых множеств в R не является полукольцом.

10. Пусть – полукольцо (кольцо),. Доказать, что система– полукольцо (алгебра) (эту систему мы будем обозначать через).

11. Построить систему множеств, которая замкнута относительно операций и, но не является даже полукольцом.

12. Пусть – полукольцо. Доказать, что системаявляется кольцом.

13. Пусть – полукольцо. Доказать, что система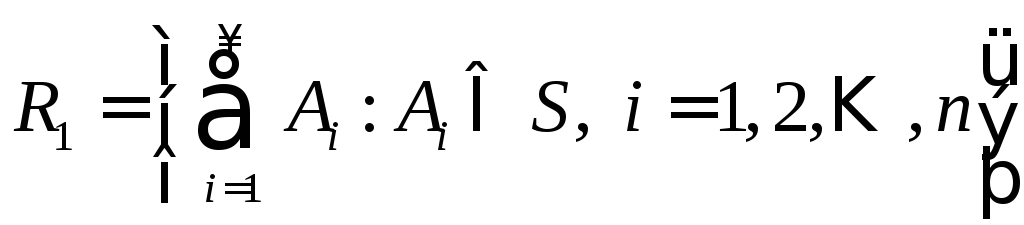совпадает с кольцом, определенным в задаче 12.

14. Доказать, что пересечение произвольной непустой системы колец является кольцом (возможно, кольцом ).

15. Доказать, что пересечение произвольной непустой системы -колец является-кольцом.

16. Доказать, что пересечение произвольной системы алгебр с одной и той же единицей является алгеброй.

17. Привести пример двух -алгебр, пересечение которых не является алгеброй.

18. Доказать, что не существует кольца, содержащего ровно 3 различных множества (включая пустое).

19. Построить пример -алгебритаких, чтоне является кольцом.

20. Доказать, что произведение -алгебрис единицамииявляется кольцом тогда и только тогда, когда хотя бы одна из этих-алгебр содержит не более двух множеств.

21. Пусть даны множества и, функция, а– система множеств в. Положимдляи. Доказать, что если– полукольцо, то– полукольцо.

22. В условиях задачи 21 доказать, что если – кольцо, то– тоже кольцо.

23. В условиях задачи 21 доказать, что если –-алгебра, то– тоже-алгебра.

24. Построить множества ,, функциюи кольцоподмножествтакие, чтоне является полукольцом.

25. Пусть задано полукольцо ₁ промежутков [a, b) (см. теорема 3) и неубывающая ограниченная функция g(x) на числовой прямой. Определим функцию множеств m([a, b)) = g(b) – g(a). Доказать, что m является счетно-аддитивной мерой на ₁ тогда и только тогда, когда функция g(x) непрерывна слева во всех точках. (Замечание. Мера, которая получается из этой меры при продолжении называется мерой Лебега-Стильтьеса).