7. Отображение компактных множеств. Теорема Вейерштраса об ограниченности и достижении точных граней непрерывной функцией

Теорема 9. Пусть Х, У – топологические пространства, Х компактно, а f: Х  У – непрерывное отображение. Тогда образ f(Х) – компактное пространство в У.

Доказательство. Пусть {V_} - произвольное открытое покрытие f (Х). В силу определения непрерывного отображения, множества f ^-1(V_) также являются открытыми и, очевидно, образуют открытое покрытие для Х. В силу компактности Х существует конечный набор из этого покрытия такой, что . Но в этом случае иf (Х) , что доказывает компактностьf (Х).

Теорема 10. Пусть Х, У – топологические пространства, Х компактно, У – отделимое, а f: Х  У – непрерывное отображение. Тогда f замкнутое отображение.

Доказательство. Всякое замкнутое множество компактного пространства само является компактным множеством (теорема 1.13). Итак, пусть В – замкнутое множество в пространстве Х (следовательно компактное). По предыдущей теореме f (В) – компактное множество. В силу отделимости У это множество обязано быть замкнутым (теорема 1.15).

Теорема 11. Пусть Х, У – топологические пространства, Х компактно, У – отделимое, а f: Х  У – непрерывное биективное отображение. Тогда f - гомеоморфизм.

Доказательство практически очевидное.

Теорема 12 (Вейерштрасса). Всякая непрерывная функция f : Х  R на компактном пространстве Х ограничена и достигает на Х своей верхней (нижней) грани.

Доказательство. В силу компактности Х и непрерывности f образ f (X) является компактным множеством в R. Но любое компактное множество в R ограничено и замкнуто. Ограниченность f (X) означает ограниченность функции. Замкнутость числового множества f (X) влечет принадлежность ему его точных граней. Это означает, что точная грань (например, супремум) достигается на каком-то элементе х₀ Х, т.е. f (x₀) = sup f (X).

Теорема 13 (Кантора). Всякая непрерывная функция f(x), определённая на компактном множестве Q, метрического пространства (Х, ), равномерно непрерывна на нём: иными словами, для любого ε > 0 можно найти такое δ>0, что из ρ(x, y)< δ следует |f(x) - f(y)| < ε

Доказательство. Допуская противное, мы для некоторого ε₀ сможем указать такие последовательности x_n и y_n, что

ρ (x_n, y_n)< , |f(x_n) - f(y_n)| ε₀ (12)

Последовательность {x_n} в силу предположения содержит подпоследовательность {x_ni}, сходящуюся к некоторой точке х₀. Тогда и подпоследовательность {y_ni} сходится к точке х₀. Начиная с некоторого номера, точки x_ni и y_ni попадают в такую окрестность точки х₀ , в которой выполняется неравенство |f(x ) - f(x₀)|<. Но тогда

|f(x_ni ) - f(y_ni)| |f(x_ni) - f(х₀)| + |f(x₀) - f(y_ni)| < += ε₀

что противоречит условию (12). Теорема доказана.

8. Принцип сжимающих отображений и его применение

Определение 14. Отображение А метрического пространства X в себя называется сжимающим, если d(Ax, Ay)  d(x, y), где 0<<1.

Теорема 14 (Принцип сжимающих отображений). Если А: XX сжимающее отображение в полном метрическом пространстве (X, d), то  единственная точка уХ: Ay = y (неподвижная точка).

Доказательство. Для произвольного x₁X определим x₂ = Ax₁, x₃ = Ax₂, ... x_k = Ax_k-1. Получим последовательность {x_k}, для которой d(x₃, x₂) = d(Ax₂, Ax₁)  d(x₂, x₁). По такой же схеме выводим общую формулу: d(xⁿ⁺¹ , xⁿ) = d(Ax_n, Ax_n-1)  d(x_n, x_n-1)  ...  ^n-1 d(x₂, x₁). По неравенству треугольника и выведенной формуле получаем

d(x_n+p, x_n)  d(x_n+p, x_n+p-1) +...+ d(x_n+1, x_n)  (^n+p-2 + ^n+p-3 +...+ ^n-1) d(x₂, x₁) = ^n-1(1 – ^p)d(x₂, x₁)/(1 – )  ^n-1d(x₂, x₁)/(1 – )

(внутреннее равенство – сумма геометрической прогрессии).

В силу неравенства 0<<1 и неравенства d(x_n+p, x_n)  ^n-1d(x₂, x₁)/(1 - ) для >0  N: d(x_n+p, x_n) < , n  N и любого натурального р. Таким образом, последовательность {x_n} является фундаментальной, а следовательно в силу полноты пространства x_n  x₀ Х

Теперь докажем, что Аx₀ = x₀. Имеем d(Ax₀, x₀)  d(Ax₀, x_n) + d(x_n, x₀) < d(Ax₀, Ax_n-1) +   d(x₀, x_n-1) +  < 2 (<1) при достаточно больших n. В силу произвольности >0 из этого неравенства вытекает, что d(Ax₀, x₀) = 0. Из аксиом метрики вытекает нужное нам равенство.

Докажем единственность неподвижной точки. Пусть y₀X: Ay₀ = y₀ и y₀  x₀. Тогда d(x₀, y₀) = d(Ax₀, Ay₀)  d(x₀, y₀) < d(x₀, y₀) и мы получили противоречие.

Метод отыскания решения уравнения, предложенный в теореме о сжимающих отображениях, называется методом итераций.

Принцип сжимающих отображений имеет многочисленные приложения при доказательствах существования решения и его отыскания. Мы приведем лишь три достаточно важных применения.

1. Задача Коши: Найти решение дифференциального уравнения y = f(x, y) с начальным условием y(x₀) = y₀.

На функцию f (х, у) наложим следующие условия: f(х, у) определена и непрерывна в некоторой открытой области G, которой принадлежит точка (х₀, у₀), и удовлетворяет в этой области условию Липшица по у, т.е.

|f(x, y₁) - f(x, y₂)|  M|y₁ -y₂|.

Теорема 15 (Пикара). В приведенных выше условиях существует такое d > 0, что поставленная задача Коши на отрезке |x - x₀|  d имеет единственное решение у = (х).

Доказательство. Поставленная задача Коши очевидно эквивалентна следующему интегральному уравнению

(х) = у₀ +

В силу непрерывности функции f(х, у) имеем |f(x, y)|  K в некоторой замкнутой ограниченной области D  G, для которой точка (х₀, у₀) является внутренней точкой. Выберем d > 0 так, чтобы выполнялись условия:

1. (х, у)  D, если |х - х₀|  d, |y - y₀|  Kd;

2. Md < 1.

Достаточно очевидно, что эти условия можно удовлетворить. Рассмотрим множество Х – непрерывных функций (х), определенных на отрезке |x - x₀|  d и таких, что |(x) - y₀|  Kd с метрикой d(₁, ₂) = max |₁(x) - ₂(x)|, где максимум ищется на отрезке [x₀ - d, x₀ + d]. Несложно видеть, что Х является замкнутым множеством в пространстве С[x₀ - d, x₀ + d] и следовательно является полным метрическим пространством. Рассмотрим на этом пространстве Х отображение  = А, определяемое равенством

(х) = у₀ +

Это отображение переводит пространство Х в себя и является сжатым. Действительно, если Х, |x - x₀|  d, то |(x) - y₀| =  Kd. Последнее означает, что (х) = (А)(х) Х. Далее, по условию Липшица,

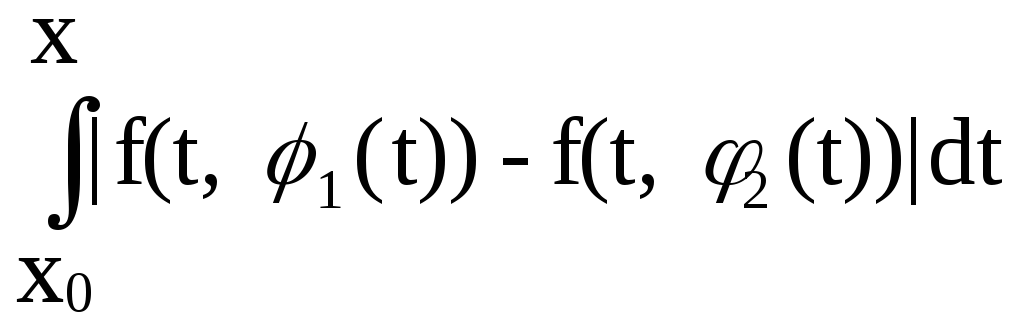
|₁(x) - ₂(x)|   Md|₁(х) - ₂(х)|.

В силу предположений Md < 1 и оператор А является сжимающим. Тогда по принципу сжимающих отображений уравнение (х) = (А)(х), а с ним и исходная задача Коши, имеет единственное решение в пространстве Х.

2. Решение систем линейных алгебраических уравнений методом итераций. Рассмотрим n - мерное пространство R_n. Если R_n,  R_n, то положим . Нетрудно видеть, что определённое так метрическое пространство R_n будет полным. Рассмотрим в этом пространстве отображение Ax = y, заданное с помощью равенств

, i=1, … , n.

Тогда получаем

Если теперь предположить, что <1 для всехi, то мы окажемся в условиях применимости принципа сжатых отображений и, следовательно, отображение будет иметь единственную неподвижную точку. Таким образом, мы получили теорему.

Теорема 16. Если матрица такова, что<1 для всехi, то система уравнений

i=1, 2, … , n,

имеет единственное решение

Это решение можно получить методом итераций, исходя из произвольного вектора .

Условие теоремы 16 есть достаточное условие сходимости метода итераций для рассматриваемой системы. Если в R_n ввести другую метрику, то получим другое условие сходимости. Пусть, например, . При такой метрике

Поэтому условием сходимости метода итераций будет на этот раз неравенство

.

Нетрудно видеть, что полученные здесь условия существования и единственности решений для систем линейных уравнений, могут быть распространены достаточно легко на случай бесконечных систем линейных уравнений в соответствующих метрических пространствах.

3. Интегральное уравнение Фредгольма. Применим теперь принцип сжимающих отображений для разрешимости так называемого неоднородного линейного интегрального уравнения Фредгольма второго рода:

f(x) = + (x).

Здесь К(х, у) - называется ядром интегрального оператора, (x) - заданная функция,  - произвольный параметр, f(х) - искомая функция.

Предположим, что К(х, у) и (x) - непрерывные функции при a  x  b, a  y  b. Тогда в силу теоремы Кантора |K(x, y)|  M. Рассмотрим отображение Аf в метрическом пространстве C[a, b], задаваемое равенством:

(Af)(x) = + (x).

Следующие неравенства вполне очевидны:

d(Af₁, Af₂) = |(Af₁)(x) - (Af₂)(x)|  ||M(b - a) |f₁(x) – f₂(x)|.

Следовательно, при || <1/M(b - a) отображение А является сжимающим в пространстве C[a, b]. В силу принципа сжимающих отображений заключаем, что интегральное уравнение Фредгольма при || <1/M(b - a) имеет единственное решение, которое можно получить методом итераций по формуле:

f_n(x) = + (x).

В этой формуле в качестве начального приближения f₀(х) можно взять нулевую функцию.