5. Критерии компактности в пространствах с[0, 1], lp. Теорема Арцела

Приведем критерии компактности в конкретных метрических пространствах.

Определение 12. Множество M непрерывных на отрезке [0, 1] функций называется равномерно ограниченным, если C: |x(t)|  C, t[0, 1], xM.

Определение 13. Множество M непрерывных на отрезке [0, 1] функций называется равностепенно непрерывным, если для >0 ()>0: |t₁ - t₂| < , t₁, t₂[0,1]  |x(t₁) - x(t₂)|<,xM.

Теорема 5 (Арцела). Множество M  C[0, 1] - относительно компактно  1)М - равномерно ограниченно, 2)М – равностепенно непрерывно.

Необходимость. Положим  = 1 и построим для этого  конечную -сеть x₁(t),..., x_n(t)  C[0, 1] для множества М. Тогда S(x_k(t), 1)  M. Для любого yМ S(x_k(t), 1) найдется такое m, 1 m n, что d(y, x_m(t))<1. Следовательно, |y(t) – x_m(t)| < 1 и |y(t)|  |x_m(t)| + 1. Так как существует С такое, что |x_k(t)|  C для любого k = 1, 2, 3,..., n, то |y(t)|  C + 1. В силу произвольности уМ в этом неравенстве и так как правая часть последнего неравенства от выбора этого у не зависит, мы получим равномерную ограниченность множества функций из М.

Возьмем теперь  > 0 произвольно и также построим конечную -сеть, {x_k(t)}, k=1, 2,..., n. Для конечного набора функций {x_k(t)} в силу его конечности и равномерной непрерывности каждой из функций можно указать такое >0, что из |t₁ – t₂| < , t₁, t₂[0, 1]  |x_k(t₂) – x_k(t₂)| <  для любого k = 1, 2, ..., n. Возьмем произвольное хМ. Тогда m такое, что |x(t) – x_m(t)| <  для t[0, 1]. В силу неравенств

|x(t₁) – x(t₂)|  |x(t₁) – x_m(t₁)| + |x_m(t₁) – x_m(t₂)| + |x_m(t₂) – x(t₂)| <  +  +  = 3

для |t₁ – t₂| < , t₁, t₂  [0, 1], следует, что |x(t₁) – x(t₂)|  3, если |t₁ – t₂| < , t₁, t₂ [0, 1]. Этим показана равностепенная непрерывность функций из множества М.

Достаточность. Пусть множество функций M  C[0, 1] - равномерно ограничено и равностепенно непрерывно. Построим для М компактную -сеть. По предположению о равностепенной непрерывности множества М для  >0  >0: из |t₁ – t₂|<  |x(t₁) – x(t₂)| <  для х  M. Подберем натуральное число n так, чтобы 1/n <  и разобьем отрезок [0, 1] на n равных частей. Для каждой функции х  M поставим ей в соответствие набор чисел (х(0), х(1/n), х(2/n), ..., х(1)). Этим построено отображение функций множества М в вектор (x₁, x₂,..., x_n+1)  R_n+1. Рассмотрим множество M_n+1 = {(x₁,..., x_n+1)  R_n+1: хM: (х(0), х(1/n), х(2/n),..., х(1)) = (x₁, x₂, x₃,..., x_n+1) }. Так как |х(t)|M,t[0, 1], хM, то |x_k|  C для k = 1, 2,..., n + 1, т.е. множество M_n+1 – ограничено в R_n+1, а значит относительно компактно в R_n+1.

Построим множество кусочно-линейных функций M_кл по множеству M_n+1. Именно, для (x₁, x₂, x₃,..., x_n+1)M_n+1 полагаем х_кл(t) = n(t - k/n)(x_k+2 - x_k+1) + x_k+1, при t[k /n, (k + 1)/n], k = 0, 1, 2, …, n – 1. Геометрически последнее означает, что мы соединяем точки (k/n, х_k+1) и ((k+1)/n, х_k+2) отрезком прямой. Вычислим расстояние между двумя функциями из M_кл в метрике пространства С[0, 1]. Имеем

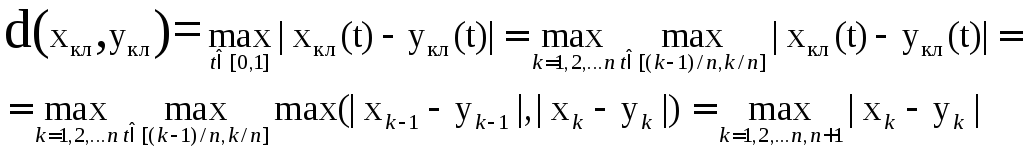
При этом второе равенство выполняется, так как разность линейных функций на отрезке достигает своих меньших и больших значений на концах отрезка. Этим мы установили изометрический изоморфизм между метрическими пространствами М_n+1 с метрикой d_(x, y) = |x_k – y_k| и M_кл с метрикой пространства С[0, 1].

Пусть х⁽ⁿ⁾ M и х⁽ⁿ⁾_клM_кл - построенные по х⁽ⁿ⁾ указанным выше способом кусочно-линейные функции. Так как множество М_n+1 является ограниченным в R_n+1 и следовательно относительно компактным, а сходимость по метрике в R_n+1 эквивалентна сходимости по метрике d_(x, y) = max_k |x_k – y_k| (покажите это), то и множество M_кл также является относительно компактным в C[0, 1]. Для завершения доказательства покажем, что М_кл компактная -сеть для множества М.

В силу равностепенной непрерывности и выбора n из t₁, t₂[(k–1)/n, k/n] следует, что |x(t₁) – x(t₂)| <  для х  M. Пусть для определенности на концах отрезка x((k–1)/n)  x(k/n). Последнее означает, что функция x_кл(t) возрастает на отрезке [(k–1)/n, k/n]. Тогда – < x(t) – x(k/n)  x(t) – x_кл(t)  x(t) – x((k–1)/n) <  для любого t[(k–1)/n, k/n]. Таким образом, ,d(x(t), x_кл(t))<  и М_кл компактная -сеть для М. Теорема доказана.

Теорема 6. Множество M  l_p (1  p < ) - относительно компактно тогда и только тогда, когда 1) множество M - ограничено, 2) для >0  N(): < для nN,xM.

Необходимость. Необходимость 1) условия очевидна. Докажем второе условие. Пусть y⁽¹⁾, y⁽²⁾,..., y^(r) - конечная /2 - сеть для множества М. В силу конечности этого набора для >0  N(): </2 для nN, m = 1, 2,..., r. Тогда для произвольного хM выберем у^(m) так, что d(x, y^(m)) < /2. В результате имеем:   d(x, y^(m)) + /2 < . Получаем необходимое неравенство.

Достаточность. Пусть х = (х₁, х₂,..., х_m, x_m+1, x_m+2,..) и P_mx = (x₁, x₂,..., x_m, 0, 0,...), Q_mx = x - P_mx. По условиям теоремы для >0  m: d(Q_nx, 0)<, nm, xM. Множество M_m = {P_mx, xM} является изометрически изоморфным ограниченному множеству в R_m, следовательно, оно относительно компактно. Тогда для xM , Р_mxM_m и d(x, P_mx) = d(Q_mx, 0)<. Отсюда М_m - компактная -сеть для М, следовательно М -компактно. Теорема доказана.