Глава 2 свойства метрических пространств

1. Сходящиеся последовательности в метрических пространствах и полные метрические пространства

В метрическом пространстве вводится понятие сходимости последовательности. Пусть (Х, d) – метрическое пространство.

Определение 1. Говорят, что x_nХ сходится к xХ (x_n  x; ), если d(x_n, x)  0 при n  .

Понятие сходимости можно сформулировать и на языке «-n». Для   > 0  n₀(): для  n  n₀ справедливо неравенство d(x_n, x) < .

Лемма 1. Если последовательность в метрическом пространстве сходится, то ее предел единственный.

Доказательство. Пусть х_n  а, х_n  b. Применяя неравенство треугольника, получим: d(а, b)  d(а, х_n) + d(х_n, b). Оба слагаемых в правой части стремятся к нулю. Так как d(а,b) неотрицательное и не зависит от n, то по известным теоремам о переходе к пределу в неравенствах получаем d(а,b) = 0, а тогда по свойствам метрики а = b, что и требовалось доказать.

Определение 2. Последовательность х_n элементов метрического пространства Х называется ограниченной, если существует шар S(y, r), которому принадлежат все члены последовательности.

Лемма 2. Если последовательность сходится в метрическом пространстве, то она ограничена.

Доказательство. Утверждение легко вытекает из определения сходящейся последовательности, если заметить, что если х_n  х, то для  фиксированного  > 0 найдется n₀, для которого x_nS(x, ) для всех n  n₀. Следовательно, все члены последовательности за исключением конечного числа попадают в окрестность S(x, ). Так как любой конечный набор элементов является всегда ограниченным, отсюда уже следует ограниченность всей последовательности.

Следствие. Если последовательность {x_n} точек из X сходится к точке xX, то числа d(x_n, y) ограничены для любой фиксированной точки у пространства X.

Лемма 3. Если x_n → x, y_n→ y, то d(x_n, y_n) → d(x, y) (иначе говоря, метрика является непрерывной функцией своих аргументов).

Доказательство. По неравенству четырёхугольника

|d(x, y) - d(x_n, y_n)| d(x, x_n) + d(y, y_n).

Отсюда предельным переходом при n → легко получаем утверждение леммы.

В метрическом пространстве предельными для множества являются такие точки х₀, для которых существует последовательность точек х_n множества сходящаяся к х₀. Замкнутый шар S[a, r] есть замкнутое множество. В самом деле, пусть x_n S[a, r] и x_n → x₀. Тогда d(x_n, a) r, и при n →это неравенство в пределе даетd(x₀, a) r, т.е. х₀S[a, r]. А так как каждая предельная точка шара есть предел некоторой последовательности точек шара, то замкнутость шара доказана.

Выясним конкретный смысл сходимости в метрических пространствах R_n, C[a, b], l₂ и m.

Пример 1. Пусть Х = R_n. Если х_к→х₀, где х_к ={ξ₁^(к),…, ξ_n^(к) } и х₀ ={ξ₁⁽⁰⁾,…, ξ_n⁽⁰⁾ }, то

d(х_к, х₀) = →0 при к → ∞.

Но в силу несложно проверяемых неравенств

,

верных для любого i, это возможно тогда и только тогда, когда ξ_i^(k) → ξ_i⁽⁰⁾_, i = 1,..., n, при k → ∞.

Отсюда следует, что сходимость в R_n есть сходимость координат точек последовательности к соответствующим координатам точки – предела, т.е. сходимость в R_n есть сходимость по координатам.

Пример 2. Пусть Х = C[a, b]. Если {x_n(t)} C[a, b] сходится к х₀(t) C[a, b], то

d(х_n, х₀) = |x_n(t) – x₀(t)| → 0

или иначе: ε >0N:n > N => |x_n(t) – x₀(t)|< ε. Это условие эквивалентно условию, что n > N => |x_n(t) – x₀(t)|< ε t[a, b]. Но это означает равномерную сходимость последовательности {x_n(t)} к х₀(t). Таким образом, сходимость в пространстве С[a, b] есть равномерная сходимость функциональной последовательности {x_n(t)}.

Пример 3. Пусть Х = l₂. Можно показать ,что сходимость последовательности {x_n} l₂ к х₀ l₂, где х_n ={ξ_i⁽ⁿ⁾ }, х₀ ={ξ_i⁽⁰⁾ } означает, что

1) ξ_i⁽ⁿ⁾ → ξ_i⁽⁰⁾ для i = 1,2,...

2) ε>0N:<ε для всех n =1,2,.....

Таким образом, сходимость в l₂ содержит в себе более сильные требования, чем сходимость по координатам. Покажем это на примере, показывающем, что в l₂ сходимость по координатам не влечёт сходимости последовательности точек в l₂.

Возьмем в пространстве l₂ последовательность e_m ={ξ_i^(m)}, где ξ_i^(m)= δ_mi (символ Кронекера). Берём х₀ = (0, 0,…, 0,…) l₂. Тогда последовательность {e_m} по координатам стремиться к точке х₀. Однако d(e_m, x₀) = 1, следовательно {e_m} не стремится к х₀ по метрике.

Пример 4. Пусть X = m. Сходимость последовательности х_n = {ξ₁⁽ⁿ⁾,…, ξ_n⁽ⁿ⁾,…} m к элементу х₀ ={ξ₁⁽⁰⁾,…, ξ_n⁽⁰⁾, …} означает равномерную сходимость по координатам, т.е.  ε>0 N: n > N  | ξ_i⁽ⁿ⁾ – ξ_i⁽⁰⁾ | <ε  i = 1,2,... Доказывается это также как в примере 2.

Можно показать, что в метрическом пространстве s всех числовых последовательностей сходимость по метрике совпадает со сходимостью по координатам.

Определение 3. Последовательность x_nX называется фундаментальной последовательностью, если для  > 0  N: d(x_n, x_m) < , если n, m N.

Лемма 4 (о сходимости последовательностей). Пусть {x_n} – последовательность из метрического пространства Х. Следующие условия эквивалентны:

1. {x_n} – сходится к х;

2. Любая подпоследовательность {x_n} сходится х;

3. Для любой подпоследовательности {} существует подпоследовательность {} сходящаяся кх;

4. {x_n} – фундаментальная и любая подпоследовательность {} сходится кх;

5. {x_n} – фундаментальная и существует подпоследовательность {}, сходящаяся кх.

Доказательство.

1.  2. и 2.  3. Стандартные утверждения из математического анализа: подпоследовательность сходящейся последовательности сходится к тому же пределу: доказательство абсолютно аналогично.

4.  5. Очевидно.

3.  4. вытекает из 5.  1. Действительно, если 5.  1. уже доказано, то в силу условий п.4. подпоследовательность {} фундаментальна, но по п. 3 у нее существует сходящаяся кх подпоследовательность. Тогда из 5.  1. вытекает, что {} сама сходится к х.

5.  1. Пусть {x_n} – фундаментальная последовательность и – ее сходящаяся кх подпоследовательность. Для   > 0  N₁: d(x_p, x_m) < , p, m > N₁. Полагая здесь m = n_k, n_k  N₁, k  N, имеем d(x_p, ) <. Следовательно, d(x, x_p)  d(x, ) + d(,x_p)  +  2 (p > N₁) и x_p  x  Х.

Определение 4. Метрическое пространство Х называется полным, если любая фундаментальная последовательность в этом пространстве сходится к элементу этого пространства.

Пример 5. Для случая R_n – евклидова n–мерного пространства – полнота следует из критерия Коши существования предела последовательности точек этого пространства.

Пример 6. Рассмотрим введенное выше пространство С[0, 1]. По определению фундаментальной последовательности {x_n} и метрики для  >0 N: < n, m  N. Если мы зафиксируем t, то х_n(t) будет обычной числовой фундаментальной последовательностью, у которой существует в силу критерия Коши поточечный предел х(t). Переходя к поточечному пределу в неравенстве верном для любогоt  [0, 1] при m   получаем   для  n  N. Таким образом, последовательность х_n(t) равномерно на отрезке [0, 1] сходится к функции х(t). Тогда по теореме Вейерштрасса о непрерывности равномерного предела непрерывных функций x(t) - непрерывная на отрезке [0, 1] функция. Отсюда C[0, 1] является полным пространством.

Пример 7. На множестве C[0, 1] можно ввести другую метрику, например:

d(x, y) =

но в этом случае пространство не будет полным. Для доказательства этого достаточно рассмотреть следующую последовательность непрерывных функций:

х_n(t) =

Покажите, что эта последовательность фундаментальна по приведенной метрике (используйте геометрический смысл определенного интеграла), но сходится к разрывной функции.

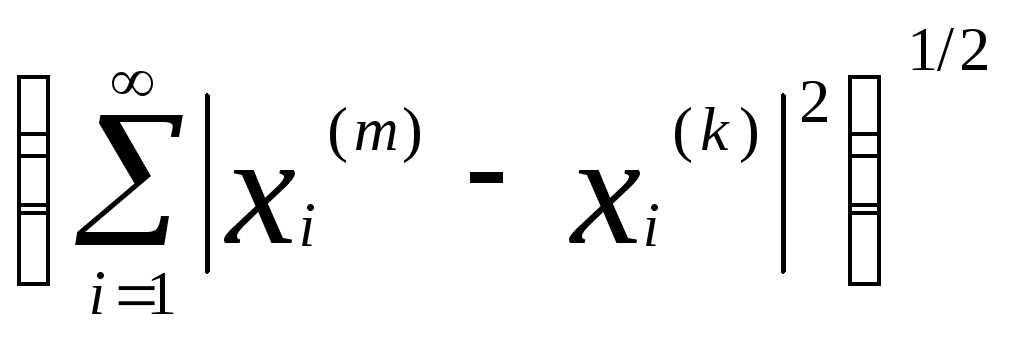Пример 8. Покажем полноту пространства l₂. Пусть последовательность х^(m) = (x₁^(m), x₂^(m),..., x_n^(m),....), m = 1, 2, .... является фундаментальной в l₂. Следовательно, для произвольно выбранного  > 0 существует такой номер n₀, что для всех k, m  n₀ выполняется неравенство <. Из неравенства |x_n^(m) - x_n^(k)|  , верного для любогоn  N, вытекает фундаментальность последовательности {x_n^(m)} в пространстве R и следовательно ее сходимость x_n^(m)  х_n при m . Переходя в очевидном неравенстве

< 

при фиксированном m к пределу сперва при k , затем при p , получим неравенство

 .

Из неравенства треугольника

вытекает принадлежность х к l₂. Из предыдущего же неравенства вытекает сходимость х^(m) к х в l₂.