
Моделирование систем / Моделирование систем / Теория / Шпоры
.docx|
№1. Понятие системы. Системой называется некая совокупность элементов, обособленная от окружающей среды и взаимодействующая с ней как некое целое. Важной особенностью системы является невозможность выполнения отдельными элементами ее функций. Данная особенность получила наименование эмерджентности. Чем сложнее система, чем больше различие между ней и составляющими ее элементами. В системах управления любого типа выделяют следующие составные элементы множество входных сигналов X, множество выходных сигналов Y и каналы воздействия на систему возмущений V (см. рис.1.1). В формализованном виде в данные множества могут быть представлены как: X={x1,x2,…,xi} (1.1) Y={y1,y2,…,yi} (1.2) V={v1,v2,…,vi} (1.3)
4.Информация и ее меры. Информация – это некоторая упорядоченная последовательность сообщений, отражающих, передающих и увеличивающих наши знания. Информация актуализируется с помощью различной формы сообщений – определенного вида сигналов, символов. Информация – содержание сообщения, сообщение – форма информации . 1 бит (binary digit – двоичное число) = 0 или 1, 1 байт 8 бит, 1 килобайт (1Кб) = 213 бит, 1 мегабайт (1Мб) = 223 бит, 1 гигабайт (1Гб) = 233 бит, 1 терабайт (1Тб) = 243 бит, 1 петабайт (1Пб) = 253 бит, 1 эксабайт (1Эб) = 263 бит. Измерение: Наименьшее решение этого неравенства или мера разнообразия множества состояний системы задается формулой Р. Хартли: Если во множестве X = {x1, x2, ..., xn} искать произвольный элемент, то для его нахождения (по Хартли) необходимо иметь не менее logan (единиц) информации. Уменьшение Н говорит об уменьшении разнообразия состояний N системы. Мера Хартли подходит лишь для идеальных, абстрактных систем, так как в реальных системах состояния системы неодинаково осуществимы (неравновероятны). Для таких систем используют более подходящую меру К. Шеннона. Мера Шеннона оценивает информацию отвлеченно от ее смысла:
где n – число состояний системы; рi – вероятность (относительная частота) перехода системы в i-е состояние, а сумма всех pi должна равняться 1.
5.Информационная модель процесса управления Управление - это целенаправленная актуализация знаний. Управление и особая форма - самоуправление, - высшая форма актуализации знаний. Управление в системе - внутренняя функция системы, осуществляемая независимо от того, каким образом, какими элементами системы она должна выполняться. Управление системой - выполнение внешних функций управления, обеспечивающих необходимые условия функционирования системы (см. рис. 7.1).
Рис.7.1. Общая схема управления системой Управление системой (в системе) используется для различных целей:
Как правило, эти цели интегрируются. Управление любой системой (в любой системе) должно подкрепляться необходимыми ресурсами - материальными, энергетическими,информационными, людскими и организационными (административного, экономического, правового, гуманитарного, социально-психологического типа). Управление - непрерывный процесс, который не может быть прекращен, ибо движение, поток информации в системе не прекращается. Цикл управления любой системой (в любой системе) таков: { сбор информации о системе обработка и анализ информации получение информации о траектории выявление управляющих параметров определение ресурсов для управления управление траекторией системы } Основные правила организации информации для управления системой:
Если число возможных состояний системы S равно N, то общее количество разнообразия системы (мера выбора в системе ) равно V(N)=log2N. Пусть управляемая система обладает разнообразием V(N1), а управляющая - V(N2). Цель управляющей системы - уменьшить значение V(N1) за счет изменения V(N2). В свою очередь, изменение V(N1), как правило, влечет изменение и V(N2), а именно, управляющая система может эффективно выполнять присущие ей функции управления лишь при условии, если верно неравенство V(N2) >= V(N1). Это неравенство выражает принцип Эшби (необходимого разнообразия управляемой системы): управляющая подсистема системы должна иметь более высокий уровень организации (или большее разнообразие, больший выбор), чем управляемая подсистема, т.е. многообразие может быть управляемо (разрушено) лишь многообразием. Функции и задачи управления системой:
Планирование (координация во времени, в пространстве, по информации) Асимптотическая устойчивость системы состоит в возврате системы к равновесному состоянию при t∞ из любого неравновесного состояния. Пример. Известная игрушка "Ванька-встанька" - пример такой системы. Пусть система S зависит от вектора факторов, переменных x=(x1,x2,...,xn). Матрицей системы назовем матрицу E=||eij|| из 1 и 0: eij=1 лишь тогда, когда переменная xiоказывает влияние на xj. Связная устойчивость состоит в асимптотической устойчивости системы при любых матрицах Е.
9.Универсальный язык моделирования систем UML, конечные автоматы Объектная методология позволяет выполнить не только анализ предметной области, но и моделирование функционирования программного обеспечения и структуры информационных систем. Причем применяться как процедура анализа, так и процедура синтеза. В качестве нотации — графического языка может использоваться унифицированный язык моделирования UML (Unified Modeling Language). Язык UML позволяет с помощью определенного набора диаграмм, документировать модели информационных систем и ПО. В общем случае конечный автомат представляет динамические аспекты моделируемой системы в виде ориентированного графа, вершины которого соответствуют состояниям, а дуги - переходам. При этом поведение моделируется как последовательное перемещение по графу состояний от вершины к вершине по связывающим их дугам с учетом их ориентации. Для графа состояний системы можно ввести в рассмотрение специальные свойства. Среди таких свойств - выделение из всей совокупности состояний двух специальных: начального и конечного. Ни в графе состояний, ни на диаграмме состояний время нахождения системы в том или ином состоянии явно не учитывается, однако предполагается, что последовательность изменения состояний упорядочена во времени. Другими словами, каждое последующее состояние может наступить позже предшествующего ему состояния.
10.Этапы имитационного моделирования систем. Имитационно компонентное моделирование (ИМКМ) сводится к замещению реального объекта программной моделью и проведению эксперимента с этой моделью. В AnyLogic используется технология объектного моделирования. № Этап Описание 1 Понимание системы Понимание того, что происходит в системе, подлежащей анализу, какова ее структура, какие процессы в ней протекают 2 Формулировка цели моделирования системы
Список задач, которые предполагается решить с помощью будущей модели. Список входных и выходных параметров модели, список исходных данных, критерии завершенности будущего исследования
3 Разработка концептуальной структуры модели
Структура модели, состав существенных процессов, подлежащих отображению в модели, зафиксированный уровень абстракции для каждой подсистемы модели (список допущений), описание управляющей логики для подсистем
4 Реализация модели в среде моделирования
Реализованные подсистемы, их параметры и переменные, их поведение, реализованная логика и связи подсистем
5 Реализация анимационного представления модели Анимационное представление модели, интерфейс пользователя 6 Проверка корректности реализации модели
Убеждение в том, что м дель корректно отражает те процессы реальной системы, которые требуется анализировать 7 Калибровка модели
Фиксация значений параметров, коэффициентов уравнений и распределений случайных величин, отражающих те ситуации, для анализа которых модель будет использоваться 8 Планирование и проведение компьютерного эксперимента Результаты моделирования - графики, таблицы и т. п., дающие ответы на поставленные вопросы
13.Модель черного ящика и нелинейные регрессионные модели. Нелинейные регрессионные модели Квадратичная модель Пусть белый, черный ящик имеет два входа (см. рисунок 8.6), а зависимость выхода от входов напоминает квадратичную, то целесообразно выбрать такую гипотезу: Y=A0+A1·X1+A2·X2+A3·X1·X2+A4·X1·X1+A5·X2·X2.
Рис.8.6. Модель черного ящика с двумя входами Обозначим: Z1=X1·X2 Z2=X1·X1; Z3=X2·X2 и подставим эти выражения в предыдущую формулу: Y = А0 + А1· Х1 + А2· Х2+А3 ·Z1+A4·Z2+A5· Z3. Таким образом, данная задача сведена к линейной множественной модели. А модель черного ящика теперь выглядит так, как показано на рисунке 8.7.
Рис. 8.7. Преобразованная модель черного ящика Мультипликативная регрессионная модель Пусть модель черного ящика имеет вид, показанный на рисунке 8.8. Выход черного ящика связан со входом в виде зависимости: Y=A0·X1A1·X2A2…XmAm Модель черного ящика показана на рисунке 9.3.
Рис.8.8. Модель черного ящика с несколькими входами прологарифмируем левую и правую части данного уравнения: ln(Y)=ln(A0)+A1·ln(X1)+A2·ln(X2)+…+Am·ln(Xm) Обозначим: W=ln(Y),B0=ln(A0),Z1=ln(X1),Z2=ln(X2),…,Zm=ln(Xm) Получим: W=B0+A1·Z1+A2·Z2+…+Am·Zm Обратная регрессионная модель Y=k/(A0+A1·X1+…+Am·Xm) Заменим: W=1/Y, a1=Ai/k Переход к линейной множественной модели W=a0+a1·X1+…+am·Xm Экспоненциальная модель Y=eB0+B1·X1+B2·X2+…+Bm·Xm Прологарифмируем левую и правую части уравнения: ln(Y)=B0+B1·X1+B2·X2+…+Bm·Xm Выполним замену W=ln(Y) и получим: W=B0 + B1·X1 + B2·X2+...+Bm·Xm
15. Классификация экспериментов Теория предполагает, что эксперимент может быть пассивным и активным. При пассивном эксперименте информация об исследуемом объекте накапливается путем пассивного наблюдения, то есть информацию получают в условиях обычного функционирования объекта. Активный эксперимент проводится с применением искусственного воздействия на объект по специальной программе. При пассивном эксперименте существуют только факторы в виде входных контролируемых, но неуправляемых переменных, и экспериментатор находится в положении пассивного наблюдателя. Различные виды экспериментов схематично представлены на рисунке 9.2.
Однофакторный пассивный эксперимент проводится путем выполнения n пар измерений в дискретные моменты времени единственного входного параметра X и соответствующих значений выходного параметра Y (см. рисунок 9.2). Аналитическая зависимость между этими параметрами вследствие случайного характера возмущающих воздействий рассматривается в виде зависимости математического ожидания Y от значения X, носящей название регрессионной. Целью однофакторного пассивного эксперимента является построение регрессионной модели - установление зависимости y=f(x).
Многофакторный пассивный эксперимент проводится при контроле значений нескольких входных параметров Xi (см. рисунок 9.3) и его целью является установление зависимости выходного параметра от двух или более переменных y=F(x1,x2,…) .
Полный факторный эксперимент предполагает возможность управлять объектом по одному или нескольким независимым каналам (см. рисунок 9.4). В схеме используются следующие группы параметров:
{[[[[ При многофакторном и полном факторном эксперименте выходных параметров может быть несколько. Управляющие параметры xi представляют собой независимые переменные, которые можно изменять для управления выходными параметрами. Если i=1 (один управляющий параметр), то эксперимент однофакторный. Многофакторный эксперимент соответствует конечному числу управляющих параметров. Полный факторный эксперимент соответствует наличию возмущающих воздействий в многофакторном эксперименте. Диапазон изменения факторов xi или число значений, которое они могут принимать называется уровнем фактора. Полный факторный эксперимент характеризуется тем, что при фиксированных возмущающих воздействиях Wi минимальное число уровней каждого фактора равно двум. В этом случае, зафиксировав все факторы xi кроме одного, необходимо провести два измерения, соответствующих двум уровням этого фактора. Последовательно осуществляя такую процедуру для каждого из факторов xi, получим необходимое число N опытов в полном факторном эксперименте для реализации всех возможных сочетаний уровней факторов N=2k , где k - число факторов.
18. Описательная статистика и случайная величина. Описательная статистика--Раздел математической статистики – описательная статистика – предназначен для представления данных в удобном виде и описания информации в терминах математической статистики и теории вероятностей. Основной величиной в статистических измерениях является единица статистической совокупности. Единица статистической совокупности характеризуется набором признаков или параметров. Значения каждого параметра или признака могут быть различными и в целом образовывать ряд случайных значений x1, х2, …, хn. Переменная - это параметр измерения, который можно контролировать или которым можно манипулировать в исследовании. Так как значения переменных не постоянны, нужно научиться описывать их изменчивость Относительное значение параметра - это отношение числа объектов, имеющих этот показатель, к величине выборки. Выражается относительным числом или в процентах (процентное значение). Удельное значение данного признака - это расчетная величина, показывающая количество объектов с данным показателем, которое содержалось бы в условной выборке, состоящей из 10, или 100, 1000 и т. д. объектов. Случайная величина (СВ)---- СВ – это численная характеристика, измеряемая по ходу опыта и зависящая от случайного исхода. СВ реализуемая по ходу опыта и сама является случайной. Каждая СВ задает распределение вероятностей. Среднее (оценка среднего, выборочное среднее) — сумма значений переменной, деленная на n (число значений переменной). Если вы имеете значения Х(1), ..., X(N), то формула для выборочного среднего имеет вид:
Выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0. Формально это записывается следующим образом: ( Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения. Выборочная дисперсия вычисляется по формуле: s2
=
Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны. Стандартное отклонение, среднее квадратическое отклонение (от английского standard deviation) вычисляется как корень квадратный из дисперсии. Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего. Математическое ожидание – числовая характеристика СВ, приближенно равная среднему значению СВ: M(x)=x1p1+x2p2+…+xnpn Дисперсия случайной величины D(x)=p1(x1- P1 – Pn – вероятности 21. Стратегическое планирование эксперимента на модели. Планирование эксперимента В планировании эксперимента различают входные (изогенные) и выходные (эндогенные) переменные:х1,х2,…,хк;y1,y2…,ym. Входные переменные в называют факторами а выходные — реакциями. Каждый фактор xi, i=1,2,…,k может принимать в эксперименте одно или несколько значений, называемых уровнями. Фиксированный набор уровней факторов определяет одно из возможных состояний рассматриваемой системы. Одновременно этот набор представляет собой условия проведения одного из возможных экспериментов. Каждому фиксированному набору уровню факторов соответствует определённая точка в многомерном пространстве, называемая факторным пространством. Эксперименты не могут быть реализованы во всех точках факторного пространства, а лишь в принадлежащих допустимой области, как это например оказано для случая двух факторов Х1 и Х2 на рисунке 9.1.
Рис.9.1. Факторное пространство План эксперимента обычно используется для определения экстремальной характеристики объекта. Поэтому планирование эксперимента называется экстремальным. Стратегическое планирование машинных экспериментов с моделями систем Можно выделить стратегическое и тактическое планирование эксперимента на моделях систем. Стратегическое планирование – ставит своей целью получение необходимой информации о системе с помощью модели, реализованной на ЭВМ. Стратегическое планирование машинных экспериментов с моделями систем Можно выделить стратегическое и тактическое планирование эксперимента на моделях систем
23. Модели и их виды. Моделирование - это замещение одного объекта (оригинала) другим (моделью) и фиксация и изучение свойств модели. Замещение производится с целью упрощения, удешевления, ускорения изучения свойств оригинала. Модель - это тоже система со своими множествами параметров Sm и характеристик Ym. Оригинал и модель сходны по одним параметрам и различны по другим. Замещение одного объекта другим правомерны, если интересующие исследователя характеристики оригинала и модели определяются однотипными подмножествами параметров и связаны одинаковыми зависимостями с этими параметрами. Физической моделью Физической моделью обычно называют систему, эквивалентную или подобную оригиналу, но возможно имеющую другую физическую природу. Виды физических моделей:
Натуральные модели - это реальные исследуемые системы (макеты, опытные образцы). Имеют полную адекватность (соответствия) с системой оригиналом, но дороги. Квазинатуральные модели - совокупность натуральных и математических моделей. Этот вид используется тогда, когда модель части системы не может быть математической из-за сложности её описания (модель человека оператора) или когда часть системы должна быть исследована во взаимодействии с другими частями, но их ещё не существует или их включение очень дорого, например (вычислительные полигоны, АСУ) Масштабная модель - это система той же физической природы, что и оригинал, но отличается от него масштабами. Методологической основой масштабного моделирования является теория подобия. Аналоговыми моделями называют системы, имеющие физическую природу, отличающуюся от оригинала, но сходные с оригиналом процессы функционирования. Для создания аналоговой модели требуется наличие математического описания изучаемой системы. В качестве аналоговых моделей используются механические, гидравлические, пневматические и электрические системы. Математические модели. Математические модели представляют собой формализованное представление системы с помощью абстрактного языка, с помощью математических соотношений, отражающих процесс функционирования системы. Математические модели можно классифицировать на детерминированные и вероятностные, аналитические, численные и имитационные. Аналитической моделью называется такое формализованное описание системы, которое позволяет получить решение уравнений, описывающих ее работу в явном виде, используя известный математический аппарат. Численная модель характеризуется такими уравнениями, которые допускают только частные решения для конкретных начальных условий и количественных параметров моделей. Имитационная модель - это совокупность описания системы и внешних воздействий, алгоритмов функционирования системы или правил изменения состояния системы под влиянием внешних и внутренних возмущений
26. Дискретно – детерминированные модели (F- схемы) : Автомат Мура. Конечный
автомат
представляет собой объект, который
функционирует в моменты автоматного
времени t0=0,
t1=T0,
t2=2T0
или в конечном виде
Принято различать два типа автоматов автомат Милля и автомат Мурра. Автомат Мура Автомат получил свое наименование по имени математика Эдварда Ф. Мура. По сравнению с автоматом Мили вход такого автомата исключительно зависит от его состояния. При достижении определенного состояния формируется выходное значение, которое не зависит от перехода в это состояние.
Автомат
описывается кортежем
Когда
автомат после чтения задающего слова
В случае если регулярный язык автомата не имеет значение, множество F может быть исключено из кортежа автомата. Автомат будет определяться кортежем, состоящим из шести элементов. Под регулярным языком автомата понимают формальный язык, который отвечает определенным ограничениям. Число состояний автомата Мура больше по сравнению с числом состояний соответствующего автомата Мили. Пример автомата Мура Пусть
задан детерминированный автомат
кортежем из шести элементов
Работу автомата покажем в виде графа
Рис.. Перевод автомата Мура в автомат Мили. Для перевода на дуге перехода нужно указать дополнительно символ из множества выходных значений целевого состояния.
29.Непрерывно-стохастические модели (Q-схемы). Непрерывно-стохастические модели (Q-схемы) Основные понятия и определения Система массового обслуживания представляет собой класс математических схем, разработанных в теории массового обслуживания и приложений для формализации процессов функционирования систем, которые, по своей сути, являются процессами обслуживания. Характерным для таких объектов является случайное появление требований (заявок) на обслуживание и завершение обслуживания в случайные моменты времени. В любом элементарном акте обслуживания можно выделить две составляющие: 1. ожидание обслуживания 2. обслуживание заявки Процесс обслуживания можно представить в виде прибора обслуживания Пi.
Нi – накопитель ui- поток обслужмвания wi- поток заявок Ki – канал обслуживания заявки.
При моделировании реальных систем используют композиции из отдельных элементарных систем, которые называют Q-схемами. Если каналы отдельных приборов соединены параллельно, то имеет место многоканальное обслуживание, т.е. многоканальная Q-схема. Если приборы и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание, т.е. многофазная Q-схема. Для задания Q-схемы необходимо определить оператор сопряжения он отражает взаимосвязь элементов структуры, т.е. каналов и накопителей между собой. Различают разомкнутые и замкнутые Q-схемы. В разомкнутых Q-схемах обратные связи отсутствуют. В замкнутых Q-схемах есть обратные Q-связи, по которым заявки двигаются в направлении, обратном направлению «вход-выход».
30.Сети Петри - N схемы.Сети Петри. N схемы В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом причинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов. Формальное описание структур таких систем, взаимодействие параллельных систем и процессов может быть получено с помощью сетей Петри ( К. Петри). Сеть Петри представляет собой двухдольный направленный граф. Такой граф состоит из следующих элементов: позиций переходов. Позиции и переходы соединяются между собой направленными дугами. В графе Петри не существует прямых соединений между двумя позициями или двумя переходами. Позиции обозначаются окружностями, переходы показываются в виде прямоугольников. Позиция обладает определенной мощностью и в соответствии с мощностью может содержать несколько знаков (маркеров). Если значение мощности не задано, то оно принимается равной бесконечности или единице. Каждой дуге графа может быть поставлен в соответствие определенный «вес». Если это значение не указано, то принимается значение равное единице. Загрузка позиций маркерами, называется маркировкой и представляет собой состояние сети. Переход считается активным или готовым к активации если во всех входных позициях находится такое число маркеров, которое соответствует весу перехода и все выходные позиции обладают достаточной мощностью – емкостью для того чтобы принять новые маркеры. Переходы готовые к активизации могут, активированы в произвольный момент времени. При включении перехода из входных его входных позиций выбираются маркеры в соответствии с весом дуги и помещаются в выходные позиции в соответствии с весами дуг. Граф N-схемы является мультиграфом, так как он допускает существование кратных дуг от одной вершины к другой.
Рис.. Статическая сеть Петри Пример работы сети Петри Дано сеть. В каждой позиции может находится два маркера. Схема переходов показана в таблице.
После срабатывания перехода d3 на второй схеме маркировка становится равно M6=M0. 35.Параметры системы массового облуживания и оценка ее эффективности. Оценка производительности СМО осуществляется на базе двух следующих процессов: Количество клиентов в системе (Nt),t>0. Этот процесс показывает, сколько клиентов прибывают в момент времени t в СМО. Величина времени нахождения клиента в системе (Vn)n in N. Случайная переменная Vn обозначает время, которое n-йтый клиент проводит в системе. Для расчета величин характеризующих процессы в СМО могут быть использованы различные методы теории стохастических процессов. Сущность метода сильно зависит от какие законы распределения используются для представления интервалов времени прибытия клиентов и времени обслуживания, какие показатели подлежат расчету: время зависимые или стационарные. Базовая модель СМО достаточно сложна, что даже для известных законов распределения она не имеет точного решения. Однако существуют приближенные формулы, которые хорошо зарекомендовали себя на практике, которые учитывают стохастические особенности процесса функционирования СМО. В стационарном состоянии может быть применена формула Allen-Cunnen, для подсчета числа клиентов.
Здесь
коэффициент загрузки системы,
Оптимальное среднее время нахождения пользователя в системе можно определить по формуле Литтла
Где интенсивность входного потока заявок Исходя из формул, можно выделить следующие зависимости: Средне число клиентов в системе от загрузки прибора обслуживания С увеличением загрузки p увеличивается также число клиентов в системе. Кроме того чем больше коэффициент вариации времени обслуживания, тем больше число среднее число клиентов в системе E[N]
36.Потоки событий в системах массового обслуживания. Многопользовательские информационные системы (ИС) находятся под воздействием неупорядоченного потока событий (запросов, заявок, требований) и поэтому относятся к СМО. Интервалы времени между событиями являются случайными, и плотность вероятности их распределения часто не может быть определена. На практике обычно по статистике получают только средний интервал между соседними событиями. Таким образом, потоком называют последовательность однородных событий со случайными интервалами. Для математического моделирования СМО часто применяют экспоненциальный (показательный) закон распределения интервалов между событиями, плотность вероятности которого при среднем значении а выражается формулой
Этот закон хорошо согласуется со многими реальными процессами и, кроме того, обеспечивает достаточно простые математические преобразования. К такому процессу для потока событий дополнительно предъявляются следующие три требования: • стационарность (характеристики процесса не должен иметь существенных изменений во времени); • ординарность (в один момент времени не должно быть более одного события); • без последействия (будущий процесс зависит только от состояния системы в данный момент и не зависит от пути прихода в это состояние). По последнему требованию процесс определяют как марковский (более точно его можно назвать процессом без предыстории). Поток событий, удовлетворяющий перечисленным выше условиям, называется простейшим или пуассоновским. Простейшие потоки обеспечивают наиболее простое математическое описание. Это обусловлено тем, что при экспонен- циальном законе распределения после появления события в какой - то момент времени интервал до возникновения следующего события остается подчиненным экспоненциальному закону с теми же характеристиками. Этим и обеспечиваются перечисленные выше условия Маркова. Для
потоков вводится характеристика
интенсивности, равная среднему
количеству событий в единицу времени.
Например, если для случайной
последовательности средний интервал
равен z,
то
интенсивность потока будет
Практика показывает, что при слиянии нескольких (более 4-5) независимых произвольных потоков примерно одинаковой интенсивности образуется простейший поток суммарной интенсивности. Если в ИС запросы подают N клиентов со средними интервалами z1,z2,…,zN. Суммарная интенсивность запросов на входе системы обработки
а
средний интервал между запросами
будет следующим
Рассмотрим
пример. Имеется сложный прибор из N
типов
элементов, причем каждый тип содержит
N;
элементов
(i=1...N)
со
средним временем наработки на отказ
ti
,
интенсивность отказов прибора будет
38.Построение модели состояний системы массового обслуживания. Информационные системы имеют конечное число дискретных состояний и их функционирование можно описать с помощью непрерывных марковских цепей. Время пребывания ИС в том или ином состоянии можно описать непрерывной случайной величиной и определить вероятности нахождения системы во всех возможных состояниях. Естественно, сумма вероятностей всех состояний в любой момент времени равна 1. Для решения поставленной задачи составляется граф состояний функционирования ИС. На рис. 2.1 представлен граф системы с тремя возможными состояниями С0, С1 и С2 (вершины графа, обозначены кружками). Вероятности пребывания ИС в этих состояниях являются функциями времени p0(t), р1(t), p2(t), которые и следует определить для анализа функционирования системы. Возможные переходы из состояния в состояние изображены стрелками. Интенсивности таких переходов (все потоки полагаются простейшими) представлены значениями 01,10,12,21,02,20
Получим уравнения динамики состояний ИС. Пусть в момент t система находится в состоянии С0 с вероятностью p0(t). Через интервал t для состояния С0 возможны вероятности вариантов: 1) остаться в С0 p0(t+t); 2) выход из состояния С0 в состояния С1 или С2 p0(t)[-01-02] t; 3)переход в С0 из других состояний p1(t)10t+p2(t)20t. Таким образом, получим p0(t +t)=p0(t)-р0(t)[01+02] t+p1(t)10 t+p2(t)20 t.
Предел
разделенной разности
водит к дифференциальному уравнению первого порядка для вероятности состояния С0
Аналогичным образом могут быть получены уравнения и для других состояний. В конечном итоге для системы с N со стояниями могут быть записаны N обыкновенных дифференциальных уравнений первого порядка:
|
2.Общая классификация систем. Технические системы управления — это системы, которые содержат в качестве элементов технические устройства и могут в течение некоторого интервала времени функционировать без участия человека. Технические системы управления имеют следующие особенности: четко определенную единственную цель управления; отсутствие человека в контуре управления; достаточно высокую определенность исходных данных и возможность формализации процессов функционирования. В технических системах легко выделить объект управления и управляющую систему. Автоматизированные системы управления — это системы, включающие в качестве элементов, как технические системы, так и персонал, взаимодействующий с этими системами. Организационные системы возникают в обществе. В качестве такой системы выступает коллектив людей, деятельность которых сознательно координируется для достижения определенной цели. С развитием вычислительной техники непосредственно связан процесс становления информационных технологий. Информация становится товаром, стратегическим ресурсом. Для автоматизации процесса приема, хранения, обработки и передачи информации был разработан определенный тип автоматизированных информационных систем управления. Автоматизированные информационные системы функционируют в определенной предметной области. При этом предметную область можно определить как сферу интересов пользователей данной системы. Также существует классификация систем по цели использования для обработки информации. АСУ – совокупность технических программных средств и персонала, собранных в единое целое для обеспечения процесса управления в научной, производственной и общественной деятельности. АСУП – АСУ производства (частный случай АСУ). ОАСУ – отраслевая АСУ. АСУТП – АСУ технологическими процессами, обычно является подсистемой в АСУП. ИС – информационные системы, они автоматизируют процесс сбора информации и ее обработку, пользователь этой системы использует получаемую информацию в нужных ему целях. ИС подразделяют на ИПС – информационно-поисковые системы, в них имеется база данных и информационно-поисковый язык (ИПЯ), с помощью которого пользователь формирует требования для извлечения информации. ДИС – документальные ИС, в них хранятся электронные копии документов базы данных. ФИС – фактографические ИС, в них хранятся факты (некоторые записи в БД, в которых зафиксирована информация о явлении в процессе управления). В ФИСах ИПЯ не используется. ЭИС – экспериментальная ИС, в БД таких систем хранятся некие данные и правила обработки информации этих данных, совокупность этой информации образует некоторые знания в предметной области ИС. Пользователь такой системы может получить экспериментальное заключение по интересующим его вопросам.
6.Универсальный язык моделирования UML, структурное моделирование Объектная методология позволяет выполнить не только анализ предметной области, но и моделирование функционирования программного обеспечения и структуры информационных систем. Причем применяться как процедура анализа, так и процедура синтеза. В качестве нотации — графического языка может использоваться унифицированный язык моделирования UML (Unified Modeling Language). Язык UML позволяет с помощью определенного набора диаграмм, документировать модели информационных систем и ПО. При этом различают следующие виды моделирования:
Структурное моделирование Структурное моделирование предусматривает выделение в предметной области определенного набора классов и определения взаимосвязей между ними. В результате формируется диаграмма классов (Static Structure Diagram). Класс UML в общем виде отображается с помощью следующей структуры, показанной на рисунке 1.1.
Атрибуты – это свойства, которые хранят информацию о наиболее существенных характеристиках реального объекта предметной области, выбранные разработчиком. Атрибуты задаются в следующем виде: Доступ Название атрибута: Тип Для указания доступа к атрибутам используются следующие условные обозначения, описанные в таблице 1.2. Таблица. 1.2. Доступ к атрибутам. Условное обозначение Описание - Protected (Закрытый) Доступ к атрибуту возможен только в операциях класса + Public (Глобальный). Атрибут доступен в операциях класса и в любом месте модели, где получен экземпляр класса # Protected (Защищенный). Доступ к атрибуту возможен в любой операции класса и подклассах
Определение операции: Доступ Наименование([параметры]): [Тип Возвращаемого значения] Задание параметров: [Спецификация] Название: Тип Спецификация параметров: in – Принимает значение; out – Возвращает значение; inout – принимает и возвращает значение. На диаграмме классов принято выделять следующие связи: Зависимость: Один объект зависит от описания другого. Если это описание меняется, то следует изменить и зависимый объект (см. рисунок 1.3).
Ассоциация: Один объект содержит другой. В UML объекты, связанные отношением ассоциации, соединяются друг с другом. Ассоциация может быть указана со стрелкой или без нее. В ассоциации допускается указывать роли – место, занимаемое объектом в отношении (см. рисунок 1.4).
Язык UML позволяет отображать множественность (кратность) ассоциации (зависимости). Множественность обозначает возможное количество объектов, участвующих в ассоциации. В таблице 1.3. приводятся кратности ассоциации, а на рисунке 1.5 приводится пример ассоциации между классами с кратностью. Таблица 1.3. Кратности ассоциации.
Агрегирование: Вид ассоциации, используется для моделирования «Целое/Часть» между равноправными классами. Изображается сплошной линией с не закрашенным ромбом на конце (см. рисунок 1.6).
Композиция: Вид ассоциации, моделирующий отношение «Целое/Часть» между неравноправными классами. Часть, находящаяся в отношении композиции с целым, не является независимой от целого. Изображается композиция сплошной линией с закрашенным на конце ромбом на конце соответствующим отношению «Целое/Часть» (см. рисунок 1.7).
Обобщение: Такое отношение отражает связь между общим и конкретным. Представляет собой наследование. При наследовании выделяют родительский класс – суперкласс и подкласс (наследник). Подкласс наследует от суперкласса зачищенные и глобальные атрибуты и операции. Изображается обобщение сплошной линией с не закрашенной стрелкой. Стрелка должна указывать на суперкласс (см. рисунок 1.8).
11.Одномерная модель черного ящика и линейная регрессия. В целях исследований часто бывает удобно представить исследуемый объект в виде ящика, имеющего входы и выходы, не рассматривая детально внутреннюю структуру. По степени информированности исследователя об объекте существует деление объектов на три типа «ящиков»:
Модель черного ящика. Значения на входах и выходах черного ящика можно наблюдать и измерять. Содержимое ящика неизвестно. Регрессионный метод используется для того, чтобы, зная множество значений на входах и выходах, определить структуру системы, либо построить ее модель, которая позволит связать вход и выход. Такая задача называется задачей регрессионного анализа. Результаты наблюдений за объектом имеют вид, показанный на рисунке 8.2. Всего на графике n экспериментальных точек.
Рис.8.2 Экспериментальные точки Предположим, что мы имеем дело с черным ящиком, имеющим один вход и один выход. Допустим, что зависимость между входом и выходом линейная или близка к линейной. Тогда данная модель будет называться линейной одномерной регрессионной моделью. Для проверки сделанного допущения нужно выполнить последовательность действий, которая изложена ниже. 1) Вносится гипотеза о структуре ящика. Рассматривая экспериментально полученные данные, предположим, что они подчиняются линейной гипотезе, то есть выход Y зависит от входа X линейно: y=A1X+A0 2) Определение коэффициентов A0 и A1 модели Линейная одномерная модель модель черного ящика показана на рисунке 8.3.
Рис. 8.3. Гипотеза. Черный ящик с одним входом и выходом Ошибки Ei, для всех n точек наблюдений следует сложить. Чтобы положительные ошибки не компенсировали в сумме отрицательные, каждую из ошибок возводят в квадрат и складывают их значения в суммарную ошибку F уже одного знака:
Цель метода — минимизация суммарной ошибки F за счет подбора коэффициентов A0, A1. Необходимо найти такие коэффициенты A0, A1 линейной функции Y=A1X+A0, чтобы ее график проходил как можно ближе одновременно ко всем экспериментальным точкам. Этот метод называется методом наименьших квадратов. Для нахождения коэффициентов A0, A1 используют матричное уравнение Крамера:
3) Проверка гипотезы. Проверка гипотезы выполняется путем расчета ошибки по формулам
Если
в полосу, ограниченную линиями
Допускается
повышение критерия надежности гипотезы.
В этом случае используют контрольную
полосу, ограниченную линиями
Расстояние S связано с следующим соотношением:
Рассмотренная проверка гипотезы основывается на предположении о нормальном законе распределения случайных ошибок.
16. Матрица планирования эксперимента. Приведем пример планирования эксперимента. Пусть необходимо взвесить на весах три тела разной массы A,B,C при условии, что нулевое положение весов не отрегулировано. При составлении плана эксперимента принято строить матрицу планирования. В таблице 9.1 приведен первый план взвешивания. «1» и «-1» соответствуют наличию или отсутствию объекта на весах. Таблица 9.1 План взвешивания, вариант №1
Эксперимент состоит из четырех опытов. При первом опыте снимаются показания пустых весов, и выставляется их нулевое положение, затем отдельно взвешивается каждый из объектов. Расчет веса и погрешности измерений 2 каждого из тел производится по следующим формулам: Поскольку погрешности независимых измерений складываются, а вес каждого объекта получен в результате двух измерений, погрешность составляет 22. Оптимально будет провести эксперимент по схеме, показанной в Таблице 9.2. В этом случае взвешивается отдельно каждый из объектов и все объекты вместе. Непосредственное измерение погрешности y0 не проводят.
В этом случае выигрыш при проведении эксперимента заключается в том, что масса каждого из объектов вычисляется по новым формулам, а дисперсия результатов оказывается вдвое меньше. Этот результат получается за счет того, что при втором плане эксперимента смещение нуля измерительной аппаратуры (весов) исключено.
Планирование эксперимента позволяет либо уменьшить число измерений, либо увеличить их точность.
19. Параметрические критерии проверки статистической гипотезы. Статистическая гипотеза – это предположение о свойствах случайных величин или событий, которое мы хотим проверить по имеющимся данным. Нулевая гипотеза – это основное проверяемое предположение, которое обычно формулируется как отсутствие различий, отсутствие влияние фактора, отсутствие эффекта, равенство нулю значений выборочных характеристик и т.п. Например: Имеется механическое устройство, выходное звено которого совершает вращательное движение. Гипотеза: увеличение скорости вращения выходного звена не влияет на устойчивость процессов внутри механизма. Другое проверяемое предположение (не всегда строго противоположное или обратное первому) называется конкурирующей или альтернативной гипотезой. Нулевая гипотеза обозначается Н0, а альтернативная как Н1. Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость проверить ее. Так как проверку производят статистическими методами, то данная проверка называется статистической. При проверке статистических гипотез возможны ошибки (ошибочные суждения) двух видов: H0=TRUE H1=FALSE можно отвергнуть нулевую гипотезу, когда она на самом деле верна (так называемая ошибка первого рода); H0=FALSE H1=TRUE можно принять нулевую гипотезу, когда она на самом деле не верна (так называемая ошибка второго рода). Критерий Стьюдента (t-критерий) Случай независимых выборок Статистика критерия для случая несвязанных, независимых выборок равна:
где
где n1 и n2 соответственно величины первой и второй выборки. Если n1=n2, то стандартная ошибка разности средних арифметических будет считаться по формуле:
где n величина выборки. Подсчет числа степеней свободы осуществляется по формуле: k=n1+n2-2 При численном равенстве выборок k = 2n - 2. Далее необходимо сравнить полученное значение tэмп с теоретическим значением t -распределения Стьюдента. Если tэмп<tкрит, то гипотеза H0 принимается, в противном случае нулевая гипотеза отвергается и принимается альтернативная гипотеза. Случай связанных (парных) выборок В случае связанных выборок с равным числом измерений в каждой можно использовать более простую формулу t-критерия Стьюдента. Вычисление значения t осуществляется по формуле:
где
Значение Sd вычисляется по следующей формуле:
Число степеней свободы k определяется по формуле k=n-1. Рассмотрим пример использования t-критерия Стьюдента для связных и, очевидно, равных по численности выборок. Если tэмп<tкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная. Критерий Фишера Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фишера такова:
где
-
Так как, согласно условию критерия, величина числителя должна быть больше или равна величине знаменателя, то значение Fэмп всегда будет больше или равно единице. Число степеней свободы определяется по формуле: k1=n1 - 1 для первой выборки (величина дисперсии которой больше) и k2=n2 - 1 для второй выборки. Если tэмп<tкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная
24. Непрерывно – детерминированные модели. D-Схемы. Рассмотрим систему, обобщенная модель которой показана на рисунке.
Рис.. Система с одним входом и выходом Для описания поведения системы может быть использовано линейное дифференциальное уравнение с постоянными коэффициентами k-го порядка:
Такое уравнение называется уравнением «вход-выход». Решение уравнения (1) зависит: 1) от входного воздействия x(t);
2)
от начальных условий
Введем в рассмотрение переменные состояния:
Начальные условия
:
Сравнивая уравнения (2) и (3) получаем матрицу координат состояния (переменных):
Матрицы
коэффициентов входных воздействий
В общем случае, когда передаточная функция системы имеет вид:
Уравнение (3) можно представить также в виде структурной схемы:
Рис.3. Структурная схема уравнения «вход»-«выход» Утолщенными
стрелками обозначены векторные
величины.
x,y
в уравнение (3) и на данной схеме в общем
случае представляют собой векторы
соответствующих размерностей
Пространство,
координатами которого являются
переменные
При
Дискретные D схемы Такие схемы могут быть представлены в виде разностных уравнений. Пусть система описывается уравнениями
В
уравнениях (1) заменим
Такая система уравнений называется разностной. Разностные уравнения описывают поведение системы в дискретном времени t=0, n, 2n,… n-дискретный шаг моделирования. Пример:
Здесь u вход системы, а x ее выход. На практике требуется записать уравнение в нормальной форме Коши, и пользуясь методом Эйлера перейти к разностным уравнениям. Для перехода к разностным уравнениям по методу Эйлера вводится замена производной в виде:
Значение x[n+1] – это значение на текущем шаге моделирования, а значение x[n] - значение на рассчитанное на предыдущем шаге моделирования. Величина T0 – период дискретизации при обработке уравнения на ЭВМ. Введем условные обозначения: z1=x;z2=x’;z3=x”;
Тогда уравнения производных примут вид:
В окончательном виде:
31. Обобщенные модели (А - схемы). Понятие агрегата Обобщенный (универсальный) подход базируется на понятии агрегативной системы, предложенной Бусленко Н.П. Она представляет собой формальную схему общего вида, которую называют А – схемой. При агрегативном описании моделируемый объект (система) декомпозируется на конечное число подсистем с сохранением связей, которые обеспечивают их взаимодействие. В результате декомпозиции, система представляется в виде многоуровневой конструкции из взаимосвязанных элементов, которые объединяются в подсистемы различных уровней. В качестве элемента А – схемы выступает агрегат. Структура агрегативной системы Последовательность входных сигналов, расположенных в порядке их поступления в А – схему называют входным сообщением или X–сообщением.
Рис.. Пример A схемы Последовательность выходных сигналов упорядоченную относительно времени выдачи называют выходным сообщением или Y–сообщением. Информация, которая циркулирует в А–схеме делиться на внутреннею и внешнюю. Внешняя информация поступает от внешних объектов, а внутренняя вырабатывается агрегатами А–схемы. Обмен информации А–схемы с внешней средой происходит через агрегаты, которые называют полюсами. Различают входные полюсы, на которые поступают X–сообщения и выходные полюсы – это агрегаты, выходная информация которых представляет Y–сообщения.
Упорядоченную
совокупность операторов An
1) Каждый элементарный канал, передающий сигналы во внешнюю среду должен начинаться в одном из выходных контактов одного из агрегатов А-схемы. Каждый элементарный канал, передающий сигнал из внешней среды должен заканчиваться на одном из входных контактов агрегатов А–схемы. 2) Сигналы в А–схеме передаются непосредственно от одного агрегата к другому без устройств, которые могут отсеивать сигналы по каким-либо признакам. 3) Необходимо согласование функционирования агрегатов во времени. 4) Сигналы между агрегатами А–схемы передаются мгновенно без перекодирования и исключения сигнала.
33. Модели системной динамики. В моделях системной динамики основной интерес представляют накопители некоторого содержимого и анализ изменения их объемов во времени. Содержимое накопителей может иметь любую природу. Даже в рамках одной и той же модели одни накопители отражают динамику ресурсов, другие денег, третьи продукта. При создании модели исследователь абстрагируется от природы того, что представлено в накопителях. Если даже содержимое накопителей является дискретным, то на этом наиболее высоком уровне абстракции индивидуальность и даже сама дискретная природа содержимого (будь то материалы, люди, заявки на поставку продукции и т. п.), количественное изменение которых учитывается в модели, игнорируется. Для переменных модели обычно используются вещественные значения. Вне зависимости от конкретного содержимого накопителя, фрагмент структурной схемы рис. 13.2 имеет вполне определенную семантику. Все три представления этого фрагмента — графический, в виде дифференциального и в виде интегрального уравнения являются эквивалентными.
Рис. 13.2. Три эквивалентных представления динамики накопителя Одна из идей Дж. Форрестера состояла в том, чтобы использовать единую метафору и единую терминологию для потоков любой природы в
моделях системной динамики. Пусть мы имеем два бака, соединенных трубопроводом (рис. I3.3). В первый бак наливается жидкость с постоянной скоростью (интенсивностью), из него жидкость течет во второй бак со скоростью, которая является функцией уровней жидкости в первом и втором баке, из третьего бака жидкость вытекает со скоростью, которая является функцией уровня этого бака.
37.Прямая и обратная задача проектирования систем массового обслуживания. Обратная задача ТМО Прямая. Определение E[N], E[V], - в результате эксперимента. В техническом задании на проектирование СМО обычно указываются ограничения на основные показатели эффективности системы, например: среднее время обслуживания s<ps; доля отказов в приёме заявок r<pr; загрузка обрабатывающей части системы q>pq. Всё это надо обеспечить при заданной интенсивности входного потока . В первую очередь следует определиться с производительностью процессоров (), подходящих к требуемым условиям обслуживания. Количество процессоров N и количество мест в очереди М включим в аргументы формул и будем определять их значения, удовлетворяющие поставленным ограничениям. Такой алгоритм и составляет обратную задачу теории массового обслуживания. Показатели эффективности при решении обратной задачи будут иметь вид:
Как видно из формул, в них входят один заданный параметр -интенсивность входного потока заявок и три аргумента: нагрузка, приведенная к производительности одного процессора i, количество процессоров N и количество мест для очереди М.
39.Модель состояний «Зарождение – гибель». ОСОБЕННОСТИ АНАЛИТИЧЕСКОГО МОДЕЛИРОВАНИЯ СМО Имитационное моделирование позволяет просто описывать сложные СМО и дает достаточно точное определение показателей эффективности систем, но требует значительного времени для проведения серии опытов и их статистической обработки. Кроме того, по его результатам сложно решать обратную задачу ТМО. Структура многих СМО, в том числе и информационных систем (ИС), позволяет описывать их функционирование уравнениями, допускающими относи- тельно простое решение обратной задачи ТМО. Так системы с ограниченной очередью имеют конечное число дискретных состояний и их функционирование можно описать процессом с непрерывным временем. Под состоянием понимается количество заявок, находящихся в системе (в очереди и под обработкой). Для описания процессов в системе применяют вероятности состояний, которые в конкретный момент времени определяют вероятности нахождения системы в одном из всех возможных состояний. Для марковских случайных процессов эти вероятности находятся решением системы обыкновенных линей дифференциальных уравнений Колмогорова. Вероятности состояний характеризуют среднюю долю времен в течение которого система находится в данном состоянии. Для решения поставленной задачи составляется граф Функционирования ИС. На рис. 4.1 представлен граф однопроцессорной (одноканальной) системы с пятью возможными состояниями С0, С1, С2, С3 и С4 (эти состояния обозначены в кружках определенными индексами). В данной схеме накопитель имеет M=3 места для очереди, что соответствует М+2 возможным стояниям: отсутствие заявок, одна заявка в обработке, далее заявка в обработке и 1, 2, 3 заявки в очереди. Вероятности пребывания системы в этих состояниях являются функциями времени p0(t),p1(t),…,p4(t) которые можно определить для анализа функционирования системы. Особенность схемы состоит в том, что переходы возможны из одного состояния (если оно не крайнее) Только в соседние состояния. Интенсивность переходов из текущего состояния в состояние с более высоким индексом (вправо) определяется входным потоком заявок и задается постоянным . Интенсивность переходов в состояния с меньшими индексами (влево) определяется производительностью обрабатывающей части и для одного процессора она равна ,
Система, в которой переходы происходят только в соседние соседние состояния, называют «схемой размножения и гибели». Для такой схемы матрица коэффициентов системы дифференциальных уравнений становится трехдиагональной, что существенно упрощает составление и решение системы уравнений. Для марковских Процессов определение финальных вероятностей состояний сводится к решению системы алгебраических уравнений.
|
3.Понятие структуры системы. Важным системным понятием является понятие элемента и структуры. Введем следующие определения: Элементом системы называется ее неделимая часть. Структурой системой называется совокупность ее элементов связанных определенным образом. В общем виде структуру системы можно описать с помощью формулы S={ei,j} (1.4) где i и j изменяются от 1..n; n – число связей в системе. Совокупность элементов системы характеризуется определенным набором параметров состояний, которые изменяются во времени Z={z1,z2,..,zi} (1.5) где Z – множество состояний системы, а zi – значение параметра системы. Если в процессе управления системой параметры состояния должны обладать определенными постоянными значениями, то такое состояние системы называется гомеостазисом. С точки зрения структуры системы говорят о простых системах, сложных системах и больших. Простые системы состоят из определенного набора элементов. Сложные системы состоят из отдельных подсистем, а большие системы это совокупность пространственно распределенных сложных систем. 7. Универсальный язык моделирования систем UML, архитектурное моделирование систем. Архитектурное моделирование Архитектурное моделирование системы выполняется на основе: диаграмм компонентов (Component Diagram); диаграмм развертывания (Deployment Diagram). Основными элементами таких диаграмм являются: компоненты; узлы; интерфейсы. Условные обозначения элементов архитектурного моделирования приведены в таблице 1.6. Таблица 1.6. Условные обозначения.
Компонент представляет собой физическую часть системы. Компонент может представлять собой исполняемый программный код, либо электронный вариант документа. Выделяют 3 типа компонентов.
Кроме этого в языке UML определено пять стандартных стереотипов для компонентов: executable – исполняемый программный код; library – библиотека объектов; table – таблица базы данных; file – документ с текстом программы, данными; document – любой документ, полученный в результате работы программы. Компоненты реализуют некоторый интерфейс. Интерфейс – это объявление сервиса, у которого есть фиксированные правила взаимодействия. Если интерфейс реализуется компонентом, то такой интерфейс называется экспортируемым. Он используется для предоставления услуг другим компонентам. Если компонент использует интерфейс, то он называется импортируемым. Связь с импортируемым интерфейсом отображается в виде зависимости.
Выделяют следующие свойства компонентов: - компонент представляет собой код; - компонент может быть заменен другим, если он совместим с интерфейсом; - компонент может экспортировать несколько интерфейсов; - компонент это часть системы, взаимодействующая с остальными через набор интерфейсов. Узел – это часть системы, которая содержит процессы и память для обработки данных. Моделирование физического развертывания системы выполняется с помощью узлов и связей между ними. Узел должен обладать именем. Узел реализует выполнение компоненты.
8.Универсальный язык моделирования систем UML, моделирование поведения систем. Объектная методология позволяет выполнить не только анализ предметной области, но и моделирование функционирования программного обеспечения и структуры информационных систем. Причем применяться как процедура анализа, так и процедура синтеза. В качестве нотации — графического языка может использоваться унифицированный язык моделирования UML (Unified Modeling Language). Язык UML позволяет с помощью определенного набора диаграмм, документировать модели информационных систем и ПО. При этом различают следующие виды моделирования:
архитектурное моделирование Моделирование поведения системы Моделирование поведения системы средствами UML выполняется путем использования: диаграмм прецедентов (Use Case Diagram); диаграмм активности (Activity Diagram); диаграмм взаимодействия (Sequence Diagram, Collaboration Diagram). Диаграмма прецедентов Прецедент – множество последовательностей действий для получения инициатором действий определенного результата. Инициатор действий это актер. Актер – связанное множество ролей, которые реализуются пользователями системы. В UML используется два стереотипа: include – включение одного прецедента в другой; extend – расширение прецедента.
Рис.1.16. Пример диаграммы прецедентов. Диаграмма активности---Диаграммы активности моделируют динамический аспект поведения системы. Такая диаграмма документирует некую деятельность системы. Деятельность реализует определенную функцию системы. Она состоит из набора состояний. Состояния бывают двух типов: состояния действия; состояния деятельности. Диаграммы взаимодействия-Диаграммы взаимодействия используются для отображения объектов, отношений между ними и сообщений которыми они обмениваются. Диаграммы взаимодействий реализуются в виде: Диаграммы последовательностей (Sequence Diagram); диаграммы кооперации (Collaboration Diagram). Диаграмма последовательностей отображает процесс движения и возникновение сообщений в системе во времени. Диаграмма кооперации отражает структурную организацию объектов порождающих и принимающих сообщения. Сообщение – некоторая совокупность правил обмена данными между объектами. Сообщение предполагает, что объект, получив некоторую информацию, ответит на нее некоторой последовательностью действий. В качестве сообщения может рассматриваться вызов определенной операции объекта с определенным набором исходных данных.
12.Многомерная модель черного ящика и линейная регрессия. Регрессионные модели----Линейные регрессионные модели В целях исследований часто бывает удобно представить исследуемый объект в виде ящика, имеющего входы и выходы, не рассматривая детально ею внутренней структуры. По степени информированности исследователя об объекте существует деление объектов на три типа «ящиков»: «белый ящик»: об объекте известно все; «серый ящик»: известна структура объекта, неизвестны количественные значения параметров; «черный ящик»: об объекте неизвестно ничего. Значения на входах и выходах черного ящика можно наблюдать и измерять. Содержимое ящика неизвестно. Задача состоит в том, чтобы, зная множество значений на входах и выходах, построить модель, то есть определить функцию ящика, по которой вход преобразуется в выход. Такая задача называется задачей регрессионного анализа. В зависимости от того, доступны входы исследователю для управления или только для наблюдения, можно говорить про активный или пассивный эксперимент с ящиком. Результаты наблюдений за объектом имеют вид, показанный на рисунке 8.2. Всего на графике n экспериментальных точек.
Предположим, что мы имеем дело с черным ящиком, имеющим один вход и один выход. Допустим, что зависимость между входом и выходом линейная или близка к линейной. Тогда данная модель будет называться линейной одномерной регрессионной моделью. Для проверки сделанного допущения нужно выполнить последовательность действий, которая изложена ниже. 1) Исследователь вносит гипотезу о структуре ящика. Рассматривая экспериментально полученные данные, предположим, что они подчиняются линейной гипотезе, то есть выход Y зависит от входа X линейно, и гипотеза имеет вид: y=A1X+A0 2) Определение неизвестных коэффициентов A0 и A1 модели Линейная множественная модель Предположим, что функциональная структура ящика имеет линейную зависимость, но количество входных сигналов, действующих одновременно на объект, равно т (см. рис. 8.5):
Рис. 8.5. Черный ящик с несколькими входами Y=A0+A1X1+…+AmXm Так как подразумевается, что мы имеем экспериментальные данные о всех входах и выходах черного ящика, то можно вычислить ошибку между экспериментальным и теоретическим значением Y для каждой i-ой точки и минимизировать суммарную ошибку F:
Для определения значений коэффициентов Am используется матричное уравнение Крамера с m+1 неизвестными:
Ошибка F зависит от выбора параметров А0, А1,…,Аm. По аналогии с одномерной моделью, для каждой точки вычисляется ошибка Ei затем находится суммарная ошибка F и значения и S и выполняется проверка гипотезы о линейности многомерного черного ящика.
14.Методы планирования эксперимента на модели. планирования эксперимента В планировании эксперимента различают входные (изогенные) и выходные (эндогенные) переменные:х1,х2,…,хк;y1,y2…,ym. Входные переменные в называют факторами а выходные — реакциями. Каждый фактор xi, i=1,2,…,k может принимать в эксперименте одно или несколько значений, называемых уровнями. Фиксированный набор уровней факторов определяет одно из возможных состояний рассматриваемой системы. Одновременно этот набор представляет собой условия проведения одного из возможных экспериментов. Каждому фиксированному набору уровню факторов соответствует определённая точка в многомерном пространстве, называемая факторным пространством. Эксперименты не могут быть реализованы во всех точках факторного пространства, а лишь в принадлежащих допустимой области, как это например оказано для случая двух факторов Х1 и Х2 на рисунке 9.1.
Рис.9.1. Факторное пространство План эксперимента обычно используется для определения экстремальной характеристики объекта. Поэтому планирование эксперимента называется экстремальным. Стратегическое планирование машинных экспериментов с моделями систем Можно выделить стратегическое и тактическое планирование эксперимента на моделях систем. Стратегическое планирование – ставит своей целью получение необходимой информации о системе с помощью модели, реализованной на ЭВМ. Тактическое планирование – определяет способы проведения каждой серии испытаний машинной модели.
17. Законы распределения случайной величины Дискретные законы распределения Пусть некоторая СВ является дискретной, т.е. может принимать лишь фиксированные значения Xi. В этом случае ряд значений вероятностей P(Xi) для всех (i=1…n) допустимых значений этой величины называют её законом распределения. Биномиальное распределение (распределение Бернулли) Возникает в тех случаях, когда ставится вопрос: сколько раз происходит некоторое событие в серии из определенного числа независимых наблюдений (опытов), выполняемых в одинаковых условиях.
P(X=
k) =
Формулу (1) называют формулой Бернулли. При большом числе испытаний биномиальное распределение стремиться к нормальному. Распределение Пуассона Всюду, где в течение определенного времени может происходить случайное число каких-то событий (радиоактивных распадов, телефонных вызовов, отказов оборудования, несчастный случаях и т.п.). Рассмотрим наиболее типичную ситуацию, в которой возникает распределение Пуассона. Пусть некоторые события (покупки в магазине) могут происходить в случайные моменты времени. Определим число появлений таких событий в промежутке времени от 0 до Т. Случайное число событий, происшедших за время от 0 до Т, распределено по закону Пуассона с параметром l=аТ, где а>0 – параметр задачи, отражающий среднюю частоту событий. Вероятность k покупок в течение большого интервала времени, (например, – дня) составит P(Z=k)
=
Непрерывные законы распределения Нормальное (гауссовское) распределение Нормальное (гауссовское) распределение занимает центральное место в теории и практике вероятностно-статистических исследований.Непрерывная случайная величина Х называется распределенной по нормальному закону, если ее плотность распределения равна
где
Равномерное распределение Равномерное распределение вероятностей является простейшим и может быть как дискретным, так и непрерывным. Дискретное равномерное распределение – это такое распределение, для которого вероятность каждого из значений СВ одна и та же, то есть:
где N – количество возможных значений СВ. Распределение вероятностей непрерывной CВ Х, принимающие все свои значения из отрезка [а;b] называется равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю:
20. Непараметрические проверки статистической гипотезы. Статистическая гипотеза – это предположение о свойствах случайных величин или событий, которое мы хотим проверить по имеющимся данным. Нулевая гипотеза – это основное проверяемое предположение, которое обычно формулируется как отсутствие различий, отсутствие влияние фактора, отсутствие эффекта, равенство нулю значений выборочных характеристик и т.п. Например: Имеется механическое устройство, выходное звено которого совершает вращательное движение. Гипотеза: увеличение скорости вращения выходного звена не влияет на устойчивость процессов внутри механизма. Другое проверяемое предположение (не всегда строго противоположное или обратное первому) называется конкурирующей или альтернативной гипотезой. Нулевая гипотеза обозначается Н0, а альтернативная как Н1. Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость проверить ее. Так как проверку производят статистическими методами, то данная проверка называется статистической. При проверке статистических гипотез возможны ошибки (ошибочные суждения) двух видов: H0=TRUE H1=FALSE можно отвергнуть нулевую гипотезу, когда она на самом деле верна (так называемая ошибка первого рода); H0=FALSE H1=TRUE можно принять нулевую гипотезу, когда она на самом деле не верна (так называемая ошибка второго рода). Непараметрический анализ выборок---Непараметрические критерии анализа выборок позволяют проводить анализ, не учитывая закон распределения. Такой анализ может быть проведен с помощью критерия знаков (G-критерий). Критерий предназначен для сравнения состояния некоторого свойства у членов двух зависимых выборок на основе измерений, сделанных по шкале не ниже ранговой. Имеется две серии наблюдений над случайными переменными X и У, полученные при рассмотрении двух зависимых выборок. На их основе составлено N пар вида (хi, уi), где хi, уi - результаты двукратного измерения одного и того же свойства у одного и того же объекта. Элементы каждой пары хi, уi сравниваются между собой по величине, и паре присваивается знак «+», если хi < уi , знак «-», если хi > уi и «0», если хi = уi. Нулевая гипотеза формулируются следующим образом: в состоянии изучаемого свойства нет значимых различий при первичном и вторичном измерениях. Альтернативная гипотеза: законы распределения величин X и У различны, т. е. состояния изучаемого свойства существенно различны в одной и той же совокупности при первичном и вторичном измерениях этого свойства. Нулевая гипотеза принимается на уровне значимости 0,05, если наблюдаемое значение T<n-ta, где значение n-ta определяется из статистических таблиц для критерия знаков.
22. Тактическое планирование эксперимента на модели.Планирование эксперимента В планировании эксперимента различают входные (изогенные) и выходные (эндогенные) переменные:х1,х2,…,хк;y1,y2…,ym. Входные переменные в называют факторами а выходные — реакциями. Каждый фактор xi, i=1,2,…,k может принимать в эксперименте одно или несколько значений, называемых уровнями. Фиксированный набор уровней факторов определяет одно из возможных состояний рассматриваемой системы. Одновременно этот набор представляет собой условия проведения одного из возможных экспериментов. Каждому фиксированному набору уровню факторов соответствует определённая точка в многомерном пространстве, называемая факторным пространством. Эксперименты не могут быть реализованы во всех точках факторного пространства, а лишь в принадлежащих допустимой области, как это например оказано для случая двух факторов Х1 и Х2 на рисунке 9.1.
Рис.9.1. Факторное пространство План эксперимента обычно используется для определения экстремальной характеристики объекта. Поэтому планирование эксперимента называется экстремальным.
Тактическое планирование – определяет способы проведения каждой серии испытаний машинной модели.
25. Дискретно – детерминированные модели (F- схемы) : Автомат Милли.
Конечный
автомат
представляет собой объект, который
функционирует в моменты автоматного
времени t0=0,
t1=T0,
t2=2T0
или в конечном виде
Принято различать два типа автоматов автомат Милля и автомат Мурра. Автомат Милли Формальное определение [обработка] Автомат Милля может быть задан в виде функционала:
Здесь:
Q
является множеством возможных
состояний
Множество
Σ является алфавитом ввода,
Множество
Ω является алфавитом выхода,
Переходная
функция имеет вид:
Функция
выхода определяется выражением:
В
конечном итоге выбирается компактная
нотация и обе функции сводятся к одной
переходной функции состояния
Множество
Автомат
Миля может быть представлен в виде
графа, дуга графа показывает переход
из одного состояния в другое. Обозначается
дуга кодом в виде
Пример автомата Милли
Переход
из одного состояния в другое показывается
дугами. Например, условное обозначение
дуги 0/1, означает, что при задании 0 для
смены состояний на выходе появляется
1.
27.Дискретно стохастические модели. (P- схемы):Вероятностный автомат Милли. Дискретно стохастические модели. (P- схемы)- Сущность дискретизации времени при дискретно – стохастическом подходе остается аналогичной конечным автоматом. Влияние стохастичности рассмотрим на разновидности этих автоматов, а именно на вероятностных автоматах. Вероятностный автомат – это дискретный преобразователь информации с памятью, функционирование которого, в каждом такте, зависит только от состояния памяти в нем и может быть описано стохастически. Рассмотрим
множество G,
элементами которого являются (xj,zs)
, xj
X – множество входных значений, Z – Множество возможных состояний. Если
существует две такие функции
Здесь Y – множество выходных значений. Введем
в рассмотрение более общую математическую
схему. Пусть Ф множество возможных
пар вида Ф(zk,yj);
yj Потребуем, чтобы любой элемент множества G порождал на множестве Ф некоторый закон распределения вида: Элементы из Ф …(z1 ,y1)… (z1 ,y2) …(zk ,yj-1) (zk ,yJ) (xi,zs) ….b11… b12…bk(j-1) bkJ
Число таких распределений равно числу элементов множества G и составляют множество B . Тогда кортеж P=<Z,X,Y,B> называется вероятностным автоматом. Вероятностный автомат Милли--Пусть элементы множества G порождает некоторые законы распределения на множествах Z и Y. Элементы из Y y1 ,y2 ….., yj-1 ,yj (xi,zs) q1 ,q2 ….., qj-1 ,qj Элементы из Z z1 , z2 ….., zk-1 , zk (xi,zs)
Если для всех k и j выполняется условие qkzi=bkj, то такой P- автомат называется вероятностным автоматом Милли. У такого автомата распределения независимы для нового состояния и его выходного сигнала.
28.Дискретно стохастические модели. (P- схемы):Вероятностный автомат Мура. Дискретно стохастические модели. (P- схемы) Сущность дискретизации времени при дискретно – стохастическом подходе остается аналогичной конечным автоматом. Влияние стохастичности рассмотрим на разновидности этих автоматов, а именно на вероятностных автоматах. Вероятностный автомат – это дискретный преобразователь информации с памятью, функционирование которого, в каждом такте, зависит только от состояния памяти в нем и может быть описано стохастически.
Рассмотрим
множество G,
элементами которого являются (xj,zs)
, xj
X – множество входных значений, Z – Множество возможных состояний.
Если
существует две такие функции
Здесь Y – множество выходных значений.
Введем
в рассмотрение более общую математическую
схему. Пусть Ф множество возможных
пар вида Ф(zk,yj);
yj Потребуем, чтобы любой элемент множества G порождал на множестве Ф некоторый закон распределения вида: Элементы из Ф …(z1 ,y1)… (z1 ,y2) …(zk ,yj-1) (zk ,yJ) (xi,zs) ….b11… b12…bk(j-1) bkJ
Число таких распределений равно числу элементов множества G и составляют множество B . Тогда кортеж P=<Z,X,Y,B> называется вероятностным автоматом. Вероятностный автомат Мура---Пусть определение выходного сигнала P–автомата завит лишь от того состояния, в котором находится автомат в данном такте работы. Элементы из Y y1 ,y2 ….., yi-1 ,yi zk s1 ,s2 ......., si-1 ,si
si
– вероятность выдачи выходного сигнала
yi
при условии ,что автомат находится zk Если для всех k и i выполняется условие zksi=bki, то такой P- автомат называется вероятностным автоматом Мура. Y и Z детерминированные автоматы-- Частным случаем Р-автомата, задаваемого как P=<Z,X,Y,B> являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминировано. Если выходной сигнал Р-автомата определяется детерминировано, то такой автомат называется Y-детерминированным вероятностным автоматом. Аналогично, Z- детерминированным вероятностным автоматом называется Р-автомат, у которого выбор нового состояния является детерминированным.
32.Дискретно – событийные модели. Системы называются дискретно-событийными (или просто дискретными), если изменения переменных состояния в них происходят только в явно определенные моменты времени или под влиянием явно определенных событий. Находясь в некотором состоянии, дискретная система сохраняет его (не изменяет своих характеристик) до наступления очередного события, под воздействием которого переменные системы (и, следовательно, ее состояние) изменяются скачком. Для создания моделей такого типа в программе AnyLogic ver 6.4 используется механизм событий.
В случае использования режима a нужно задать период срабатывания в единицах модельного времени. При использовании первого события с режимом b нужно указать Время первого срабатывания Период срабатывания (число единиц модельного времени) При выборе режима с событие должно управляться вызовом специального метода restart( double t), где t – период срабатывания события. Событие, происходящее с заданной интенсивностью, используется для моделирования потока независимых событий (пуассоновский поток). Такое событие выполняется периодически с интервалами времени, подчиняющимися экспоненциальному закону распределения с параметром, равным заданной интенсивности. Например, если интенсивность равна 5, то событие будет происходить в среднем 5 раз в единицу модельного времени. Третий тип события выполняется один раз при выполнении определенного условия, чтобы продолжить проверку выполнения условия и следовательно повторить выполнение события нужно вызвать его метод restart().
34. Классификация систем массового обслуживания. Теория систем массового обслуживания используется для описания сервисных систем с помощью элементарной модели. Это модель состоит из так называемого селектора обслуживания, который располагает одной или более машиной одинакового типа или рабочим местом. Клиенты системы обращаются к ней поодиночке и в случайные моменты времени обращаясь к прибору обслуживания. Вновь прибывший клиент обслуживается только в том случае, если хотя бы один из приборов обслуживания свободен, в противном случае он должен быть поставлен в очередь ожидания.
- поток пребывающих клиентов - коэффициент интенсивности обслуживания с-число обслуживающих узлов Понятие клиент и переключатель на практике могут иметь различное значение, например автомобили перед сфетофором, компьютерные программы, которые циркулируют в вычислительной системе, телефонные вызовы которые поступают на телефонный узел и т.д. Базовая модель может быть представлена различными способами. Клиенты обслуживаются не по одиночке, а группами. Применение: безотходное производство продукции Некоторые клиенты покидают систему, прежде чем они были обслужены (СМО с ограничением времени) Пример: Хранение скоропортящихся продуктов Не все приборы обслуживания предоставляются клиентам(СМО с ограниченным доступом) Применение: Конвейеры с определенным набором оборудования, определенный набор оборудования в телефонной сети. Некоторые клиенты отказываются обращать в СМО, так как очередь ожидания для них слишком длинная. Пример: обычное поведения в точках обслуживания на почте, банке, кассах продажи билетов. Клиент с высоким приоритетом вытесняет клиента с низшим приоритетом из процесса обслуживания (СМО с приоритетным управлением) Пример: оперативное управления производством в целях снижения затрат и получения высокой прибыли Клиент, которой при своем прибытии не сразу обслуживается, вытесняется из системы (Системы с потерями) Пример телефонные вызовы в междугордних сетях Поток поступающих заявок описывается через посредством так называемого процесса обновления заявок. При этом предполагается, что все заявки в порядке их поступления подлежат сквозной нумерации. Интервал времени In между прибытием (n-1) и n ного клиента, обозначается как время прибытия между двумя заявками. О случайных переменных In,n=1,2,.. можно сделать следующие предположение, что они стохастически независимы и обладают одинаковым законом распределения с функцией распределения FI(x), значением вероятности E[I] и дисперсией D[i] Значение
Называется интенсивностью прибытия заявок и показывает, сколько клиентов в среднем в единицу времени поступает в систему. Интервал времени на обслуживание Sn,n=1,2,…клиентов следующих друг за другом, также стохастически независимы и характеризуются случайными переменными с идентичным законом распределения. Функция распределения интервалов обслуживания обозначается как FS(x). Для обозначения вероятности и дисперсии вводятся условные обозначения E[S] и D[S] соответственно.
Величина называется интенсивностью процесса обслуживания, она показывает сколько клиентов в среднем в единицу может быть обслужено в системе. Если в системе существует несколько параллельных и одинаковых приборов обслуживания, эта величина повышается в соответствии с числом приборов. Привило обслуживания жестко определяет в какой последовательности будут обслужены клиенты системы. Существуют следующие правила обслуживания: FIFO(FCFS) First In, First Out(First Come,First Served) Обслуживание выполняется в порядке поступления заявок LIFO(LCFS) Last In, First Out(Last Come,First Served) Обслуживание выполняется в обратно порядке прибытия заявок SIRO Selection in Random Order. Следующий клиент выбирается случайным образом Non-preemptive priority Относительный приоритет, некоторым клиентам отдается предпочтение по отношению к другим клиентам. Текущий процесс обслуживания не прерывается Preemptive priority. Абсолютный приоритет. Если вновь прибывший клиент обладает высшим приоритетом по сравнению с другими клиентами в системе, текущий процесс обслуживания прерывается и продолжается с новыми условиями. Прежние условия-требования отклоняются. RR (Round Robin) Каждый клиент может занять обслуживающий процесс на определенный временной интервал. Клиенты, чье обслуживание требует больше времени, должны несколько раза ставится в очередь на обслуживание. Для символического обозначения СМО используется нотация Кендала , Гнеденко A/B/c/m Символы A и B обозначают тип распределения интервалов времени прибытия заявок и времени обслуживания. Символ c используется для обозначения числа параллельных приборов обслуживания, а символ m обозначает мощность очереди. Примеры условных обозначений распределений M- експоненциальное распределение Ek- распределение Эрланга (k=1,2,…) G-нормальное распределение
40. Модель отказов системы массового обслуживания. Анализ надёжности сложных систем и оптимизация их обслуживания Обеспечение надёжности сложных систем является важной практической задачей. Особенность задачи состоит в том, что заявки в систему (это отказы машин или устройств) поступают не извне, а возникают в самой системе и не выходят из нее после обслуживания (замкнутая система). При этом поток заявок (неисправностей) будет максимальным, когда все машины исправны, и уменьшается по мере выхода из строя последующих машин (максимальное количество отказов будет соответствовать общему парку машин, которое обозначим М). Восстановление машин обеспечивают мастера ремонтных бригад количество бригад обозначим N). Граф состояний такой системы для N>2 показан на рис. 4.4.
На представленной схеме индекс у состояния Ск соответствует количеству отказавших машин. Эта схема соответствует типу "размножена и гибели", её уравнения подобны (4.7) и описывают стационарный процесс, который стремится к установившемуся решению.
Обозначим
поток отказов одной машины
Установившийся режим для стационарного марковского процесса после введения этих параметров будет описываться системой линейных алгебраических уравнений.
|








 Рис.9.4
Объект с несколькими входами и
возмущением
Рис.9.4
Объект с несколькими входами и
возмущением =
=
 - х1) + (
- х1) + ( - х2) + ... + (
- х2) + ... + ( - хn) =0
- хn) =0

 — выборочное среднее, N — число
наблюдений в выборке.
— выборочное среднее, N — число
наблюдений в выборке.
 )2+p2(x2-
)2+p2(x2- )2+…+pn(xn-
)2+…+pn(xn- )2
)2

 .Здесь
T0
период дискретизации модели автомата.
В каждый момент ti
.Здесь
T0
период дискретизации модели автомата.
В каждый момент ti
 T,
автомат может находиться в одном из
конечного числа состояний zj
T,
автомат может находиться в одном из
конечного числа состояний zj Z.
Z.
 .
Здесь Q конечное множество состояний
.
Здесь Q конечное множество состояний
 ,
множество
- входной алфавит автомата
,
множество
- входной алфавит автомата
 ,
множество
- выходной алфавит автомата
,
множество
- выходной алфавит автомата
 .Переходная
функция автомата описывается выражением
.Переходная
функция автомата описывается выражением
 ,
а функция выхода имеет вид
,
а функция выхода имеет вид

 находится
в состоянии из множества F,
тогда слово J
принадлежит словарю языка автомата
L(A).
находится
в состоянии из множества F,
тогда слово J
принадлежит словарю языка автомата
L(A).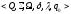 .
Известны следующие значения для
множеств автомата
.
Известны следующие значения для
множеств автомата



 количество
заявок, которое одновременно может
находиться в накопителе. L
– емкость i-го
накопителя и канала обслуживания
заявок Ki.
количество
заявок, которое одновременно может
находиться в накопителе. L
– емкость i-го
накопителя и канала обслуживания
заявок Ki.
 вероятность ожидания обслуживания и
вероятность ожидания обслуживания и

 ,
и
,
и
 ,
коэффициенты вариации интервалов
времени между прибытиями заявок и
временами на обслуживание. Формула
позволяет сделать вывод, что число
клиентов в системе чем больше система
загружена и чем больше вариативные
коэффициенты. Для того чтобы получить
ограниченную очередь ожидания нужно
иметь систему высокой производительности
или ограничить вариативность системы.
,
коэффициенты вариации интервалов
времени между прибытиями заявок и
временами на обслуживание. Формула
позволяет сделать вывод, что число
клиентов в системе чем больше система
загружена и чем больше вариативные
коэффициенты. Для того чтобы получить
ограниченную очередь ожидания нужно
иметь систему высокой производительности
или ограничить вариативность системы. .
При
постоянных интервалах поток называют
регулярным.
.
При
постоянных интервалах поток называют
регулярным.
 Отсюда
можно по функции экспоненциального
распределения определить вероятность
безотказной работы прибора в течение
времени Т:P(T)=e-T
Отсюда
можно по функции экспоненциального
распределения определить вероятность
безотказной работы прибора в течение
времени Т:P(T)=e-T
 при t->0
при
при t->0
при Рис.1.1.
Структура класса.
Рис.1.1.
Структура класса. Рис.1.3.
Класс A
зависит от класса B.
Рис.1.3.
Класс A
зависит от класса B. Рис.
1.4. Связь с ролями.
Рис.
1.4. Связь с ролями. Рис.1.5.
Связь один ко многим.
Рис.1.5.
Связь один ко многим. Рис.
1.8. Наследование. Класс A является
суперклассом для класса B.
Рис.
1.8. Наследование. Класс A является
суперклассом для класса B.
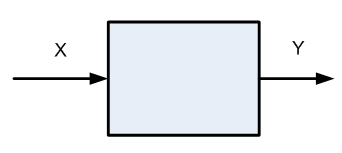




 и
и
 попадает более 70% экспериментальных
точек, то выдвинутая гипотеза
принимается.
попадает более 70% экспериментальных
точек, то выдвинутая гипотеза
принимается. и
и
 .
.



 ,
,
 — средние арифметические в
экспериментальной и контрольной
группах,
— средние арифметические в
экспериментальной и контрольной
группах, -
стандартная ошибка разности средних
арифметических. Находится из формулы:
-
стандартная ошибка разности средних
арифметических. Находится из формулы: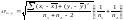


 среднее значение разностей
среднее значение разностей
 двух выборок X и Y.
двух выборок X и Y.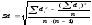

 дисперсии первой и второй выборки
соответственно.
дисперсии первой и второй выборки
соответственно.
 (1)
(1)


 (2) – уравнение в
нормальной форме Коши
(2) – уравнение в
нормальной форме Коши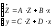 (3) – уравнение в
пространстве состояний
(3) – уравнение в
пространстве состояний ;
;
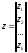 - вектор – столбец
переменных или координат состояний.
- вектор – столбец
переменных или координат состояний.
 .
.

 Матрица
А определяется выражением (4)
Матрица
А определяется выражением (4)




 ,
называется пространством состояний.
Размерность пространства равна порядку
системы дифференциальных уравнений.
Если в уравнении (3) перейти от функции
времени, т.е. векторов
,
называется пространством состояний.
Размерность пространства равна порядку
системы дифференциальных уравнений.
Если в уравнении (3) перейти от функции
времени, т.е. векторов
 к
их преобразованию по Лапласу, предполагая
начальные условия нулевыми, т.е.
к
их преобразованию по Лапласу, предполагая
начальные условия нулевыми, т.е.
 ,
то:
,
то:


 на выражение :
на выражение :




 1=z2;
1=z2; 2=z3;
2=z3; 3=
-a3z1-a2·z2-a1·z3+b0u
3=
-a3z1-a2·z2-a1·z3+b0u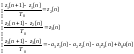
 Где
n=1, 2, 3,…
Где
n=1, 2, 3,…
 ,
агрегата A0
и оператора R
считают А-схемой при следующих
ограничениях:
,
агрегата A0
и оператора R
считают А-схемой при следующих
ограничениях:








 Рис.8.2
Экспериментальные точки
Рис.8.2
Экспериментальные точки






 .Здесь
T0
период дискретизации модели автомата.
В каждый момент ti
.Здесь
T0
период дискретизации модели автомата.
В каждый момент ti
 T,
автомат может находиться в одном из
конечного числа состояний zj
T,
автомат может находиться в одном из
конечного числа состояний zj Z.
Z.

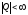 .
Вместо Q часто используется также
условное обозначение в виде латинской
буквы Z.
.
Вместо Q часто используется также
условное обозначение в виде латинской
буквы Z. .
. .
. .
.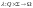 .
. .
. Это
стартовое-начальное состояние. Вместо
q0
могут быть использованы условные
обозначения начального состояния z0
и s0.
Такое начальное состояние может быть
отмечено двойной стрелкой.
Это
стартовое-начальное состояние. Вместо
q0
могут быть использованы условные
обозначения начального состояния z0
и s0.
Такое начальное состояние может быть
отмечено двойной стрелкой. это конечное множество возможных
доступных состояний. Когда автомат
после чтения входных слов
это конечное множество возможных
доступных состояний. Когда автомат
после чтения входных слов
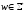 находится в состоянии из множества
F, то слово w относится к словарному
множеству автомата L(A). Множество F
может не использоваться, в этом случае
находится в состоянии из множества
F, то слово w относится к словарному
множеству автомата L(A). Множество F
может не использоваться, в этом случае
 является частью словаря автомата, и
оно определяется выходом автомата.
является частью словаря автомата, и
оно определяется выходом автомата. ,
то есть переход происходит в зависимости
от значения из множества алфавита
ввода и значения из множества алфавита
вывода. Пример автомата Милли показан
на рисунке. Начальное состояние
автомата отмечено как q0.
,
то есть переход происходит в зависимости
от значения из множества алфавита
ввода и значения из множества алфавита
вывода. Пример автомата Милли показан
на рисунке. Начальное состояние
автомата отмечено как q0.

 X,
zs
X,
zs
 Z
Z ,
f
с помощью которых выполняется
отображение G
,
f
с помощью которых выполняется
отображение G Z,
G
Z,
G Y,
то говорят что пятерка элементов,
входящая в кортеж F=(Z,X,Y,
Y,
то говорят что пятерка элементов,
входящая в кортеж F=(Z,X,Y, ,f)
определяет автомат детерминированного
типа.
,f)
определяет автомат детерминированного
типа. Y
Y ;
bkj
– это вероятность перехода автомата
в состояние zk
и выдачи выходного сигнала yj
,
если автомат находиться в состоянии
zs
и на его вход поступил входной сигнал
xi
;
bkj
– это вероятность перехода автомата
в состояние zk
и выдачи выходного сигнала yj
,
если автомат находиться в состоянии
zs
и на его вход поступил входной сигнал
xi 1
,
1
,
 2
…..,
2
…..,
 k-1,
k-1, k
k qj
и
qj
и k,это
вероятности перехода автоматов в
состояние zk
и появления выходного сигнала yk
,
если автомат находиться в состоянии
zs
и на его вход поступил входной сигнал
xi.
k,это
вероятности перехода автоматов в
состояние zk
и появления выходного сигнала yk
,
если автомат находиться в состоянии
zs
и на его вход поступил входной сигнал
xi.
 X,
zs
X,
zs
 Z
Z ,
f
с помощью которых выполняется
отображение G
,
f
с помощью которых выполняется
отображение G Z,
G
Z,
G Y,
то говорят что пятерка элементов,
входящая в кортеж F=(Z,X,Y,
Y,
то говорят что пятерка элементов,
входящая в кортеж F=(Z,X,Y, ,f)
определяет автомат детерминированного
типа.
,f)
определяет автомат детерминированного
типа. Y
Y ;
bkj
– это вероятность перехода автомата
в состояние zk
и выдачи выходного сигнала yj
,
если автомат находиться в состоянии
zs
и на его вход поступил входной сигнал
xi
;
bkj
– это вероятность перехода автомата
в состояние zk
и выдачи выходного сигнала yj
,
если автомат находиться в состоянии
zs
и на его вход поступил входной сигнал
xi


 ,
где
z
- средний
период
безотказной
работы одной машины. Если среднее
время ремонта одной
машины
равно w,
то
производительность восстановления
будет
,
где
z
- средний
период
безотказной
работы одной машины. Если среднее
время ремонта одной
машины
равно w,
то
производительность восстановления
будет
 .
.