Регрессионные модели ------Линейные регрессионные модели

В целях исследований часто бывает удобно представить исследуемый объект в виде ящика, имеющего входы и выходы, не рассматривая детально ею внутренней структуры.

По степени информированности исследователя об объекте существует деление объектов на три типа «ящиков»:

• «белый ящик»: об объекте известно все;

• «серый ящик»: известна структура объекта, неизвестны количественные значения параметров;

• «черный ящик»: об объекте неизвестно ничего.

Черный ящик условно изображают как на рисунке 8.1.

Рис.8.1. Модель черного ящика

Значения на входах и выходах черного ящика можно наблюдать и измерять. Содержимое ящика неизвестно.

Задача состоит в том, чтобы, зная множество значений на входах и выходах, построить модель, то есть определить функцию ящика, по которой вход преобразуется в выход. Такая задача называется задачей регрессионного анализа.

В зависимости от того, доступны входы исследователю для управления или только для наблюдения, можно говорить про активный или пассивный эксперимент с ящиком.

Результаты наблюдений за объектом имеют вид, показанный на рисунке 8.2. Всего на графике n экспериментальных точек.

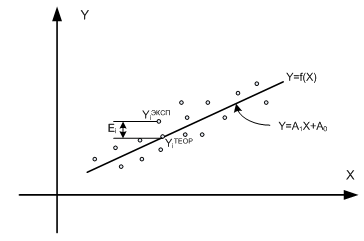Рис.8.2 Экспериментальные точки

Предположим, что мы имеем дело с черным ящиком, имеющим один вход и один выход. Допустим, что зависимость между входом и выходом линейная или близка к линейной. Тогда данная модель будет называться линейной одномерной регрессионной моделью.

Для проверки сделанного допущения нужно выполнить последовательность действий, которая изложена ниже.

1) Исследователь вносит гипотезу о структуре ящика.

Рассматривая экспериментально полученные данные, предположим, что они подчиняются линейной гипотезе, то есть выход Y зависит от входа X линейно, и гипотеза имеет вид:

y=A₁X+A₀

2) Определение неизвестных коэффициентов A₀ и A₁ модели

Линейная одномерная модель модель черного ящика показана на рисунке 8.3.

Рис. 8.3. Гипотеза. Черный ящик с одним входом и выходом

Ошибки E_i, для всех n точек наблюдений следует сложить. Чтобы положительные ошибки не компенсировали в сумме отрицательные, каждую из ошибок возводят в квадрат и складывают их значения в суммарную ошибку F уже одного знака:

Цель метода — минимизация суммарной ошибки F за счет подбора коэффициентов A₀, A₁.

Необходимо найти такие коэффициенты A₀, A₁ линейной функции Y=A₁X+A₀, чтобы ее график проходил как можно ближе одновременно ко всем экспериментальным точкам. Поэтому данный метод называется методом наименьших квадратов.

Суммарная ошибка F является функцией двух переменных A₀ и А₁, то есть F(A₀,A₁), меняя которые, можно влиять на величину суммарной ошибки .

Для нахождения коэффициентов A0, A1 используют матричное уравнение Крамера:

3) Проверка гипотезы. Проверка гипотезы выполняется путем расчета ошибки по формулам

Рис.8.4. Проверка гипотезы

Если в полосу, ограниченную линиями ипопадает более 70% экспериментальных точек, то выдвинутая гипотеза принимается.

Допускается повышение критерия надежности гипотезы. В этом случае используют контрольную полосу, ограниченную линиями и.

Расстояние S связано с  следующим соотношением:

Рассмотренная проверка гипотезы основывается на предположении о нормальном законе распределения случайных ошибок.

12. . Многомерная модель черного ящика и линейная регрессия.