Вероятностный автомат Милли--Пусть элементы множества g порождает некоторые законы распределения на множествах z и y.

Элементы из Y y₁ ,y₂ ….., y_j-1 ,y_j

(x_i,z_s) q₁ ,q₂ ….., q_j-1 ,q_j

Элементы из Z z₁ , z₂ ….., z_k-1 , z_k

(x_i,z_s) ₁ , ₂ ….., _k-1,_k

q_j и_k,это вероятности перехода автоматов в состояние z_k и появления выходного сигнала y_k , если автомат находиться в состоянии z_s и на его вход поступил входной сигнал x_i.

Если для всех k и j выполняется условие q_kz_i=b_kj, то такой P- автомат называется вероятностным автоматом Милли. У такого автомата распределения независимы для нового состояния и его выходного сигнала.

25. Дискретно стохастические модели. (P- схемы):Вероятностный автомат Мура.

Дискретно стохастические модели. (p- схемы)

Сущность дискретизации времени при дискретно – стохастическом подходе остается аналогичной конечным автоматом. Влияние стохастичности рассмотрим на разновидности этих автоматов, а именно на вероятностных автоматах.

Вероятностный автомат – это дискретный преобразователь информации с памятью, функционирование которого, в каждом такте, зависит только от состояния памяти в нем и может быть описано стохастически.

Рассмотрим множество G, элементами которого являются (x_j,z_s) , x_j X, z_s Z

X – множество входных значений, Z – Множество возможных состояний.

Если существует две такие функции , f с помощью которых выполняется отображение GZ, G Y, то говорят что пятерка элементов, входящая в кортеж F=(Z,X,Y,,f) определяет автомат детерминированного типа.

Здесь Y – множество выходных значений.

Введем в рассмотрение более общую математическую схему. Пусть Ф множество возможных пар вида Ф(z_k,y_j); y_jY

Потребуем, чтобы любой элемент множества G порождал на множестве Ф некоторый закон распределения вида:

Элементы из Ф …(z₁ ,y₁)… (z₁ ,y₂) …(z_k ,y_j-1) (z_k ,y_J)

(x_i,z_s) ….b₁₁… b₁₂…b_k(j-1) b_kJ

; b_kj – это вероятность перехода автомата в состояние z_k и выдачи выходного сигнала y_j , если автомат находиться в состоянии z_s и на его вход поступил входной сигнал x_i

Число таких распределений равно числу элементов множества G и составляют множество B . Тогда кортеж P=<Z,X,Y,B> называется вероятностным автоматом.

Вероятностный автомат Мура---Пусть определение выходного сигнала p–автомата завит лишь от того состояния, в котором находится автомат в данном такте работы.

Элементы из Y y₁ ,y₂ ….., y_i-1 ,y_i

z_k s₁ ,s₂ ......., s_i-1 ,s_i

s_i – вероятность выдачи выходного сигнала y_i при условии ,что автомат находится z_k

Если для всех k и i выполняется условие z_ks_i=b_ki, то такой P- автомат называется вероятностным автоматом Мура.

Y и Z детерминированные автоматы-- Частным случаем Р-автомата, задаваемого как P=<Z,X,Y,B> являются автоматы, у которых либо переход в новое состояние, либо выходной сигнал определяются детерминировано. Если выходной сигнал Р-автомата определяется детерминировано, то такой автомат называется Y-детерминированным вероятностным автоматом. Аналогично, Z- детерминированным вероятностным автоматом называется Р-автомат, у которого выбор нового состояния является детерминированным.

25. Непрерывно-стохастические модели (Q-схемы).

Непрерывно-стохастические модели (q-схемы) Основные понятия и определения

Система массового обслуживания представляет собой класс математических схем, разработанных в теории массового обслуживания и приложений для формализации процессов функционирования систем, которые, по своей сути, являются процессами обслуживания. Характерным для таких объектов является случайное появление требований (заявок) на обслуживание и завершение обслуживания в случайные моменты времени.

В любом элементарном акте обслуживания можно выделить две составляющие:

1. ожидание обслуживания

2. обслуживание заявки

Процесс обслуживания можно представить в виде прибора обслуживания Пi.

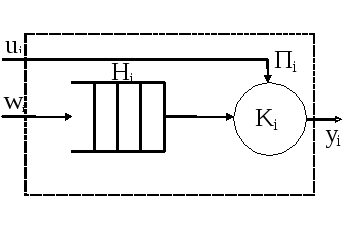
Нi – накопитель

ui- поток обслужмвания

wi- поток заявок

Ki – канал обслуживания заявки.

количество заявок, которое одновременно может находиться в накопителе. L – емкость i-го накопителя и канала обслуживания заявок Ki.

При моделировании реальных систем используют композиции из отдельных элементарных систем, которые называют Q-схемами. Если каналы отдельных приборов соединены параллельно, то имеет место многоканальное обслуживание, т.е. многоканальная Q-схема. Если приборы и их параллельные композиции соединены последовательно, то имеет место многофазное обслуживание, т.е. многофазная Q-схема.

Для задания Q-схемы необходимо определить оператор сопряжения он отражает взаимосвязь элементов структуры, т.е. каналов и накопителей между собой.

Различают разомкнутые и замкнутые Q-схемы. В разомкнутых Q-схемах обратные связи отсутствуют. В замкнутых Q-схемах есть обратные Q-связи, по которым заявки двигаются в направлении, обратном направлению «вход-выход».

25. Сети Петри - N схемы.Сети Петри. N схемы

В практике моделирования объектов часто приходится решать

задачи, связанные с формализованным описанием и анализом причинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов.

Формальное описание структур таких систем, взаимодействие параллельных систем и процессов может быть получено с помощью сетей Петри ( К. Петри).

Сеть Петри представляет собой двухдольный направленный граф. Такой граф состоит из следующих элементов:

позиций

переходов.

Позиции и переходы соединяются между собой направленными дугами. В графе Петри не существует прямых соединений между двумя позициями или двумя переходами.

Позиции обозначаются окружностями, переходы показываются в виде прямоугольников. Позиция обладает определенной мощностью и в соответствии с мощностью может содержать несколько знаков (маркеров). Если значение мощности не задано, то оно принимается равной бесконечности или единице. Каждой дуге графа может быть поставлен в соответствие определенный «вес». Если это значение не указано, то принимается значение равное единице.

Загрузка позиций маркерами, называется маркировкой и представляет собой состояние сети.

Переход считается активным или готовым к активации если во всех входных позициях находится такое число маркеров, которое соответствует весу перехода и все выходные позиции обладают достаточной мощностью – емкостью для того чтобы принять новые маркеры.

Переходы готовые к активизации могут, активированы в произвольный момент времени. При включении перехода из входных его входных позиций выбираются маркеры в соответствии с весом дуги и помещаются в выходные позиции в соответствии с весами дуг.

Пример работы сети Петри

Дано сеть. В каждой позиции может находится два маркера.

Схема переходов показана в таблице.

Разметка	Активный переход
M0={0,0}	-
M1={1,0}	d1
M2={2,0}	d1
M3={1,1}	d2
M4={0,2}	d2
M5={0,1}	d3
M6={0,0}	d3

Рис.. Маркировки M0 и M1.

Рис.. Маркировки M2 и M3

Рис. Маркировки M4 и M5.

После срабатывания перехода d3 на второй схеме маркировка становится равно M6=M0.

25. Обобщенные модели (А - схемы).