Классификация экспериментов

Различные виды экспериментов схематично представлены на рисунке 9.2.

Рис. 9.2. Объект с одним входом и выходом

Однофакторный пассивный эксперимент проводится путем выполнения n пар измерений в дискретные моменты времени единственного входного параметра X и соответствующих значений выходного параметра Y  (см. рисунок 9.2). Аналитическая зависимость между этими параметрами вследствие случайного характера возмущающих воздействий рассматривается в виде зависимости математического ожидания Y от значения X, носящей название регрессионной. Целью однофакторного пассивного эксперимента является построение регрессионной модели - установление зависимости y=f(x).

Рис. 9.3. Объект с несколькими входами

Многофакторный пассивный эксперимент проводится при контроле значений нескольких входных параметров X_i  (см. рисунок 9.3) и его целью является установление зависимости выходного параметра от двух или более переменных y=F(x₁,x₂,…) .

Рис. 9.4. Объект с несколькими входами и возмущением

Полный факторный эксперимент предполагает возможность управлять объектом по одному или нескольким независимым каналам (см. рисунок 9.4).

            В общем случае, схема эксперимента может быть представлена в виде, представленном на рисунке 9.4. В схеме используются следующие группы параметров:

• управляющие (входные x_i)

• параметры состояния (выходные Y)

• возмущающие воздействия (W_i)

При многофакторном и полном факторном эксперименте выходных параметров может быть несколько.

            Управляющие параметры x_i  представляют собой независимые переменные, которые можно изменять для управления выходными параметрами. Если i=1 (один управляющий параметр), то эксперимент однофакторный. Многофакторный эксперимент соответствует конечному числу управляющих параметров. Полный факторный эксперимент соответствует наличию возмущающих воздействий в многофакторном эксперименте.

Диапазон изменения факторов x_i  или число значений, которое они могут принимать называется уровнем фактора.

 Полный факторный эксперимент характеризуется тем, что при фиксированных возмущающих воздействиях W_i  минимальное число уровней каждого фактора равно двум. В этом случае, зафиксировав все факторы x_i  кроме одного, необходимо провести два измерения, соответствующих двум уровням этого фактора. Последовательно осуществляя такую процедуру для каждого из факторов x_i, получим необходимое число N опытов в полном факторном эксперименте для реализации всех возможных сочетаний уровней факторов N=2^k , где k - число факторов.

16. Матрица планирования эксперимента.

Приведем пример планирования эксперимента. Пусть необходимо взвесить на весах три тела разной массы A,B,C при условии, что нулевое положение весов не отрегулировано. При составлении плана эксперимента принято строить матрицу планирования. В таблице 9.1 приведен первый план взвешивания. «1» и «-1» соответствуют наличию или отсутствию объекта на весах.

Таблица 9.1.

План взвешивания, вариант №1

№ опыта	A	B	C	Результаты взвешивания
1	-1	-1	-1	y0
2	+1	-1	-1	y1
3	-1	+1	-1	y2
4	-1	-1	+1	y3

 Эксперимент состоит из четырех опытов. При первом опыте снимаются показания пустых весов, и выставляется их нулевое положение, затем отдельно взвешивается каждый из объектов. Расчет веса и погрешности измерений ² каждого из тел производится по следующим формулам:

 

Поскольку погрешности независимых измерений складываются, а вес каждого объекта получен в результате двух измерений, погрешность составляет 2².

Оптимально будет провести эксперимент по схеме, показанной в Таблице 9.2. В этом случае взвешивается отдельно каждый из объектов и все объекты вместе.  Непосредственное измерение погрешности y₀ не проводят.

Таблица 9.2

План взвешивания, вариант №2

№ опыта	A	B	C	Результаты взвешивания
1	+1	-1	-1	y1
2	-1	+1	-1	y2
3	-1	-1	+1	y3
4	+1	+1	+1	y4

 В этом случае выигрыш при проведении эксперимента заключается в том, что масса каждого из объектов вычисляется по новым формулам, а дисперсия результатов оказывается вдвое меньше. Этот результат получается за счет того, что при втором плане эксперимента смещение нуля измерительной аппаратуры (весов) исключено.

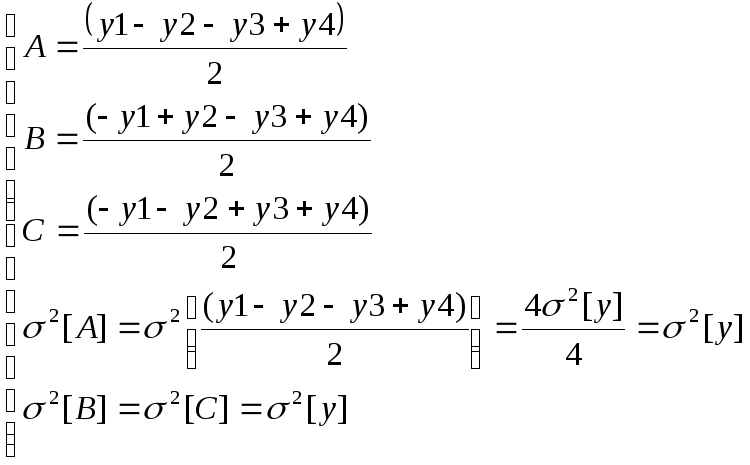
Планирование эксперимента позволяет либо уменьшить число измерений, либо увеличить их точность.

17. Законы распределения случайной величины.

СВ – это численная характеристика, измеряемая по ходу опыта и зависящая от случайного исхода. СВ реализуемая по ходу опыта и сама является случайной. Каждая СВ задает распределение вероятностей.

Основным свойством процессов, явлений в системах является их вероятностный характер (при данных условиях они могут произойти, реализоваться, но могут и не произойти). Для таких явлений существенную роль играет понятие вероятности.

Вероятность (Р) показывает степень возможности осуществления данного события, явления, результата. Вероятность невозможного события равна нулю, достоверного — единице (100%). Вероятность любого события лежит в пределах от 0 до 1 - в зависимости от того, насколько это событие случайно.

Если мы интересуемся событием A, то, скорее всего, можем наблюдать, фиксировать факты его появления. Потребность в понятии вероятности и ее вычисления возникнет, очевидно, только тогда, когда мы наблюдаем это событие не каждый раз, либо осознаем, что оно может произойти, а может не произойти. И в том и другом случае полезно использовать понятие частоты появления события f(A) - как отношения числа случаев его появления (благоприятных исходов) к общему числу наблюдений. Частота наступления случайного события зависит не только от степени случайности самого события, но и от числа (количества) наблюдений за этой СВ.

Существует два вида выборок СВ: зависимые и независимые. Если результаты измерения некоторого свойства у объектов первой выборки не оказывают влияния на результаты измерения этого свойства у объектов второй выборки, то такие выборки считаются независимыми. В тех случаях, когда результаты одной выборки влияют на результаты другой выборки, выборки считают зависимыми. Классический способ получения зависимых измерений – это двукратное измерение одного и того же свойства (или разных свойств) у одной и той же системы.

Событие А не зависит от события В, если вероятность события А не зависит от того произошло или нет событие В. События А и В независимы, если Р(АВ)=Р(А)Р(В). На практике независимость события устанавливается из условий опыта, интуиции исследователя и практики.

СВ бывает дискретной (мы можем пронумеровать ее возможные значения), например, выпадение игральной кости =4,6,2,1,5,3  и непрерывной (ее функция распределения F(x) – непрерывна), например, время службы лампочки.

Математическое ожидание – числовая характеристика СВ, приближенно равная среднему значению СВ:

M(x)=x₁p₁+x₂p₂+…+x_np_n

Дисперсия случайной величины

D(x)=p₁(x₁-)²+p₂(x₂-)²+…+p_n(x_n-)²