пособия по химии / лекции по ТД / Кинетика_лекции / лекция 2

Лекция по теме «Зависимость скорости химической реакции

от температуры»

Учебные вопросы

1. Уравнение Аррениуса

2. Энергия активации

3. Распределение молекул по энергиям

4. Энтропия активации. Стерический фактор

5. Решение уравнения Аррениуса

1. Уравнение Аррениуса

В большинстве случаев, скорость химической реакции увеличивается при повышении температуры. При этом возрастает константа скорости реакции.

Зависимость константы скорости реакции от температуры выражается уравнением Аррениуса:

,

(1)

где k - константа скорости реакции;

A - константа, называемая предэкспоненциальным множителем;

- основание натурального логарифма;

Е_a - энергия активации, Дж/моль;

Т - температура, К;

R - газовая постоянная, 8,31 Дж/мольК.

2. Энергия активации

Для того чтобы произошла реакция, необходимо преодолеть отталкивание электронных оболочек молекул и разорвать или ослабить связи между атомами. На это надо затратить определенную энергию.

Избыточная энергия (по сравнению со средней энергией при данной температуре), которой должны обладать молекулы, для протекания реакции, называется энергией активации.

Молекулы, обладающие такой энергией, называются активными молекулами.

В ходе реакции вещества переходят в неустойчивое промежуточное состояние, характеризующееся большим запасом энергии. Именно для его образования необходима энергия активации (рис. 1, 2).

Переходным состоянием системы (или активированным комплексом) называется состояние системы реагирующих веществ, соответствующее максимальной энергии на пути реакции.

Энергия активации – это количество дополнительной энергии, необходимой для перехода системы из исходного состояния в состояние активированного комплекса.

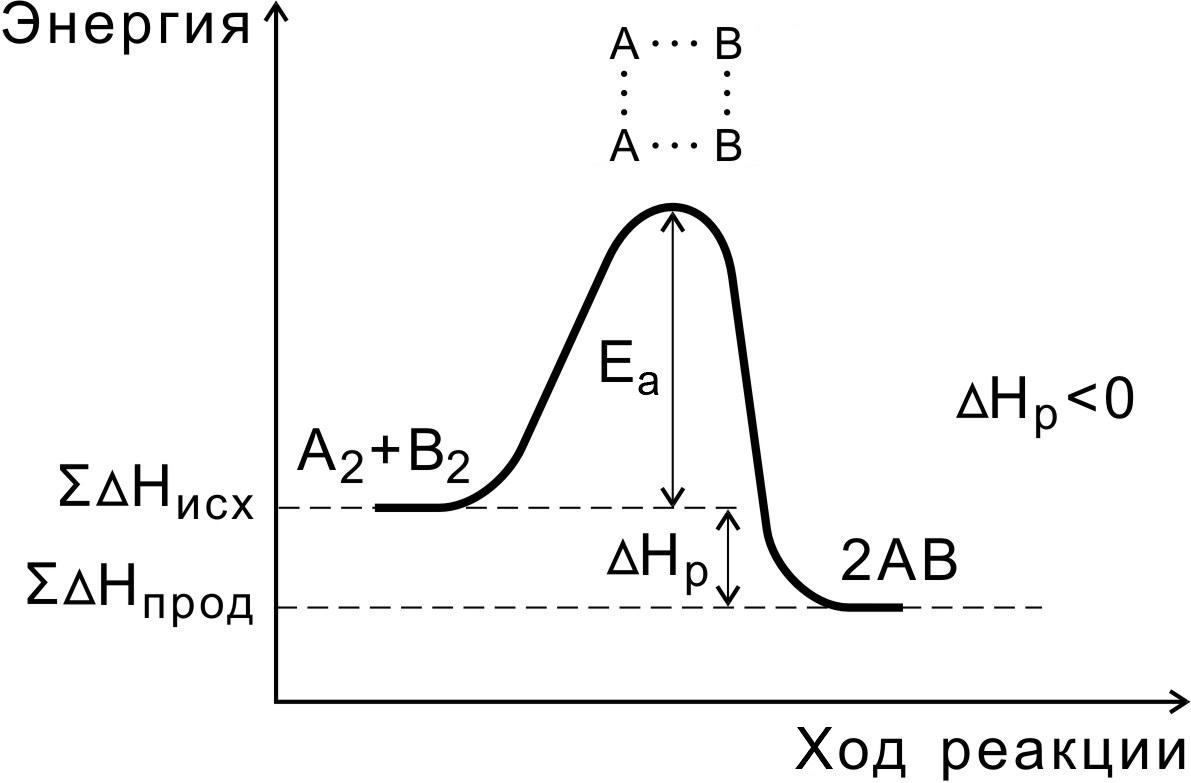
Рис. 1. Энергетическая диаграмма экзотермической реакции

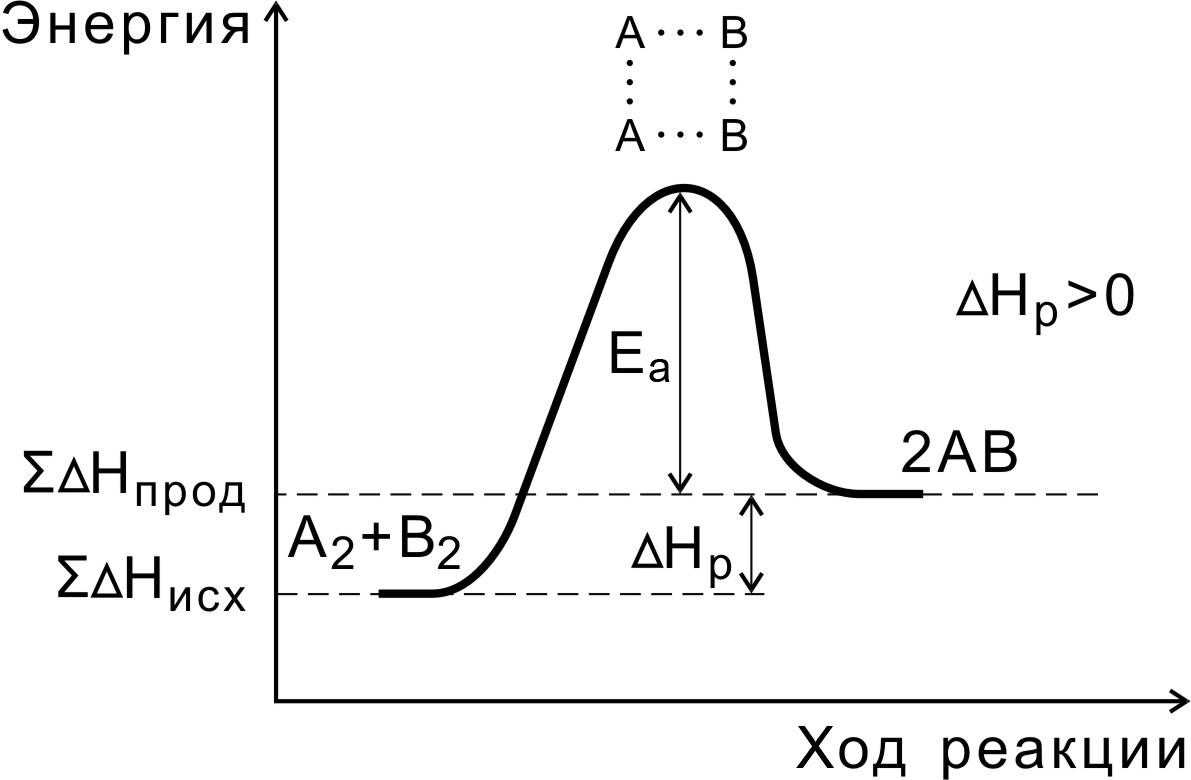
Рис. 2. Энергетическая диаграмма эндотермической реакции

Число частиц, входящих в активированный комплекс, определяет молекулярность данной стадии реакции.

В переходном состоянии старые химические связи ослаблены, но окончательно не разорваны, а новые связи начали образовываться, но еще не сформировались. Неустойчивый активированный комплекс (т.к. обладает избытком энергии) существует очень короткое время. Он распадается с образованием исходных веществ или продуктов реакции.

Переходное состояние возникает в ходе как прямой, так и обратной реакции (рис. 3). Энергетически оно отличается от исходных веществ на величину энергии активации прямой реакции, а от конечных – на энергию активации обратной реакции. Разность энергий активации прямой и обратной реакций равна изменению внутренней энергии (тепловому эффекту) реакции:

 

Н_р = Е_а - Е_а

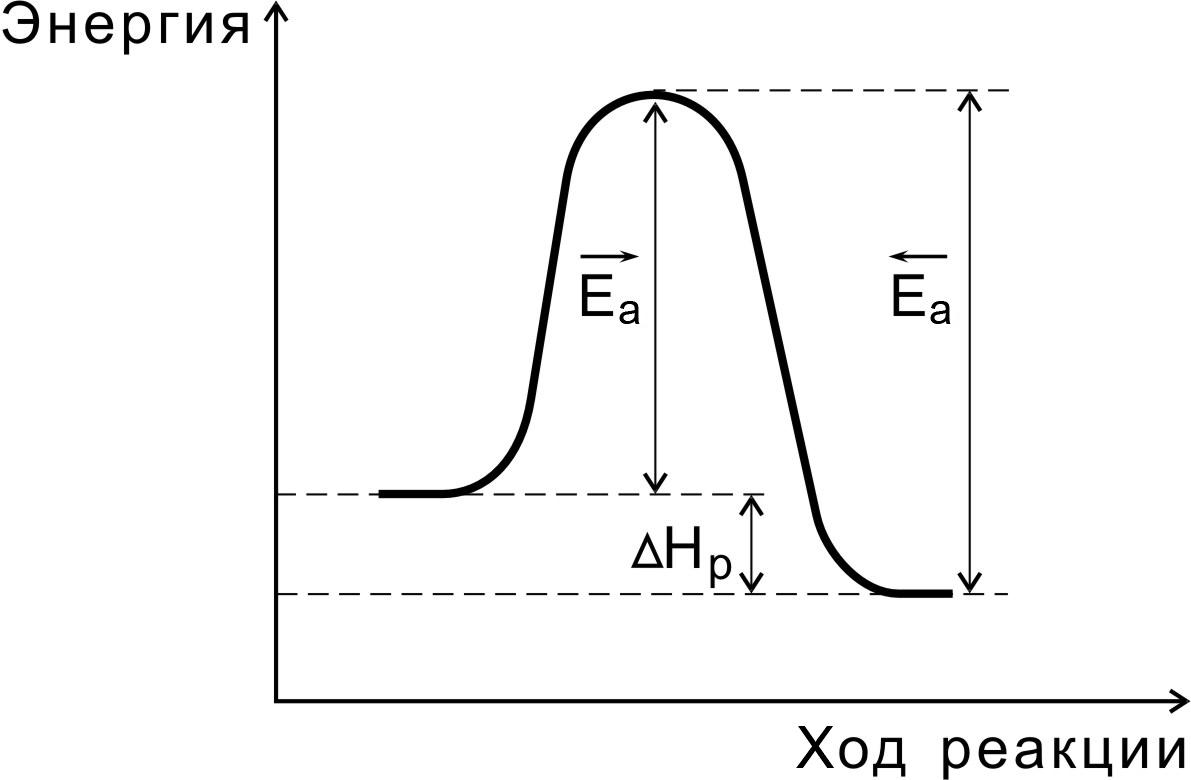
Рис.3. Соотношение между энергиями активации прямой

и обратной реакций и теплового эффекта

3. Распределение молекул по энергиям

Скорость реакции зависит от числа молекул, обладающих энергией, достаточной для образования активированного комплекса. На рис. 4 показано распределение молекул идеального газа по кинетической энергии согласно статистическому закону Максвелла-Больцмана при двух разных температурах. Доля молекул с энергией, превышающей энергию активации Еа (доля активных молекул), с повышением температуры резко возрастает (площадь заштрихованной области).

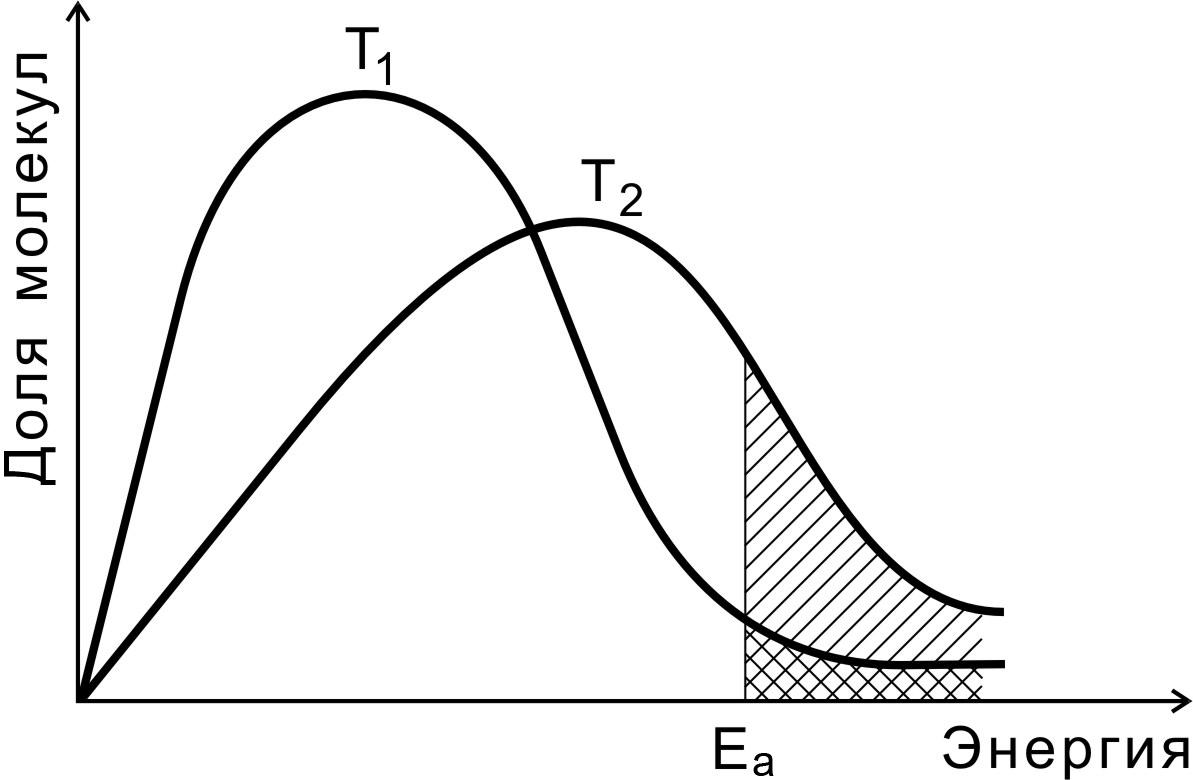
Рис. 4. Распределение молекул по энергиям

при двух разных температурах

Чем выше температура, тем больше в системе активных молекул, тем выше скорость реакции.

3. Энтропия активации. Стерический фактор

Кроме энергии активации важным условием осуществления химической реакции является ориентация молекул в момент столкновения. Большую роль играют размеры и форма молекул, место расположения реакционно-способных атомов или групп атомов в молекуле.

Например, в реакции

А₂ + B₂  2AB

ориентация (а) реагирующих частиц при столкновении будет более благоприятна, чем ориентация (б) (рис. 5).

Рис.5. Благоприятная (а) и неблагоприятная (б) ориентация

молекул при столкновении

Вероятность необходимой для взаимодействия ориентации молекул при столкновении

где, n_взаим - число способов ориентации, приводящих к взаимодействию;

n_общ - общее число возможных способов ориентации.

Энтропия активации для 1 моля по уравнению Больцмана

.

Вероятность необходимой ориентации

.

Чем больше вероятность необходимой для реакции ориентации, т.е. чем больше значение энтропии активации, и чем меньше значение энергии активации, тем выше скорость реакции и, соответственно, константа скорости:

, (2)

где Z – коэффициент пропорциональности.

Для бимолекулярных реакций Z – это число столкновений частиц в единице объема за единицу времени (1с, 1 см³).

Уравнение (2) называют основным уравнением химической кинетики. Энергия активации и энтропия активации являются теми факторами, посредством которых сказывается влияние природы реагирующих веществ на скорость реакции.

Множитель называется стерическим фактором (или стерическим множителем, или фактором вероятности).

Стерический фактор ( ) и частота столкновений (Z) учитываются в уравнении Аррениуса (1) через предэкспоненциальный множитель (А).

5. Решение уравнения Аррениуса

Энергию активации можно рассчитать по экспериментальным данным графическим или аналитическим способами, используя уравнение Аррениуса

^,

представив его в логарифмическом виде

(3)

Графический способ

По экспериментальным значениям константы скорости реакции при различных температурах строят график зависимости lnk = f () (рис. 6).

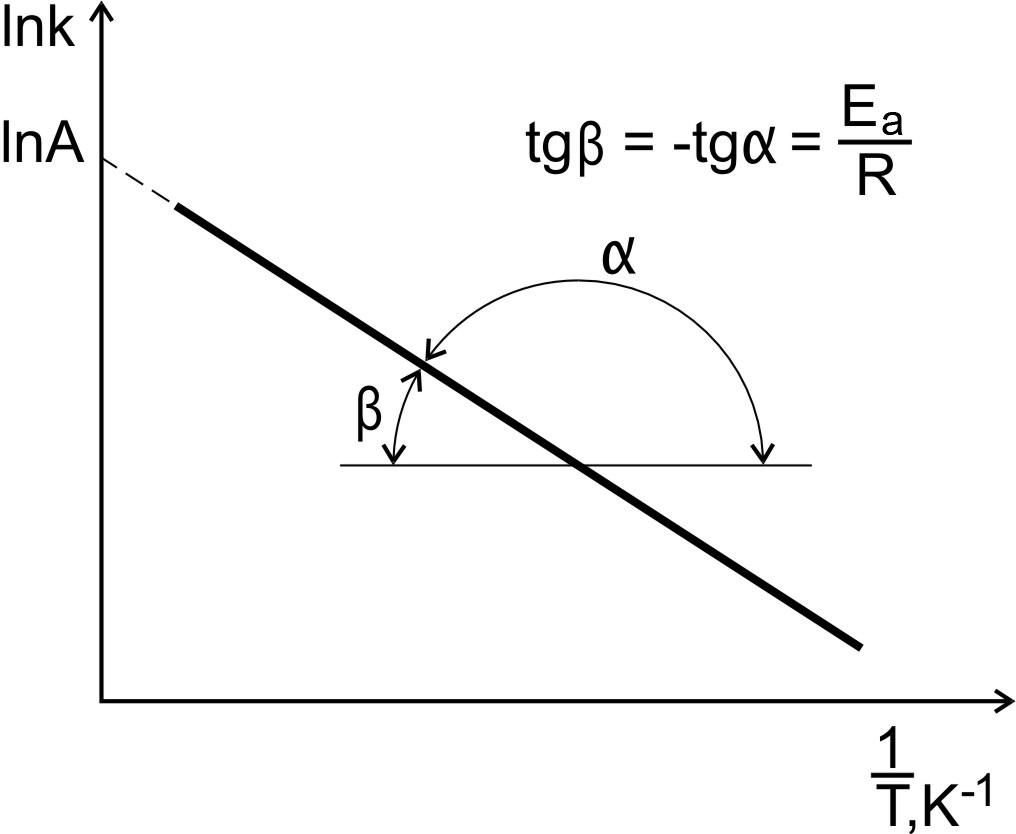
Рис. 6. Зависимость константы скорости реакции

от температуры.

По тангенсу угла наклона прямой к оси абсцисс вычисляют энергию активации

,

Отрезок, отсекаемый прямой на оси ординат при (), численно равен ln А.

Аналитический способ

Если предположить, что для выбранной реакции величины А и Е_а постоянны в небольших пределах температур от Т₁ до Т₂, то уравнение Аррениуса (3) можно применить для двух различных температур (Т₂ Т₁; k (Т₂) = k₂; k (Т₁) = k₁):

В результате вычитания первого уравнения из второго получим

,

следовательно,

.

Под символом логарифма находится отношение констант скоростей реакции при двух температурах, поэтому константы можно заменить любыми пропорциональными им величинами при тех же температурах. Например, вместо констант скоростей можно подставить скорости реакции, если исходные концентрации реагирующих веществ при измерении скоростей в обоих опытах были одинаковы, и скорость изменилась только под влиянием изменения температуры. Тогда получим следующие выражения:

;

.

Литература

1. Глинка Н.Л. Общая химия. – М.: Интеграл-Пресс, 2006. Гл.VI.

§6.2.

2. Коровин Н.В. Общая химия. – М.: Высш. шк., 2007. Гл. VII, § 7.1-7.2.

3. Глинка Н.Л. Задачи и упражнения по общей химии.- М: Интеграл-Пресс, 2006, гл.V, § 5.2.

9