Графический метод определения констант дифференциального кинетического уравнения

Определим константы дифференциального кинетического уравнения для следующей реакции:

аА + bB → продукты

Зависимость скорости от концентраций выражается уравнением (3)

.

(3)

Прологарифмируем это выражение:

.

(4)

Так как величины k, nиmдля рассматриваемой реакции (приT =const) являются постоянными и не зависят от концентрации реагентов, то для их нахождения достаточно определить зависимость скорости реакции от концентрации одного из реагентов при фиксированной концентрации другого реагента.

Пусть в трех опытах концентрация вещества А будет постоянной и равной [A]₀, тогда в уравнении (4) сумма (lnk+nln[A]₀) будет тоже величиной постоянной, обозначим ее

.

Тогда уравнение (4) можно переписать как

. (5)

Зависимость (5) представляет собой в координатах ln[B] -уравнение прямой линии, тангенс угла наклона которой численно равен порядку реакции по веществуВ.

По экспериментальным данным строят график зависимости отln[B] (рис. 3) и находят порядок реакции по веществуB:

или .

Рис.3. Определение порядка реакции по веществу В

В последующих опытах определяют скорость реакции при различных исходных концентрациях вещества Аи постоянной концентрации [B]₀. Находят порядок реакции по веществуА:

или .

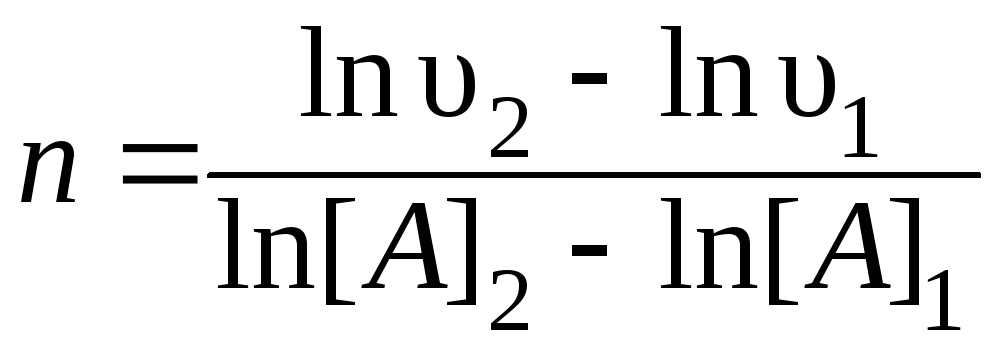Из уравнения (3) с учетом найденных порядков реакции по веществам АиВ, рассчитывают константу скоростиk:

,

где , [A]_i, [B]_i - экспериментальные данные, относящиеся к одному опыту.

4. Зависимость концентрации реагирующих веществ от времени для реакции первого порядка. Интегральное кинетическое уравнение

На практике чаще всего интересует не само значение скорости химической реакции, а то, сколько вещества израсходовано или образовалось к определенному моменту времени после начала реакции.

Рассмотрим эту задачу на примере реакции первого порядка

А продукты

Скорость такой реакции выражается следующим уравнением

(6)

В дифференциальном виде:

.

(7)

Приравняв правые части уравнений (6) и (7), получим

.

Перепишем это уравнение в следующем виде

-

и возьмем определенный интеграл от обеих частей уравнения от исходного состояния ([A]₀,t₀ = 0) до текущего момента ([A]_t,t):

.

Решение этого уравнения приводит к следующей зависимости:

(8)

или

.

(9)

По уравнению (9), зная исходную концентрацию вещества [A]₀и константу скорости реакцииk, можно рассчитать концентрацию [A]_tчерез любое времяtпосле начала реакции.

Если же известны исходная концентрация [A]₀и концентрация реагирующего вещества [A]_tчерез какое-то времяtпосле начала реакции, то можно рассчитать константу скорости этой реакции:

.

(10)

Соотношения (8) - (10) являются интегральными кинетическими уравнениямиреакции первого порядка.

Часто для характеристики скорости реакции пользуются временем полупревращения t_1/2(для реакций первого порядка чаще говорят «период полураспада»).t_1/2- это время, за которое прореагирует половина исходного вещества:. Тогда, исходя из уравнения (10), получим следующие зависимости:

;	(11)
.	(12)