11.4. Вертикальная планировка улиц с переломами в продольном профиле

При наличии в продольном профиле переломов вертикальные кривые вписываются в них лишь при алгебраической разности продольных уклонов, превышающей нормативные значения в зави­симости от расчетной скорости движения и категории улицы (табл. П.2). При строительстве земляного полотна улицы вертикальная кривая разбивается хордами 30 — 50 м при выпуклой кривой и10 — 15 м при вогнутой с превышениями в концах хорд соответст­венно 0,10 — 0,15 и 0,20 — 0,25 м. Большая точность при произ­водстве земляных работ и не требуется, так как ломаная линия в

8* 211

продольном профиле, состоящая из большого числа хорд с малой раз­ницей продольных уклонов, воспринимается зрительно как плав­ная кривая. Нарушения зрительной плавности возникают при алгеб­раической разнице уклонов в концах хорд более 15

212

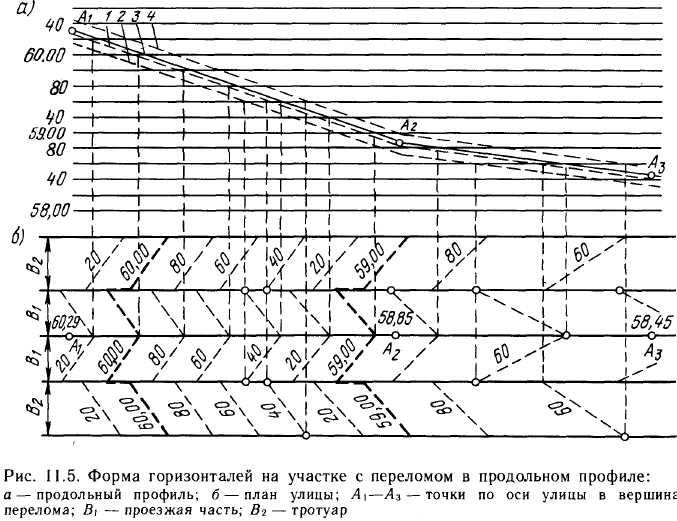
При алгебраической разнице продольных уклонов меньше нор­мативных ведущую линию на участке перелома градуируют обыч­ным образом: расстояния с обеих сторон перегона определяют с учетом продольных уклонов. Если горизонтали пересекают линию перегона, форма их меняется согласно рис. 11.5.

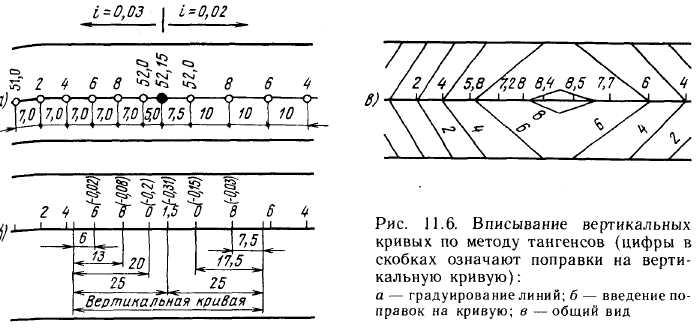
Вертикальную кривую в перелом продольного профиля можно вписать двумя способами. Первый аналогичен методу тангенсов, применяемому при проектировании продольного профиля. Согласно этому методу сначала градуируют обе ветви перелома (рис. 11.6, а), затем в точках, где расположены горизонтали, вводят поправку отметок на вертикальную кривую (рис. 11.6,6). Эти поправки вычисляют от начала кривой:

где l — расстояние от начала кривой до горизонтали, м; — радиус верти­кальной кривой, м.

Для вертикальных выпуклых кривых эти поправки вводят с минусом, для вогнутых — с плюсом. После ввода поправок все горизонтали в пределах вертикальной кривой будут иметь дробные отметки. Положение горизонталей, кратных сечению, определяют интерполяцией (рис. 11.6, в).

Второй способ позволяет рассчитывать положение проектных горизонталей сразу с учетом вертикальной кривой. При этом ис­пользуют положение о симметричности кривой относительно вер­тикали, проходящей через ее вершину. Расчет ведут в такой после­довательности: сначала находят положение вершины кривой и ее отметку, а затем, идя от вершины, находят положение проектных горизонталей.

где— продольный уклон в начале кривой.

Положение вершины можно найти расчетом согласно рис. 11.7. Положение кривой, ее начало и конец определяют алгебраической разностью продольных уклонов и радиуса кривой. Обе ветви пере­лома градуируют до вертикальной кривой и определяют отметки ее начала и конца. Расстояние от начала кривой до вершины

213

Превышение вершины над началом кривой . О

метку вершины кривой определяют с помощью отметки ее нача, . и превышения. Расстояние от вершины кривой до

первой проектной горизонтали

где— разница отметок вершины кривой и первой горизонтали, м.

Расстояние от вершины кривой до следующих горизонталей

где п — номер горизонтали, считая от вершины.

Значения откладывают в обе стороны от вершины кривой. Наибольшее значение /_п равно расстоянию от вершины для начала кривой (). По мере удаления от вершины кривой расстояния между горизонталями уменьшаются.

Положение проектных горизонталей на вертикальной кривой может быть определено с помощью таблиц для проектирования-кривых в продольном профиле. Последовательность проектиров; ния при этом не изменяется; таблицы позволяют без вычислени определять превышения на кривой и расстояния между горизонта-лями при заданных продольных уклонах. В таблицах для конкреп ного радиуса вертикальной кривой в одной строке показаны превы-шение точки над вершиной, расстояние от вершины и продольны уклон в этой точке.

214

В табл. 11.3 приведены эти данные для кривой радиусом 1000 м Этой таблицей можно пользоваться и при других радиусахвер тикальных кривых. Для этого необходимо ввести поправку

Поправку вводят в / и i, превышениенад вершиной кривой остается неизменным:

гдеи— значения расстояния от вершины и продольного уклона соответст­венно при заданном из табл. 11.3 для=1000 м.