Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский автомобильно-дорожный государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

626266

.pdf

Скачиваний:

Добавлен:

16.05.2015

Размер:

7.64 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 275 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

	1
6.	y		ln(tgx ctg ).
		sin
	1
1.	y		ln(tgx ctg ).
		sin
	1
2.	y		ln(tgx ctg ).
		sin
	1
3.	y		ln(tgx ctg ).
		sin
	1
4.	y		ln(tgx ctg ).
		sin
	1
5.	y		ln(tgx ctg ).
		sin
	1
6.	y		ln(tgx ctg ).
		sin

31. y 1 ln(tgx ctg ). sin

Задача 15. Найти производную

		3t 2		1
	x					,
	x		3t	3		,
			3t
1.			t 3
			t 3
	y sin						t .
	y sin						t .

			3
			3
			3t 2		1
	x							,
	x		3t		3			,
			3t
2.				t 3
				t 3
	y sin							t .
	y sin							t .

				3
				3
			3t 2		1
	x							,
	x		3t		3			,
			3t
3.				t 3
				t 3
	y sin							t .
	y sin							t .

				3
				3
			3t 2		1
	x							,
	x		3t		3			,
			3t
4.				t 3
				t 3
	y sin							t .
	y sin							t .

				3
				3
			3t 2		1
	x							,
	x		3t		3			,
			3t
5.				t 3
				t 3
	y sin							t .
	y sin							t .

				3
				3

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

y .

		3t 2		1
	x				,
	x	3t		3	,
		3t
6.			t 3
			t 3
	y sin				t .
	y sin				t .

			3
			3
		3t 2		1
	x				,
	x	3t		3	,
		3t
7.			t 3
			t 3
	y sin				t .
	y sin				t .

			3
			3
		3t 2		1
	x				,
	x	3t		3	,
		3t
8.			t 3
			t 3
	y sin				t .
	y sin				t .

			3
			3
		3t 2		1
	x				,
	x	3t		3	,
		3t
9.			t 3
			t 3
	y sin				t .
	y sin				t .

			3
			3

	3t 2 1
x			,
	3t	3

10.	t 3

y sin			t .


	3

11.

12.

13.

14.

15.

16.

17.

18.

19.


	3t 2	1		,
	3t 3			,
	3t 3
		t 3
sin				t .
sin				t .
			3
			3
	3t 2	1		,
	3t 3			,
	3t 3
		t 3
sin				t .
sin				t .
			3
			3
	3t 2	1		,
	3t 3			,
	3t 3
		t 3
sin				t .
sin				t .
			3
			3
	3t 2	1		,
	3t 3			,
	3t 3
		t 3
sin				t .
sin				t .
			3
			3
	3t 2	1		,
	3t 3			,
	3t 3
		t 3
sin				t .
sin				t .
			3
			3
	3t 2	1		,
	3t 3			,
	3t 3
		t 3
sin				t .
sin				t .
			3
			3
	3t 2	1		,
	3t 3			,
	3t 3
		t 3
sin				t .
sin				t .
			3
			3
	3t 2	1		,
	3t 3			,
	3t 3
		t 3
sin				t .
sin				t .
			3
			3
	3t 2	1		,
	3t 3			,
	3t 3
		t 3
sin				t .
sin				t .
			3
			3

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

	3t 2		1
x				,
	3t		3

20.		t 3

y sin				t .


		3

	3t 2		1
x				,
	3t		3

21.		t 3

y sin				t .


		3

	3t 2		1
x				,
	3t		3

22.		t 3

y sin				t .


		3

	3t 2		1
x				,
	3t		3

23.		t 3

y sin				t .


		3

	3t 2		1
x				,
	3t		3

24.		t 3

y sin				t .


		3

	3t 2		1
x				,
	3t		3

25.		t 3

y sin				t .


		3

	3t 2		1
x				,
	3t		3

26.		t 3

y sin				t .


		3

	3t 2		1
x				,
	3t		3

27.		t 3

y sin				t .


		3

	3t 2		1
x				,
	3t		3

28.		t 3

y sin				t .


		3

	3t 2		1
x				,
	3t		3

29.		t 3

y sin				t .


		3

	3t 2		1
x				,
	3t		3

30.		t 3

y sin				t .


		3

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

	3t 2 1
x			,
	3t	3

31.	t 3

y sin			t .


	3

Задача 16. Составить уравнения касательной и нормали к кривой в точке, соответствующей значению

параметра t t0 .
	x a sin 3 t,				x a sin 3 t,

1.				12.
	y a cos3 t, t	0	/ 3.		y a cos	3 t, t		0	/ 3.
		0						0
					x a sin 3 t,

	x a sin 3 t,			13.		3	t, t		/ 3.
					y a cos		t, t	0	/ 3.
2.			/ 3.					0
	y a cos3 t, t		/ 3.		x a sin 3 t,
		0			x a sin 3 t,

	x a sin 3 t,			14.		3	t, t		/ 3.
					y a cos		t, t	0	/ 3.
3.			/ 3.					0
	y a cos3 t, t		/ 3.		x a sin 3 t,
		0			x a sin 3 t,

	x a sin 3 t,			15.		3	t, t		/ 3.
					y a cos		t, t	0	/ 3.
4.			/ 3.					0
	y a cos3 t, t		/ 3.		x a sin 3 t,
		0			x a sin 3 t,

	x a sin 3 t,			16.		3	t, t		/ 3.
					y a cos		t, t	0	/ 3.
5.			/ 3.					0
	y a cos3 t, t		/ 3.		x a sin 3 t,
		0			x a sin 3 t,

	x a sin 3 t,			17.		3	t, t		/ 3.
					y a cos		t, t	0	/ 3.
6.			/ 3.					0
	y a cos3 t, t		/ 3.		x a sin 3 t,
		0			x a sin 3 t,

	x a sin 3 t,			18.		3	t, t		/ 3.
					y a cos		t, t	0	/ 3.
7.			/ 3.					0
	y a cos3 t, t		/ 3.		x a sin 3 t,
		0			x a sin 3 t,

	x a sin 3 t,			19.		3	t, t		/ 3.
					y a cos		t, t	0	/ 3.
8.			/ 3.					0
	y a cos3 t, t		/ 3.		x a sin 3 t,
		0			x a sin 3 t,

	x a sin 3 t,			20.		3	t, t		/ 3.
					y a cos		t, t	0	/ 3.
9.			/ 3.					0
	y a cos3 t, t		/ 3.		x a sin 3 t,
		0			x a sin 3 t,

	x a sin 3 t,			21.		3	t, t		/ 3.
					y a cos		t, t	0	/ 3.
10.								0
	y a cos3 t, t			/ 3.	x a sin 3 t,
			0		x a sin 3 t,

	x a sin 3 t,			22.		3	t, t		/ 3.
					y a cos		t, t	0	/ 3.
11.								0
	y a cos3 t, t		0	/ 3.
			0

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

x a sin 3 t,			x

23.		28.
y a cos3 t, t	0	/ 3.	y
	0
x a sin 3 t,			x

24.		29.
y a cos3 t, t	0	/ 3.	y
	0
x a sin 3 t,			x

25.		30.
y a cos3 t, t	0	/ 3.	y
	0
x a sin 3 t,			x

26.		31.
y a cos3 t, t	0	/ 3.	y
	0
x a sin 3 t,

27.
y a cos3 t, t	0	/ 3.
	0

a sin 3 t,

a cos3 t, t0 / 3.

a sin 3 t,

a cos3 t, t0 / 3.

a sin 3 t,

a cos3 t, t0 / 3.

a sin 3 t,

a cos3 t, t0 / 3.

Задача 17. Найти производную n -го порядка.
1.	y xeax .	17.	y xeax .
2.	y xeax .	18.	y xeax .
3.	y xeax .	19.	y xeax .
4.	y xeax .	20.	y xeax .
5.	y xeax .	21.	y xeax .
6.	y xeax .	22.	y xeax .
7.	y xeax .	23.	y xeax .
8.	y xeax .	24.	y xeax .
9.	y xeax .	25.	y xeax .
10.	y xeax .	26.	y xeax .
11.	y xeax .	27.	y xeax .
12.	y xeax .	28.	y xeax .
13.	y xeax .	29.	y xeax .
14.	y xeax .	30.	y xeax .
15.	y xeax .	31.	y xeax .
16.	y xeax .

Задача 18. Найти производную указанного порядка.

1.	y (2x2	7) ln(x 1),	y5	? .	4.	y (2x2	7) ln(x 1),	y5	? .
2.	y (2x2	7) ln(x 1),	y5	? .	5.	y (2x2	7) ln(x 1),	y5	? .
3.	y (2x2	7) ln(x 1),	y5	? .	6.	y (2x2	7) ln(x 1),	y5	? .

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

7.y (2x2 7) ln(x 1), y5 ? .

8.y (2x2 7) ln(x 1), y5 ? .

9.y (2x2 7) ln(x 1), y5 ? .

10.y (2x2 7) ln(x 1), y5 ? .

11.y (2x2 7) ln(x 1), y5 ? .

12.y (2x2 7) ln(x 1), y5 ? .

13.y (2x2 7) ln(x 1), y5 ? .

14.y (2x2 7) ln(x 1), y5 ? .

15.y (2x2 7) ln(x 1), y5 ? .

16.y (2x2 7) ln(x 1), y5 ? .

17.y (2x2 7) ln(x 1), y5 ? .

18.y (2x2 7) ln(x 1), y5 ? .

19.y (2x2 7) ln(x 1), y5 ? .

Задача 19. Найти производную второго порядка

x cos 2t,
1.	2	.
y 2sec	2	t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

20.y (2x2 7) ln(x 1), y5 ? .

21.y (2x2 7) ln(x 1), y5 ? .

22.y (2x2 7) ln(x 1), y5 ? .

23.y (2x2 7) ln(x 1), y5 ? .

24.y (2x2 7) ln(x 1), y5 ? .

25.y (2x2 7) ln(x 1), y5 ? .

26.y (2x2 7) ln(x 1), y5 ? .

27.y (2x2 7) ln(x 1), y5 ? .

28.y (2x2 7) ln(x 1), y5 ? .

29.y (2x2 7) ln(x 1), y5 ? .

30.y (2x2 7) ln(x 1), y5 ? .

31.y (2x2 7) ln(x 1), y5 ? .

от функции, заданной параметрически.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

x cos 2t,

y 2sec2 t.

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

	x cos 2t,				x cos 2t,
19.		2		26.		2
	y 2sec	2	t.		y 2sec	2	t.
	x cos 2t,				x cos 2t,
20.		2		27.		2
	y 2sec	2	t.		y 2sec	2	t.
	x cos 2t,				x cos 2t,
21.		2		28.		2
	y 2sec	2	t.		y 2sec	2	t.
	x cos 2t,				x cos 2t,
22.		2		29.		2
	y 2sec	2	t.		y 2sec	2	t.
	x cos 2t,				x cos 2t,
23.		2		30.		2
	y 2sec	2	t.		y 2sec	2	t.
	x cos 2t,				x cos 2t,
24.		2		31.		2
	y 2sec	2	t.		y 2sec	2	t.

x cos 2t,

y 2sec2 t.

Задача 20. Показать, что функция y удовлетворяет данному уравнению.

1.y xe x2 / 2 . xy (1 x2 ) y.

2.y xe x2 / 2 . xy (1 x2 ) y.

3.y xe x2 / 2 . xy (1 x2 ) y.

4.y xe x2 / 2 . xy (1 x2 ) y.

5.y xe x2 / 2 . xy (1 x2 ) y.

6.y xe x2 / 2 . xy (1 x2 ) y.

7.y xe x2 / 2 . xy (1 x2 ) y.

8.y xe x2 / 2 . xy (1 x2 ) y.

9.y xe x2 / 2 . xy (1 x2 ) y.

10.y xe x2 / 2 . xy (1 x2 ) y.

11.y xe x2 / 2 . xy (1 x2 ) y.

12.y xe x2 / 2 . xy (1 x2 ) y.

13.y xe x2 / 2 . xy (1 x2 ) y.

14.y xe x2 / 2 . xy (1 x2 ) y.

15.y xe x2 / 2 . xy (1 x2 ) y.

16.y xe

17.y xe

18.y xe

19.y xe

20.y xe

21.y xe

22.y xe

23.y xe

24.y xe

25.y xe

26.y xe

27.y xe

28.y xe

29.y xe

30.y xe

31.y xe

/2 .

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y. xy (1 x2 ) y.

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

§ 3.1. ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ

1)Условия возрастания функции на отрезке.

2)Условия убывания функции на отрезке.

3)Точки экстремума. Необходимое условие экстремума.

4)Достаточные признаки максимума и минимума функции (изменение знака первой производной).

5)Наибольшее и наименьшее значения функции, непрерывной на отрезке.

6)Выпуклость и вогнутость графика функции. Достаточные условия выпуклости и вогнутости.

7)Точки перегиба графика функции. Необходимое условие перегиба. Достаточные условия перегиба,

8)Исследование функции на экстремум с помощью высших производных.

9)Асимптоты графика функции.

§3.2. ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ

1) Доказать, что функция f (x) x sin x монотонно возрастает на отрезке: а) [ 0 , 2 ]; б) [ 0,4 ].

Следует ли из монотонности дифференцируемой функции монотонность ее производной?

2) Доказать теорему: если функции (x) и (x) дифференцируемы на отрезке [a,b] и (x) > (x)

x (a,b) , а (a) = (a) , то (x) > (x) x a,b .

Дать геометрическую интерпретацию теоремы.

Указание. При доказательстве теоремы установить и использовать монотонность функции

f (x) (x) (x) .

3) Доказать неравенство 2x sin x для трех случаев:

a) x 0, arccos

; б) x arccos

, f); в)

x 0,

Дать геометрическую интерпретацию неравенства.

4) Исходя из определений минимума и максимума, доказать, что функция

1/ x2

, x 0,

f (x)

0, x 0

имеет в точке x = 0 минимум, а функция

1/ x2

, x 0,

g(x)

0, x 0

не имеет в точке x = 0 экстремума.

5) Исследовать

на

экстремум

в точке

функцию

f (x) (x x

)n (x) , считая, что производная

(x) не существует, но функция (x) непрерывна в точке

x0 и (x0 ) 0 ,

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

n— натуральное число.

6)Исследовать знаки максимума и минимума функции x3 3x q и выяснить условия, при которых уравнение x3 3x q имеет:

а) три различных действительных корня;
б) один действительный корень.
7)	Определить «отклонение от нуля» многочлена	p(x) 6x3		27x2	36x 14 на отрезке [0,3], т. е.
найти	на этом отрезке наибольшее значение функции	p(x)	.
найти	на этом отрезке наибольшее значение функции	p(x)	.

8) Установить условия существования асимптот у графика рациональной функции.

§ 3.3. РАСЧЕТНЫЕ ЗАДАНИЯ

Задача 1. Построить графики функций с помощью производной первого порядка.

1.		y 2x3	9x2 12x 9 .	17.	y 12x2	8x3 2 .
2.	y 3x x3 .			18.	y (2x 1)2 (2x 3)2 .
3.	y x2 (x 2)2 .			19.	y 27(x3 x2 ) / 4 4 .
4.	y (x3 9x2 ) / 4 6x 9. .			20.	y x(12 x2 ) / 8 .
5.	y 2 3x2 x3 .			21.	y x2 (x 4)2 /16 .
6.	y (x 1)2 (x 1)2 .			22.	y 27(x3 x2 ) / 4 5.
7.	y 2x3		3x2 4 .	23.	y (16 6x2 x3 ) / 8 .
8.	y 3x2		2 x3 .	24.	y (x2	4)2 /16 .
9.	y (x 1)2 (x 3)2 .			25.	y 16x3	36x2 24x 9 .
10.		y (x3	3x2 ) / 4 5.	26.	y (6x2	x3 16) / 8 .
11.		y 6x 8x3 .		27.	y (x 2)2 (x 6)2 /16 .
12.		y 16x2 (x 1)2 .		28.	y 16x3	12x2 4 .
13.		y 2x3 3x2 5 .		29.	y (11 9x 3x2 x3 ) / 8 .
14.		y 2 12x2 8x3 .		30.	y (x 1)2 (x 3)2 /16 .
15.		y (2x 1)2 (2x 1)2 .		31.	y 16x3	12x2 5.
16.		y 2x3 9x2 12x .

Задача 2. Построить графики функций с помощью производной первого порядка.


1. y 1 3 x2 2x.			2. y 2x 33 x2 .

3.y 123 6(x 2)2 .

x2 8

123 6(x 1)2 4. y x2 2x 9 .

5.y 1 3 x2 2x.

6.y 2x 6 33 (x 3)2 .


7. y	63 6(x 3)2	.

	x 2 2x 9

8.y 1 3 x2 4x 3.

9.y 33 (x 3)2 2x 6.

63 6x2

10.

4x 12

11.

y 4x 8 63 (x 2)2 .

12.

6(x 4)2

x 2 4x 12

13.

y 3

x(x 2).

14.

y 3

4x 3.

15.

6(x 1)2

6x 17

16.

y 63

(x 2)2 4x 8.

17.

6(x 5)2

x 2

6x 17

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

18.y 2 3 8x(x 2).

19.y 6x 6 93 (x 1)2 .

20.y 3 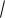x2 6x 8.

21.y 3 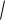4x(x 1).


22.	y			33					6(x 2)2		.

				x2 8x 24

23.	y 3			x(x 2).

24.	y 1 3								x2 4x 3.

25.	y 93				(x 1)2 6x 6.

26.	y	63				6(x 3)2
			x 2		10x 33


27.	y 8x 16 123 (x 2)2 .

28.	y			63					6(x 6)2	.

				x 2 8x 24

29.	y 123						(x 2)2 8x 16.

30.	y		33					6(x 1)2				.

			2(x2 2x 9)

31.	y 33				(x 4)2 2x 8.

Задача 3. Найти наибольшее и наименьшее значения функций на заданных отрезках.

1.y x2 16x 16, 1,4 .

2.y 4 x x42 , 1,4 .

3.y 3 2(x 2)2 (8 x) 1, 0,6 .

4. y	2(x2 3)	, 3,3 .
	x2 2x 5

5. y 2 x x, 0,4 .

6.y 1 3 2(x 1)2 (x 7), 1,5 .

7.y x 4x 5, 1,9 .

8. y	10x	, 0,3 .
	1 x2

9.y 3 2(x 1)2 (5 x) 2, 3,3 .

10.y 2x2 108x 59, 2,4 .

11. y 3 x	4	, 1,2 .

	(x 2)2

<<< < Предыдущая 1 2 3 45 / 275 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.03.2025121.29 Кб05ballov-75211.rtf
#
05.08.2019164.54 Кб96-16.docx
#
01.05.202566.61 Кб06. Экономическая часть.docx
#
23.09.201942.43 Кб660-82.docx
#
01.04.202599.33 Кб061-66_2novoe.doc
#
16.05.20157.64 Mб28626266.pdf
#
25.09.2019240.63 Кб1364-70, 115.docx
#
22.09.2019604.67 Кб1166-100.doc
#
01.04.2025573.66 Кб166-73.docx
#
23.09.201979.32 Кб127-12.docx
#
16.05.201547.79 Кб2671-80.docx