Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский автомобильно-дорожный государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

626266

.pdf

Скачиваний:

Добавлен:

16.05.2015

Размер:

7.64 Mб

Скачать

☆

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2719 20 21 22 23 24 25 26 27 > Следующая >>>

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

2.Проектирования на плоскость z 0 .

3.Проектирования на ось Oz .

4.Зеркального отражения относительно плоскости Oyz .

5.Проектирования на ось Oy .

6.Проектирования на плоскость y 0 .

7.Зеркального отражения относительно плоскости x y 0 .

8.Зеркального отражения относительно плоскости y z 0 .

9.Проектирования на плоскость y z 0 .

10.Проектирования на плоскость y 3x .

11.Проектирования на плоскость Oyz .

12.Зеркального отражения относительно плоскости x z 0 .

13.Зеркального отражения относительно плоскости Oxy .

14. Поворота относительно оси Ox на угол 2 в положительном направлении.

15.проектирования на плоскость x y 0 .

16.проектирования на плоскость y z 0 .

17.зеркального отражения относительно плоскости x y 0 .

18.зеркального отражения относительно плоскости y z 0 .

19.проектирования на плоскость x y 0 .

20.проектирования на плоскость x z 0 .

21.зеркального отражения относительно плоскости x z 0 .

22.поворота относительно оси Oz в положительном направлении на угол 2 .

23.проектирования на плоскость 3y z 0 .

24.зеркального отражения относительно плоскости Oxz .

25.поворота в положительном направлении относительно оси Oy на угол 2 .

26.проектирования на плоскость x z 0 .

27.проектирования на плоскость y 3z 0 .

28.проектирования на плоскость 3x z 0 .

29.проектирования на плоскость 3x y 0 .

30.поворота относительно оси Oz в положительном направлении на угол 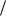4 .

31.проектирования на плоскость x 3z 0 .

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

Задача 9. Найти собственные значения и собственные векторы матрицы.

4			2		1

1.	1		3		1 .
	1		2		2
	1		2		2
2			1		0
	1
2.	1		2		0	.
	1		1		1
	1		1		1
3			1	1

3.	0		2	1 .
	0		1	2
	0		1	2
5			1	1

4.	0		4	1 .
	0		1	4
	0		1	4
6			2		1

5.	1		5		1 .
	1		2		4
	1		2		4
3			1	1

6.		2	2	1 .
	2		1	4
	2		1	4
2			0	1

7.	1		1	1 .
	1		0	2
	1		0	2
2			1	0
	1
8.	1		2	0	.
	1		1	3
	1		1	3
4			1	0

9.	1		4	0	.
	1		1	5
	1		1	5
	5		1		1

10.		2	4		1 .
		2 1			6
		2 1			6
	5		4		4

11.		2	1		2	.
		2	0		3
		2	0		3

3		2		2
		1
12.	2	1		2	.
	2	2		3
	2	2		3
3		2		2

13.	0	3		0	.
	0	2		1
	0	2		1
5		2		2

14.	0	5		0	.
	0	2		3
	0	2		3
7		4		4

15.	2	3		2	.
	2	0		5
	2	0		5
7		6		6
		1
16.	4	1		4	.
	4	2		5
	4	2		5
7		6		6

17.	2	3		2	.
	2	2		3
	2	2		3
13		2		2
				6
18.	6	9		6			.
	2	2			5
	2	2			5
7		2	2
			2
19.	4	5	2		.
	0	0		3
	0	0		3
9		0		0
				4
20.	2	7		4		.
	2	2		5
	2	2		5
15		0			0
				4
21.	2	13		4			.
	2	2			11
	2	2			11
19		2		2
				6
22.	6	15		6			.
	2	2			11
	2	2			11

4		1		1

23.	2	3			2	.
	1	1		2
	1	1		2
2		1	1

24.	1	2	1 .
	0	0		1
	0	0		1
3		0		0

25.	1	2			1 .
	1	1
	1	1		2
5		0		0

26.	1	4			1 .
	1	1
	1	1		4
6		1		1

27.	2	5			2	.
	1	1		4
	1	1		4
9		6			6

28.	2		5		2 .
	2		2
	2		2		13
5		2			4

29.	0		3			0	.
	2		2			7
	2		2			7
7		4			2
	2				2
30.	2		5		2		.
	0		0			9
	0		0			9
	4	3		3

31.	1	2		1	.
	1	1		2
	1	1		2

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

Задача 10. Привести квадратичную форму к каноническому виду методом Лагранжа.
1.	x2		4x x					2		4x x				4x			2	x	3	4x2 .				17.	x2	2x x				2x x				5x2				10x x					4x2.
		1			1			2			1	3					2		3			3			1		1	2			1	3					2			2	3			3
2.	4x2			4x x						8x x				3x2				4x2.						18.	x2	4x x				2x x				5x2				6x x				x2.
			1			1			2		1	3				2					3				1		1	2			1	3					2		2	3			3
3.	4x2			8x x						4x x				x2.										19.	x2	4x x				x2 2x x							4x2.
			1			1		2			1	3			3										1		1	3			2				2	3			3
4.	4x2			8x x						4x x				3x2				2x2.						20.	x2	2x x				2x x				2x2				4x x				x2.
			1			1		2			1	3				2					3				1		1	2			1	3					2		2	3			3
5.	x2		4x x						4x x				3x2				4x x					x2.		21.	x2	4x x				4x x				4x				x	2x2.
		1			1	2					1	3			2					2	3		3		1		1	2			1	3					2	3		3
6.	x2		4x x						4x x				x2.											22.	4x2		4x x				4x x				3x2				2x2.
		1			1	2					2	3			3											1		1	2			1	3					2		3
7.	x2		2x x						2x x				3x2				6x x					2x2.		23.	4x2		8x x				4x x				x2.
		1			1	2					1	3			2					2	3		3			1		1	2			1	3				3
8.	x2		4x x						2x x				3x2				2x x					x2.		24.	4x2		8x x				4x x				3x2				4x2.
		1			1	2					1	3			2					2	3		3			1		1	2			1	3					2		3
9.	x2		4x x						x2 2x x 4x2.															25.	x2	4x x				4x x				3x2				4x x				x2.
		1			1	3					2			2	3					3					1		1	2			1	3					2		2	3			3
10.		x2		2x x						2x x				x2.										26.	x2	4x x				4x x				x2.
		1				1		2			1	3			3										1		1	2			1	3				3
11.		x2		4x x						4x x				8x2				12x				x	4x2.	27.	x2	2x x				2x x				3x2				6x x				4x2.
		1				1		2			1	3				2					2	3	3		1		1	2			1	3					2		2	3			3
12.		4x2			4x x						8x x				5x2				8x			x	4x2.	28.	x2	4x x				2x x				3x2				2x x				x2.
			1				1			2		1	3					2			2	3	3		1		1	2			1	3					2		2	3			3
13.		4x2			8x x						4x x				8x2				8x			x	x2.	29.	x2	4x x				x2 2x x							2x2.
			1				1			2		1	3					2			2	3	3		1		1	2			2				2	3			3
14.		4x2			8x x						4x x				5x2				8x			x	4x2.	30.	x2	2x x				2x x				x2.
			1				1			2		1	3					2			2	3	3		1		1	2			1	3				3
15.		x2		4x x						4x x				5x2				12x				x	7x2.	31.	x2	2x x				2x x				2x2				4x x				3x2.
		1				1		2			1	3				2					2	3	3		1		1	2			1	3					2		2	3			3
16.		x2		4x x						4x x				8x2				16x				x	7x2.
		1				1		2			1	3				2					2	3	3

Задача 11. Привести квадратичную форму к каноническому виду ортогональным преобразованием.

1.4x22 3x32 4x1 x2 4x1 x3 8x2 x3 .

2.4x12 4x22 x32 2x1x2 23x2 x3.

3.2x12 2x2 2x32 8x1x2 8x1x3 8x2 x3.

4.2x12 9x22 2x32 4x1x2 4x2 x3.

5.4x12 4x22 2x32 4x1x2 8x1x3 8x2 x3.

6.x12 x22 4x32 2x1x2 23x2 x3.

7.4x12 4x22 x32 2x1x2 4x1x3 4x2 x3.

8.3x12 x22 32 x32 23x1x2 x1x3 3x2 x3.

9.x12 x22 3x32 2x1x2 6x1x3 6x2 x3.

10.x12 7x22 x32 4x1x2 2x1x3 4x2 x3.

11.


5 2		x2	5 2		x2	3 2		x2		2		x x x x x x .

4	1		4	2		2	3		2		1		2	1	3	2	3

12.3x12 7x22 3x32 8x1x2 8x1x3 8x2 x3.

13.x12 5x22 x32 4x1x2 52x1x3 2x2 x3.


14.	x2	x2	x2	4	x x		8		2	x x .
14.	x2	x2	x2		x x					x x .
	1	2	3	3	1	2		3	2		3

15.2x12 2x22 2x32 4x1x2 52x1x3 2x2 x3.

16.12 x12 5x22 12 x32 4x1x2 3x1x3 4x2 x3.

17.x12 x22 x32 4x1x3 4x2 x3.

18.2x12 2x22 2x32 4x1x2 6x1x3 4x2 x3.

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

	2x2			3x2		2x2 8x x																													x2 x2 8x x 4
19.	2x2			3x2		2x2 8x x											4							2x x 2								2x x .		26.	x2 x2 8x x 4								2x x				2			2x x .
	1				2				3					1	2											1	3				2		3		1		3		1	2				1		3						2	3
20.	4x2 x2 4x2											4x x						4x x									4x x .							27.	5x2	13x2 5x2 4x x										8x x .
				1	2				3						1		2				1				3				2		3				1		2			3			1	2				2		3
21. 10x2 14x2							7x2
21. 10x2 14x2							7x2						10x x												2x x				5 2x x .						2x2	2x2		2x2				2						4	2
	1					2			3								1	2									1 3						2 3	28.									x x							x x .
																																		28.								3	x x					3		x x .
		3						3																											1		2			3		3	1	2				3				2	3
22.		3	x2	5x2				3	x2			4x x						x x								4x x .
22.			x2	5x2					x2			4x x						x x								4x x .									5x2	4x2		2x2			4x x				2 2x x								4
	2 1				2		2		3						1		2				1 3						2				3			29.	5x2	4x2		2x2			4x x				2 2x x								4	2x x .
																																			1		2			3			1	2						1		3		2	3
		x12 x22			2x32 4x1x2										2												2
23.		x12 x22			2x32 4x1x2										2					2x1x3							2			2x2 x3.				30.	2x2		5x2		2x2			4x x					4x x .
																																				1		2			3			1	2				2		3
	2x2			3x2		2								4x x									4												3x2		9x2		3x2			2x x					8x x					4x x .
24.	2x2			3x2		2				3x x				4x x									4					3x x .						31.	3x2		9x2		3x2			2x x					8x x					4x x .
	2				3							1	2					1	3								2		3							1		2			3			1	2			1		3			2	3

25.		x2 x2			x2				4		x x					8			2			x x .
25.		x2 x2			x2						x x											x x .
	1			2		3			3			1	2					3			2					3

Задача 12. Исследовать кривую второго порядка и построить ее.


1.	x2 y 2					4xy 2x 4y 1 0.			17.	3x2 3y2	2xy 6x 2y 1 0.
2.	2x2 2y2					2xy 2x 2y 1 0.			18.	4xy 4x 4y 1 0.
3.	4xy 4x 4y 0.								19.	3x2 3y2	4xy 6x 4y 7 0.
4.	2x2			2y2				2xy 6x 6y 3 0.	20.	4xy 4x 4y 6 0.
5.	3x2			3y2				4xy 6x 4y 2 0.	21.	5x2 5y2	2xy 10x 2y 1 0.
6.	2xy 2x 2y 1 0.								22.	2x2 2y2	4xy 8x 8y 1 0.
7.	x2 y2 4xy 4x 2y 2 0.								23.	x2 y2 2xy 2x 2y 1 0.
8.	4x2			4y2				2xy 10x 10y 1 0.	24.	2x2 2y2	4xy 8x 8y 1 0.
9.	4xy 4x 4y 2 0.								25.	3x2 3y2	2xy 12x 4y 1 0.
10.		x2	y2		2xy 8x 8y 1 0.				26.	4xy 8x 8y 1 0.
11.		x2	y2		4xy 8x 4y 1 0.				27.	2x2 2y2	2xy 6x 6y 6 0.
12.		x2	y2		2xy 2x 2y 7 0.				28.	x2 y2 4xy 4x 2y 5 0.
13.		2xy 2x 2y 3 0.							29.	4xy 4x 4y 4 0.
14.		4x2 4y2					2xy 12x 12y 1 0.		30.	3x2 3y2	4xy 4x 4y 1 0.
15.		3x2 3y2					4xy 8x 12y 1 0.		31.	x2 y2 4xy 4x 2y 1 0.
16.		x2	y2		8xy 20x 20y 1 0.

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

Задача 1. Доказать, что lim an a (указать N ( ) ).

a		1 2n2		, a	1	,
	n	2	4n2		2


0 .

	a	n	a			1 2n2						1	,
						1 2n2						1
						2 4n2						2
						2 4n2						2
	2 4n2 2 4n2										,
	2 4n2 2 4n2
			2(2 4n2 )
			2(2 4n2 )
			4				,

	2(2 4n2 )

n				1				1	,
n				2				2	,
				2				2
N ( )					1					1
N ( )
					2
					2					2

при n N( ) выполняется неравенство	a	n	a	, следовательно lim	1	2n2	1	.

						4n2	2
				n 2

Задача 2. Вычислить пределы числовых последовательностей.

lim

(6 n)2

lim

(36 12n n2 ) (36 12n n2 )

lim

24n

n)2

(1 n)2

(36 12n n2 ) (1 2n n2 )

n 14n

lim

n 14 35 / n

Задача 3. Вычислить пределы числовых последовательностей.

lim

n2 1 7n3

lim

n9 7

n 4 n12 n 1 n

4 1

n11

n12

Задача 4. Вычислить пределы числовых последовательностей.

n2 1

n2 1)(

n2 1

lim n(

1) lim

lim

n(n2 1 n2 1)

lim

1 1/ n

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

Задача 5. Вычислить пределы числовых последовательностей.

lim

(2n 1)! (2n 2)!

lim

1 (2n 2)

n (2n 3)! (2n 2)!

n (2n 2)(2n 3) (2n 2)

lim

2n 3

lim

n 4n2 8n 4

Задача 6. Вычислить пределы числовых последовательностей.

2n 3 n 1

2 n 1

2n 1

(n 1)

2n 1

lim

lim 1

2n 1

lim	2n 2	lim	2 2	/ n
en 2n 1		en 2 1/ n			e.

Задача 7 . Доказать (найти ( ) ), что lim

7x2 8x 1

x 1

7x 2

8x 1

x 1

7x 2

8x 1

7x 1 6

x 1

/ 7.

При 0 ( ) / 7.Это значит, что при x 1 функция имеет пределом число 6 .

Задача 8 . Доказать, что функция f (x) непрерывна в точке x0 (найти ( ) ).

f (x) 2x2 4, x		0	3.

f (x) f (x0	при			x x0	( ) ,

2x2 4 (2 9 4) 2x2 18 2 x2 9 ,

x2 9

/ 2,

(x 3)(x 3)

/ 2

x 3

/ 2

f (x) f (x0 )

выполняется при

x x0

( ) / 2.

Задача 9 . Вычислить пределы функций.

	(x2	2x 3)2	0		(x 1)2 (x 3)2		(x 1)2	(x 3)
lim				lim		lim			0.
	x3	4x2 3x			x(x 1)(x 3)			1)
x 3			0	x 3		x 3	x(x

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

Задача 10 . Вычислить пределы функций.

x 2

x 2)(4

x 2)

x 4

lim

x 16

x 4

x 16 (

x 4)(4

x 2)

x 16 (

x 4)(4

x 2)

lim

4 x

x 16

Задача 11 . Вычислить пределы функций.

ln(1 3x)

1 3x

lim

x 0

8x 4

2 x

1 1

2 x 0

2x 1

lim

2x 1

1 3x

2 x 0

2 1

Задача 12 . Вычислить пределы функций.

x2 1

x 1 y

( y 1)2

y 2 2 y

lim

y 0

lim

lim( y 2)

ln( y 1)

x 1

ln x

y 0

Задача 13 . Вычислить пределы функций.

tgx tg 2

2 x y

tg (2 y) tg

tg (2 y) tg 2

lim

y 0

lim

sin ln(x 1)

sin ln(1 y)

ln(1 y)

x 2

y 0

lim	1 cos 2	(2 y)	lim	1 y	1		1 tg 2	2.
	1 (1	y)		cos 2 (2 y)	cos 2	2
y 0			y 0

Задача 14 . Вычислить пределы функций.

	73x 32 x	0		(73x 1) (32 x 1)		3x ln 7 2x ln 3
lim			lim		lim		0.
	tgx x3			x x3		x2 1
x 0		0	x 0		x 0

Задача 15. Вычислить пределы функций.

	1 x2	0		2x	2	2	2
lim			lim					.
	sin x			cos x	cos
x 1		0	x 1

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

Задача 16. Вычислить пределы функций.

)

lim(cos

x ) x 1 lim(1 2 sin 2

x 0

1 .

x 0 2 x

lim

2 sin

2 sin2

lim

x 0

Задача 17. Вычислить пределы функций.

sin 2x

2x x2

lim

x 0 sin 3x

x 0

Задача 18. Вычислить пределы функций.

x 1

2x 1

1/(

x 1)

x 1 1/(

x 1)

x 1

lim

1 lim 1

lim 1

x 1 x

x 1

( x 1)( 3 x2

x 1

lim

( x 1)(

x 1)

lim

x 1

e x 1x(3 x 1)

e x 1 x(3 x 1)( 3 x2 3 x 1)

e x 1

x( x 1)

e x 1

e3 .

Задача 19. Вычислить пределы функций.

lim(sin x)3 /(1 x) (sin 2)1 sin 2.

x 2

Задача 20. Вычислить предел функции или числовой последовательности.

lim

2n sin n

lim

2 sin n / n

n 3 n3 7

n / n 3 n3 7 / n

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

Задача 1. Исходя из определения производной, найти f ' (0) .
		3	), x 0;
f (x)	sin(x sin
	sin(x sin
		x
	0, x 0.

x sin

sin x sin

sin

f (0) lim

lim

x sin x

lim sin

x 0

x sin

x 0

x sin

x 0

Задача 2. Составить уравнение нормали (в вариантах 1-12) или уравнение касательной (в вариантах 13-31) к

данной кривой в точке с абсциссой x0 .

y x x3 , x0 1 y 1 3x 2 ,

y(x0 ) 0, y (x0 ) 2,

y y(x0 )	1	(x x0 ) -уравнение нормали,

	y (x0 )
	y (x0 )

y 12 (x 1), y 12 x 12 .

Задача 3. Найти дифференциал dy .


y tg(2arccos				1 2x2 ), x 0.
			1				2			4x
dy			1				2			4x			dx


	2				1 x	2	1 (1 2x	2	2 1			2
cos		(2 arccos			1 x		1 (1 2x		2 1		2x

dx.

cos 2 (2 arccos 1

2x 2 )

2x 2

1 2x 2

2 cos 2 (2 arccos 1 2x 2 )

1 2x 2

Задача 4. Вычислить приближенно с помощью дифференциала.

y 3 x , x 1,21.

Выберем x0 1, следовательно x 0,21.

y(x) y(x0 x) y(x0 ) y (x0 ) x.

y	1		,


		x 2
33

y(x0 ) 1,

При необходимости более детального просмотра увеличьте масштаб документа! www.otlichka.ru

y (x0 ) 13 ,

y 1 13 0,21 1,07.

Задача 5. Найти производную.

y		x2		.


2	1		3x4

														12x3			x2
			2x		1 3x4									12x3			x2							4x(1 3x4 ) 12x5													4x 12x5 12x5

y	1													2 1 3x4							1													1													x
	1													2 1 3x4							1													1													x
																																																	.
	2									1 3x4												2												2
	2									1 3x4												2			2 (1 3x4 )3									2				2 (1 3x4 )3								(1 3x4 )3
Задача 6. Найти производную.
y x			1					ln(1 ex ).


		1 ex
y 1				0 e x									e x		1					e x							e x	.
y 1			(1 e x )2								1 e x				1					e x )2						1 e x		.
			(1 e x )2								1 e x						(1			e x )2						1 e x
Задача 7. Найти производную.
y ln3 (1 cos x)
y 3ln 2 (1 cos x)													sin x						3sin x ln 2 (1 cos x)												.
y 3ln 2 (1 cos x)																							1 cos x								.
											1			cos x									1 cos x
Задача 8. Найти производную.
y ctg (cos 5)										1		cos2 20x				.
y ctg (cos 5)																.
									40			sin 40x
y 0				1		2 20 cos 2x( sin 20x) sin 40x 40 cos 2 20x cos 40x
y 0			40																	sin 2 40x
			40																	sin 2 40x
	1			40 cos 20x sin 20x sin 40x 40 cos 2 20x cos 40x																														sin 2 40x 2 cos 2 20x cos 40x														.
																	sin 2																							2sin 2 40x								.
40																	sin 2			40																				2sin 2 40x
Задача 9. Найти производную.

y arctg					1 x2 1								.
y arctg								x					.
								x
															x		2
															x		2					1 x 2					1

																																x 2								x 2	(1 x 2 ) 1 x 2
y							1								1 x 2
							1								1 x 2

																				x	2
				( 1 x					2		1)		2								2							x	2	( 1			x		2	1)			2		x	2	1	x	2


	1
	1							x 2
								x 2
				1					1 x 2									.
																		.

1 x 2 (x 2 ( 1 x 2 1)2

<<< < Предыдущая 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1819 / 2719 20 21 22 23 24 25 26 27 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.03.2025121.29 Кб05ballov-75211.rtf
#
05.08.2019164.54 Кб96-16.docx
#
01.05.202566.61 Кб06. Экономическая часть.docx
#
23.09.201942.43 Кб660-82.docx
#
01.04.202599.33 Кб161-66_2novoe.doc
#
16.05.20157.64 Mб29626266.pdf
#
25.09.2019240.63 Кб1364-70, 115.docx
#
22.09.2019604.67 Кб1566-100.doc
#
01.04.2025573.66 Кб166-73.docx
#
23.09.201979.32 Кб137-12.docx
#
01.07.202584.99 Кб07-Нормир. нов.doc

4			2		1

1.	1		3		1 .
	1		2		2
	1		2		2
2			1		0
	1
2.	1		2		0	.
	1		1		1
	1		1		1
3			1	1

3.	0		2	1 .
	0		1	2
	0		1	2
5			1	1

4.	0		4	1 .
	0		1	4
	0		1	4
6			2		1

5.	1		5		1 .
	1		2		4
	1		2		4
3			1	1

6.		2	2	1 .
	2		1	4
	2		1	4
2			0	1

7.	1		1	1 .
	1		0	2
	1		0	2
2			1	0
	1
8.	1		2	0	.
	1		1	3
	1		1	3
4			1	0

9.	1		4	0	.
	1		1	5
	1		1	5
	5		1		1

10.		2	4		1 .
		2 1			6
		2 1			6
	5		4		4

11.		2	1		2	.
		2	0		3
		2	0		3

3		2		2
		1
12.	2	1		2	.
	2	2		3
	2	2		3
3		2		2

13.	0	3		0	.
	0	2		1
	0	2		1
5		2		2

14.	0	5		0	.
	0	2		3
	0	2		3
7		4		4

15.	2	3		2	.
	2	0		5
	2	0		5
7		6		6
		1
16.	4	1		4	.
	4	2		5
	4	2		5
7		6		6

17.	2	3		2	.
	2	2		3
	2	2		3
13		2		2
				6
18.	6	9		6			.
	2	2			5
	2	2			5
7		2	2
			2
19.	4	5	2		.
	0	0		3
	0	0		3
9		0		0
				4
20.	2	7		4		.
	2	2		5
	2	2		5
15		0			0
				4
21.	2	13		4			.
	2	2			11
	2	2			11
19		2		2
				6
22.	6	15		6			.
	2	2			11
	2	2			11

4		1		1

23.	2	3			2	.
	1	1		2
	1	1		2
2		1	1

24.	1	2	1 .
	0	0		1
	0	0		1
3		0		0

25.	1	2			1 .
	1	1
	1	1		2
5		0		0

26.	1	4			1 .
	1	1
	1	1		4
6		1		1

27.	2	5			2	.
	1	1		4
	1	1		4
9		6			6

28.	2		5		2 .
	2		2
	2		2		13
5		2			4

29.	0		3			0	.
	2		2			7
	2		2			7
7		4			2
	2				2
30.	2		5		2		.
	0		0			9
	0		0			9
	4	3		3

31.	1	2		1	.
	1	1		2
	1	1		2

4			2		1

1.	1		3		1 .
	1		2		2
	1		2		2
2			1		0
	1
2.	1		2		0	.
	1		1		1
	1		1		1
3			1	1

3.	0		2	1 .
	0		1	2
	0		1	2
5			1	1

4.	0		4	1 .
	0		1	4
	0		1	4
6			2		1

5.	1		5		1 .
	1		2		4
	1		2		4
3			1	1

6.		2	2	1 .
	2		1	4
	2		1	4
2			0	1

7.	1		1	1 .
	1		0	2
	1		0	2
2			1	0
	1
8.	1		2	0	.
	1		1	3
	1		1	3
4			1	0

9.	1		4	0	.
	1		1	5
	1		1	5
	5		1		1

10.		2	4		1 .
		2 1			6
		2 1			6
	5		4		4

11.		2	1		2	.
		2	0		3
		2	0		3

3		2		2
		1
12.	2	1		2	.
	2	2		3
	2	2		3
3		2		2

13.	0	3		0	.
	0	2		1
	0	2		1
5		2		2

14.	0	5		0	.
	0	2		3
	0	2		3
7		4		4

15.	2	3		2	.
	2	0		5
	2	0		5
7		6		6
		1
16.	4	1		4	.
	4	2		5
	4	2		5
7		6		6

17.	2	3		2	.
	2	2		3
	2	2		3
13		2		2
				6
18.	6	9		6			.
	2	2			5
	2	2			5
7		2	2
			2
19.	4	5	2		.
	0	0		3
	0	0		3
9		0		0
				4
20.	2	7		4		.
	2	2		5
	2	2		5
15		0			0
				4
21.	2	13		4			.
	2	2			11
	2	2			11
19		2		2
				6
22.	6	15		6			.
	2	2			11
	2	2			11

4		1		1

23.	2	3			2	.
	1	1		2
	1	1		2
2		1	1

24.	1	2	1 .
	0	0		1
	0	0		1
3		0		0

25.	1	2			1 .
	1	1
	1	1		2
5		0		0

26.	1	4			1 .
	1	1
	1	1		4
6		1		1

27.	2	5			2	.
	1	1		4
	1	1		4
9		6			6

28.	2		5		2 .
	2		2
	2		2		13
5		2			4

29.	0		3			0	.
	2		2			7
	2		2			7
7		4			2
	2				2
30.	2		5		2		.
	0		0			9
	0		0			9
	4	3		3

31.	1	2		1	.
	1	1		2
	1	1		2

4			2		1

1.	1		3		1 .
	1		2		2
	1		2		2
2			1		0
	1
2.	1		2		0	.
	1		1		1
	1		1		1
3			1	1

3.	0		2	1 .
	0		1	2
	0		1	2
5			1	1

4.	0		4	1 .
	0		1	4
	0		1	4
6			2		1

5.	1		5		1 .
	1		2		4
	1		2		4
3			1	1

6.		2	2	1 .
	2		1	4
	2		1	4
2			0	1

7.	1		1	1 .
	1		0	2
	1		0	2
2			1	0
	1
8.	1		2	0	.
	1		1	3
	1		1	3
4			1	0

9.	1		4	0	.
	1		1	5
	1		1	5
	5		1		1

10.		2	4		1 .
		2 1			6
		2 1			6
	5		4		4

11.		2	1		2	.
		2	0		3
		2	0		3

3		2		2
		1
12.	2	1		2	.
	2	2		3
	2	2		3
3		2		2

13.	0	3		0	.
	0	2		1
	0	2		1
5		2		2

14.	0	5		0	.
	0	2		3
	0	2		3
7		4		4

15.	2	3		2	.
	2	0		5
	2	0		5
7		6		6
		1
16.	4	1		4	.
	4	2		5
	4	2		5
7		6		6

17.	2	3		2	.
	2	2		3
	2	2		3
13		2		2
				6
18.	6	9		6			.
	2	2			5
	2	2			5
7		2	2
			2
19.	4	5	2		.
	0	0		3
	0	0		3
9		0		0
				4
20.	2	7		4		.
	2	2		5
	2	2		5
15		0			0
				4
21.	2	13		4			.
	2	2			11
	2	2			11
19		2		2
				6
22.	6	15		6			.
	2	2			11
	2	2			11

4		1		1

23.	2	3			2	.
	1	1		2
	1	1		2
2		1	1

24.	1	2	1 .
	0	0		1
	0	0		1
3		0		0

25.	1	2			1 .
	1	1
	1	1		2
5		0		0

26.	1	4			1 .
	1	1
	1	1		4
6		1		1

27.	2	5			2	.
	1	1		4
	1	1		4
9		6			6

28.	2		5		2 .
	2		2
	2		2		13
5		2			4

29.	0		3			0	.
	2		2			7
	2		2			7
7		4			2
	2				2
30.	2		5		2		.
	0		0			9
	0		0			9
	4	3		3

31.	1	2		1	.
	1	1		2
	1	1		2