
Ekzamen_fizika
.pdf
Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению (см. §2.1):
F (t) = ma (t) = –m ω2 x (t).
В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука: Fупр = –kx.
Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором.
Круговая частота ω0 свободных колебаний груза на пружине находится из второго закона Ньютона:
откуда
Частота ω0 называется собственной частотой колебательной системы.
Период T гармонических колебаний груза на пружине равен
При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину x0,
равную 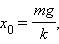
и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты ω0 и периода колебаний Tсправедливы и в этом случае.
Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела a и координатойx: ускорение является второй производной координаты тела x по времени t:
Поэтому второй закон Ньютона для груза на пружине может быть записан в виде 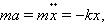
или 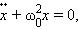 где
где
5. атематическиймаятник — осциллятор, представляющий собой механическую систему, состоящую изматериальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника
длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит от амплитуды колебаний и массы маятника.

Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
где 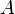 — амплитуда колебаний маятника,
— амплитуда колебаний маятника, 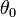 — начальная фаза колебаний,
— начальная фаза колебаний,  — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями
— циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями
6. Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим. Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс C физического маятника находится ниже оси вращения O на
вертикали, проходящей через ось. При отклонении маятника на угол φ возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:M = –(mg sin φ)d.
Здесь d – расстояние между осью вращения и центром масс C.
Знак «минус» в этой формуле, как обычно, означает, что момент сил стремится повернуть маятник в направлении, противоположном его отклонению из положения равновесия. Как и в случае математического маятника, возвращающий момент M пропорционален sin φ. Это означает, что только при малых углах φ, когда sin φ ≈ φ, физический маятник способен совершать свободные гармонические колебания. В случае малых колебанийM = –mgdφ.
и второй закон Ньютона для физического маятника принимает вид Iε = M = –mgdφ.
где ε – угловое ускорение маятника, I – момент инерции маятника относительно оси вращения O. Модуль коэффициента пропорциональности между ускорением и смещением равен квадрату круговой частоты:
Здесь ω0 – собственная частота малых колебаний физического маятника. Следовательно,
Окончательно для круговой частоты ω0 свободных колебаний физического маятника получается
выражение:
7.В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур.
Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде
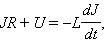 где
где 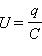 – напряжение на конденсаторе, q – заряд конденсатора,
– напряжение на конденсаторе, q – заряд конденсатора, 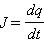 – ток в цепи. В правой части этого соотношения стоит ЭДС самоиндукции катушки.
– ток в цепи. В правой части этого соотношения стоит ЭДС самоиндукции катушки.
Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда

Здесь принято обозначение: |
|
|
Уравнение (*) описывает свободные колебания |
||||||||||
в LC-контуре в отсутствие затухания. По виду оно в точности совпадает с уравнением свободных |
|||||||||||||
колебаний груза на пружине в отсутствие сил трения. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Электрические величины |
|
|
Механические величины |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заряд конденсатора |
|
|
q (t) |
|
Координата |
|
|
x (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ток в цепи |
|
|
|
|
|
Скорость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Индуктивность |
|
|
L |
|
|
Масса |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Величина, обратная |
|
|
|
|
|
Жесткость |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
электроемкости |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Напряжение на |
|
|
|
|
|
Упругая сила |
|
|
kx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
конденсаторе |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Энергия |
|
|
|
|
|
Потенциальная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
электрического поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
энергия пружины |
|
|
|
|
|
|
|
|
конденсатора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Магнитная энергия |
|
|
|
|
|
Кинетическая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
катушки |
|
|
|
|
|
энергия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Магнитный поток |
|
|
LI |
|
|
Импульс |
|
|
mυ |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону q(t) = q0 cos(ωt + φ0).
Параметры L и C колебательного контура определяют только собственную частоту свободных
колебаний
Амплитуда q0 и начальная фаза φ0 определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. В частности, для процесса колебаний, который начнется в контуре (рис. 2.2.1) после переключения ключа K в положение
2, q0 = C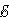 , φ0 = 0.
, φ0 = 0.
При свободных колебаниях происходит периодическое превращение электрической энергии Wэ, запасенной в конденсаторе, в магнитную энергию Wм катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:
Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими.

8.Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно
длящийся процесс вида 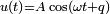 в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной
в природе невозможен. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний A является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной
зависимостью от скорости колебаний 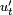 или её квадрата.
или её квадрата.
Дифференциальное уравнение свободных затухающих колебаний записывается в виде: (дS2)/(дt2)+2δ(ds/dt)+ω02s=0, где
s- колеблющаяся величина, описывающая тот или иной физический процесс, δ=constкоэффициент затухания, ω0- циклическая частота свободных незатухающих колебаний той же колебательной системы, при δ=0, называется собственной частотой колебательной системы. Решение уравнения рассмотрим в виде: s=e-δtu, где u=u(t), после нахождения первой и второй производной получим ˙u˙+(ω02- δ2)u=0. Решение уравнения зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положительный: ω2=ω02- δ2, если (ω02- δ2)>0, тогда получим уравнение ˙u˙+ω2u=0, решением которого является функция u=A0cos(ωt+φ). Таким образом решение
дифференциального уравнения в случае малых затуханий s=A0e-δtcos(ωt+φ), где А= A0e-δt — амплитуда затухающих колебаний.
9. Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:
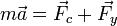 где
где 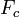 — сила сопротивления,
— сила сопротивления, 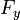 — сила упругости
— сила упругости
, 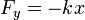 , то есть
, то есть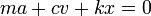
или в дифференциальной форме
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения: 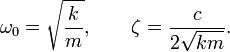
Величину 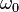 называют собственной частотой системы,
называют собственной частотой системы, 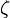 — коэффициентом затухания.
— коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
или
Сделав замену 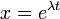 , получают характеристическое уравнение
, получают характеристическое уравнение
Корни которого вычисляются по следующей формуле
10. Время релаксации
Промежуток времени τ, за который амплитуда уменьшается в «е» раз, называется временем затухания (или релаксации), где «е» – основание натурального логарифма, е ≈ 2,718.
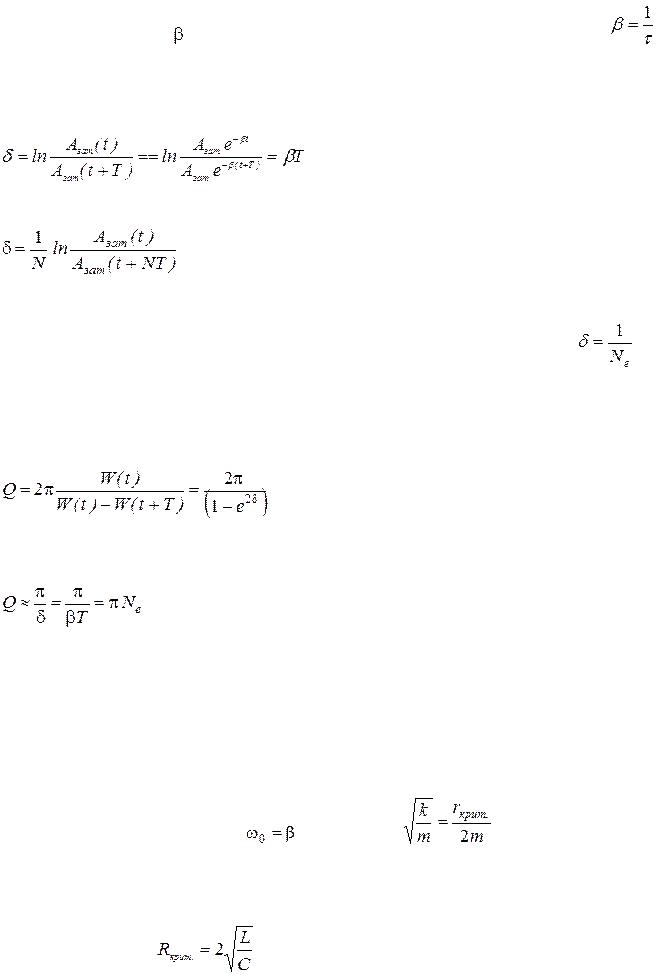
оэффициент затухания – величина, обратно пропорциональная времени релаксации |
. |
Логарифмический декремент затухания 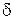 – физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период:
– физическая величина, численно равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих по времени на период:
.
Если затухание колебаний мало, то логарифмический декремент рассчитывается по формуле:
, где Азат.(t) и Азат.(t+NT) – соответственно амплитуды колебаний в момент времени t и через N периодов, т.е. в момент времени (t + NT).
Если взять число колебаний Ne, за которое амплитуда уменьшается в «е» раз, тогда |
. |
Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) на отношение энергииW(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:
.
При малых значениях логарифмического декремента δ можно рассчитывать по формуле:
При увеличении коэффициента 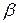 частота затухающих колебаний уменьшается, а период
частота затухающих колебаний уменьшается, а период
увеличивается. При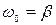 частота затухающих колебаний становится равной нулю ωзат. = 0, а период колебаний Тзат. = ∞, и колебания теряют периодический характер, они называются
частота затухающих колебаний становится равной нулю ωзат. = 0, а период колебаний Тзат. = ∞, и колебания теряют периодический характер, они называются
апериодическими. При 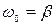 параметры системы, ответственные за убывание колебательной энергии, принимают значения, называемые критическими.
параметры системы, ответственные за убывание колебательной энергии, принимают значения, называемые критическими.
Для пружинного маятника условие |
соответствует |
, отсюда величин |
критического коэффициента сопротивления равна: 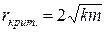 .
.
Для LCR – контура критическое сопротивление контура, при котором колебания потеряют свою
периодичность равно: |
. |

11. Под сложением колебаний понимают нахождение закона результирующих колебаний системы в тех случаях, когда эта система одновременно участвует в нескольких колебательных процессах. Различают два предельных случая – сложение колебаний одинакового направления и сложение взаимно перпендикулярных колебаний.
На практике (например, в электротехнике) часто приходится иметь дело с колебаниями одинаковой частоты. Любые два таких колебания можно представить в виде: y1 =
A1 sin (ωt + φ1) ; y2 = A2 sin (ωt + φ2) .
Особый интерес представляет случай, когда начальная фаза первого колебания равна 0, а
начальная фаза |
второго колебания равна π/2. |
|
|||||
Тогда y1 = A1 sin ωt ; |
y2 = A2 sin (ωt + π/2) . Сумма таких гармонических колебаний |
||||||
равна: A |
1 |
sin ωt |
+ A |
2 |
cos ωt = \/A |
2 + A 2 • sin (ωt + φ). |
(1) где |
|
|
|
1 |
2 |
|
||
угол φ определяется из условий
|
(2) |
|
Формула (1) показывает, что если два гармонических колебания имеют |
одинаковую |
|
частоту и фазы 0 и π/ , то их сумма есть гармоническое колебание той же |
||
2 |
|
|
частоты. |
|
|
Амплитуда А суммарного колебания выражается через амплитуды A1и A2 |
слагаемых |
|
колебаний по формуле A = \/A 2 |
+ A 2, а начальная фаза φ определяется из условий. |
|
1 |
2 |
|
12. БИЕНИЯ - периодич. изменения во времени амплитуды колебания, возникающего при сложении двух гармонических колебаний с близкими частотами. Б. появляются вследствие того, что величина разности фаз между двумя колебаниями с разл. частотами всё время изменяется так, что оба колебания оказываются в какой-то момент времени в фазе, через нек-рое время в противофазе, затем снова в фазе и т. д. Соответственно амплитуда результирующего колебания периодически достигает то максимума, равного сумме амплитуд складываемых колебаний, то минимума, равного разности этих амплитуд (рис.). Напр., Б. возникают при звучании двух камертонов с близкими частотами - звук поочерёдно усиливается и ослабевает, при сложении нормальных колебаний с близкими частотами в связанных линейных осцилляторах.
При сложении двух бегущих в одном направлении волн с близкими частотами и волновыми числами Б. возникают не только во времени, но и в пространстве. Складывая, напр., волны с равными амплитудами
получаем результирующую волну
с частотой 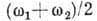 и волновым числом
и волновым числом 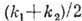 , к-рыеблизки к частоте и волновому числу любой из компонент. Амплитуда волны модулирована в пространстве и времени
, к-рыеблизки к частоте и волновому числу любой из компонент. Амплитуда волны модулирована в пространстве и времени
медленно меняющейся огибающей с частотой 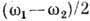 и волновым числом
и волновым числом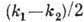 . Частота Б. равна разности частот складываемых компонент
. Частота Б. равна разности частот складываемых компонент 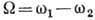 .
.
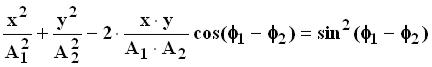
13. Рассмотрим два векторных колебания, описываемых уравнениями:
r1 = A1·cos(w1·t + 1);
r2 = A2·cos(w2·t + 2).
Заметим, что с течением времени направление векторов не изменяется, а изменяется только их амплитуда. Очевидно также, что вектор A1параллелен r1, а
вектор A2 параллелен r2. Задача: найти r = r1 + r2. Рассмотрим только случай взаимноперпендикулярных колебаний (см. рис. 11.9 ).
Вдоль вектора r1 направим ось Х, вдоль r2 - ось Y. Очевидно, результирующий вектор r перемещается в плоскости XY. ривая, описываемая концом вектора r, называется фигурой Лиссажу. Эта фигура вписывается в четырехугольник со сторонами 2·A1 и 2·A2, а ее вид зависит от соотношения частот, фаз и амплитуд складываемых колебаний.
Рассмотрим случай синхронных взаимно-перпендикулярных колебаний:
r1 |
= A1·cos (w·t + 1); |
(11.7) |
r2 |
= A2·cos (w·t + ). |
(11.8) |
Спроецировав уравнения (11.7) и (11.8) на оси координат и проведя суммирование проекций, получим:
x = A1·cos (w·t + 1); |
(11.9) |
y = A2·cos (w·t + ). |
(11.10) |
Исключив с помощью тригонометрических преобразований t из (11.9) и (11.10), получим математическое выражение фигуры Лиссажу, которое представляет собой уравнение эллипса:
. (11.11)
Вид эллипса определяется величиной сдвига фаз . В общем случае, когда отлична от 0, полуоси эллипса повернуты относительно осей X и Y.
Если сдвиг фаз = 0, то как следует из уравнения (11.11) будет справедливо следующее выражение:
(х/А1 - y/A2)2 = 0 или y = А2·x/А1.
Т.е. фигура Лиссажу представляет из себя прямую линию с углом наклона к оси X (tg = А2/А1). Если = , то y = - А2·x/А1.
Если = , то имеем классическое уравнение эллипса, полуоси которого параллельны осям координат:
х2/А12 + y2/A22 = 1.
Если = и А1 = А2 = A, то эллипс превращается в окружность радиуса A.
14.Рассмотрим случай сложения несинхронных взаимно перпендикулярных колебаний. Пусть w1 не равняется w2, но частоты исходных колебаний относятся как целые
числа: w1/w2 = n1/n2. Рассмотрим следующий пример:
x= A1·sin w·t;
y= A2·sin (2·w·t).
Для нахождения вида фигуры Лиссажу используем метод графического исключения t. Изобразим на одном графике зависимости x(t) и y(t). Отметим на этом графике положение точек в некоторые последовательные моменты времени. Затем перенесем эти точки на плоскость XY. В результате получим фигуру Лиссажу типа восьмерки (см. рис. 11.10). Если взять колебания с разными начальными фазами, то при таком же соотношении частот также получим фигуры Лиссажу типа восьмерки, но не симметричные относительно осей координат. При = , фигура Лиссажу примет вид параболы (см. рис. 11.11).
Существует правило частот Лиссажу, по которому можно определить отношение частот складываемых колебаний. Об этом судят по числу точек пересечения фигуры прямыми, параллельными осям координат:
wy/wx = nx/ny.
Откуда это следует? Обозначим за - минимальное время, в течение которого полностью описывается фигура Лиссажу. Очевидно, что равно наименьшему кратному периодов колебаний Tx и Ty, совершающихся вдоль осей X и Y. За один период конец вектора r пересечет ось X 2 раза. Следовательно, за время число пересечений этой оси будет равно nx = 2· /Ty. Аналогично ny = 2· /Tx. Следовательно, ny/nx = Ty/Tx = wx/wy.
Метод фигур Лиссажу широко используется для определения соотношения частот и фаз складываемых колебаний (например, в радиотехнике для градуировки генераторов). Чувствительность фигуры Лиссажу к разности фаз используется для исследования фазовых соотношений в цепях переменного тока.
