
Ekzamen_fizika
.pdf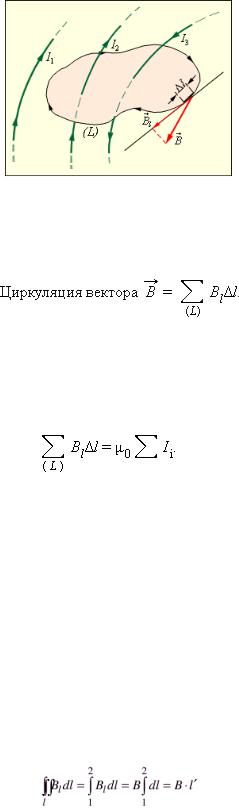
Изображены токи I1, I2 и I3, создающие магнитное поле.
Циркуляцией вектора 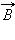 называют сумму произведений
называют сумму произведений 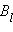 Δl, взятую по всему контуру L:
Δl, взятую по всему контуру L:
Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур L в то время, как другие токи могут находиться в стороне от контура. Теорема о циркуляции утверждает, что циркуляция
вектора 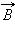 магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0 на сумму всех токов, пронизывающих контур:
магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0 на сумму всех токов, пронизывающих контур:
15. Магнитную индукцию поля бесконечно длинного соленоида можно вы числить, используя закон полного тока. Соленоид представляет собой тонкий провод, навитый плотно виток к витку на цилиндрический каркас. Он эквивалентен системе одинаковых круговых токов с общей прямой осью. Бесконечно длинный соленоид симметричен относительно любой перпендикулярной его оси плоскости. В любой точке внутри и вне соленоида вектор B может иметь лишь направление параллельное оси. Возьмем прямоугольный контур.Циркуляцию B по этому контуру можно представить следующим образом:
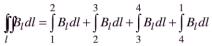 .
.
Второй и четвертый интегралы равны нулю, так как вектор B перпендикулярен к участкам контура, по которым они берутся. Для участка 3–4 на большом расстоянии от соленоида поле должно быть очень слабым, поэтому третьим слагаемым можно пренебречь. Тогда:
где B –магнитная индукция в тех точках, где располагается отрезок 1-2, l –длина этого отрезка.
Если отрезок проходит внутри соленоида на любом расстоянии от его оси контур охватывает суммарный ток nlI , где n – число витков соленоида, приходящееся на единицу длины, I – сила тока соленоида. Поэтому
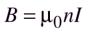 (3)
(3)
Если отрезок 1 – 2 располагается вне соленоида, то охватываемый контуром ток равен нулю .Таким образом, вне бесконечно длинного соленоида магнитная индукция равна нулю, внутри – всюду

одинакова и имеет величину определяемую формулой (3), т.е. магнитное поле внутри соленоида является однородным.
В магнитную индукцию на оси соленоида симметрично расположенные витки вносят одинаковый вклад. Поэтому, у конца полу бесконечного соленоида на его оси магнитная индукция равна
половине значения (3), т.е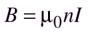 :2
:2
Практически, если длина соленоида значительно больше, чем его диаметр, формула (3) будет справедлива для точек в средней части соленоида, а формула (4) – для точек на оси вблизи его концов.
16.
Действие магнитного поля на проводник с током
Сила, действующая на проводник с током в магнитном поле,
называется силой Ампера.
Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:
F=B.I.ℓ. sin α — закон Ампера.
Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током.
Сила 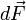 , с которой магнитное поле действует на элемент
, с которой магнитное поле действует на элемент 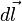 проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока
проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока 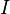 в проводнике и векторному произведению элемента длины
в проводнике и векторному произведению элемента длины 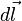 проводника на магнитную индукцию
проводника на магнитную индукцию 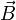 :
: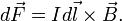
17. равне нияМа ксвелла— система дифференциальных уравнений, описывающих электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах. Вместе с выражением для силы Лоренца образуют полную систему уравнений классической электродинамики. равнения, сформулированные Джеймсом лерком Максвеллом на основе накопленных к середине XIX века экспериментальных результатов, сыграли ключевую роль в развитии представлений теоретической физики и оказали сильное, зачастую решающее, влияние не только на все области физики, непосредственно связанные с электромагнетизмом, но и на многие возникшие впоследствии фундаментальные теории, предмет которых не сводился к электромагнетизму.
Первое М. у. имеет вид:
Второе М. у. является математической формулировкой закона электромагнитной индукции Фарадея записывается в виде:
,
Третье М. у. выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим (магнитное поле порождается только токами):
Четвёртое М. у. (обычно называемое Гаусса теоремой) представляет собой обобщение закона взаимодействия неподвижных электрических зарядов — Кулона закона:
18. лектростатика — раздел учения об электричестве, изучающий взаимодействие неподвижных электрических зарядов. Между одноимённо заряженными телами возникает электростатическое (или кулоновское) отталкивание, а между разноимённо заряженными — электростатическое притяжение. Явление отталкивания одноименных зарядов лежит в основе создания электроскопа — прибора для обнаружения электрических зарядов.В основе электростатики лежит закон улона. тот закон описывает взаимодействие точечных электрических зарядов.
Максвелл явился истолкователем идей Фарадея. Он облек эти идеи в математическую форму. Основание теории Максвелла заключается не в законе Кулона, а в принятии гипотезы, которая выражается в следующем равенстве:
Электростатическое поле описывается системой дифференциальных уравнений, которая получается из системы уравнений Максвелла в предположении, что векторы поля не зависят от времени и отсутствует перемещение зарядов (j = 0). Аналогично находятся основные уравнения электростатики в интегральной форме:
Потенциал электростатического поля — скалярная
величина, равная отношению потенциальной энергии заряда
в поле к этому заряду: |
|
|
|
|
|
- |
энергетическая |
характеристика |
поля |
в |
данной |
точке. Потенциал не зависит от величины заряда, помещенного в это поле.
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной.
За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора.
- следствие принципа суперпозиции полей (потенциалы |
|||||
складываютсяалгебраически). |
|
|
|
|
|
Потенциал |
численно |
равен |
работе |
поля |
по |
перемещению единичного положительного заряда из данной |
|||||
точки электрического поля в бесконечность. |
|
|
|||
В СИ потенциал измеряется в вольтах: |
|
|
|
||
Разность потенциалов
Напряженность и потенциал – это две характеристики одного и того же объекта – электрического поля, поэтому между ними должна существовать функциональная связь. Действительно, работа сил поля по перемещению заряда q из одной точки пространства в другую может быть представлена двояким образом:
Откуда следует, что
Или
Это и есть искомая связь между напряженностью и потенциалом электрического поля в дифференциальном виде.
- вектор, направленный из точки с меньшим потенциалом в
точку с большим потенциалом (рис.2.11).
, 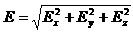 .
.
Рис.2.11. Векторы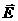 и gradφ. .
и gradφ. .
Из свойства потенциальности электростатического поля следует, что работа сил поля по замкнутому контуру (φ1= φ2) равна нулю:
,
поэтому можем написать
Последнее равенство отражает суть второй основной теоремыэлектростатики – теоремы о
циркуляции электрического поля, согласно которой циркуляция поля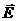 вдоль произвольного замкнутого контура равна нулю. Эта теорема является прямым следствием потенциальности электростатического поля.
вдоль произвольного замкнутого контура равна нулю. Эта теорема является прямым следствием потенциальности электростатического поля.
19. Магнитоста тика— раздел классической электродинамики, изучающий взаимодействие постоянных токов посредством создаваемого ими постоянного магнитного поля и способы расчета магнитного поля в этом случае.
Все основные уравнения магнитостатики линейны(как и классической электродинамики вообще, частным случаем которой магнитостатика является). Это подразумевает важную роль в магнитостатике (тоже как и во всей электродинамике) принципа суперпозиции.
Принцип суперпозиции для магнитостатики может быть сформулирован так: Магнитное поле,
создаваемое несколькими токами, есть векторная сумма полей, которые бы создавались каждым из этих токов по отдельности.
Этот принцип одинаково формулируется и, в принципе, одинаково используется для вектора магнитной индукции и для векторного потенциала и применяется при расчетах повсеместно. Особенно очевидным и прямым образом это проявляется, когда при применении закона Био—Савара (см. ниже) для расчета
магнитного поля 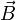 производится суммирование (интегрирование) бесконечно малых вкладов
производится суммирование (интегрирование) бесконечно малых вкладов 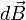 , создаваемых каждым бесконечно малым элементом тока, текущих в разных точках пространства (точно так же и при применении варианта этого закона для векторного потенциала).
, создаваемых каждым бесконечно малым элементом тока, текущих в разных точках пространства (точно так же и при применении варианта этого закона для векторного потенциала).
Основные уравнения, используемые в магнитостатике[2]:
Закон Био — Савара — Лапласа (величина магнитного поля, генерируемого в данной точке элементом тока)
;
Теорема о циркуляции магнитного поля
она же в дифференциальной форме:
Выражение для силы Лоренца (силы, с которой на движущуюся заряженную частицу действует магнитное поле)
Выражение для силы Ампера (силы, с которой на элемент тока действует магнитное поле)
Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил висточниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.
ЭДС можно выразить через напряжённость электрического поля сторонних сил (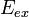 ). В замкнутом контуре (
). В замкнутом контуре ( 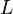 ) тогда ЭДС будет равна:
) тогда ЭДС будет равна:
, где 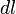 — элемент длины контура.
— элемент длины контура.
ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного

заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.
Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
где  — поток магнитного поля через замкнутую поверхность
— поток магнитного поля через замкнутую поверхность 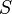 , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре.
, ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре.
20.Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре
при изменении магнитного потока, проходящего через него.Магнитным потоком Φ через
площадь S контура называют величину Ф=B*S*cosa.
Электромагнитная индукция была открыта Майклом Фарадеем в 1831 году. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре
возникает ЭДС индукции 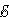 инд, равная скорости изменения магнитного потока через поверхность,
инд, равная скорости изменения магнитного потока через поверхность,
ограниченную контуром, взятой со знаком минус:
Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называетсяправилом Ленца.
Согласно закону электромагнитной индукции Фарадея (в СИ):
где
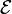 — электродвижущая сила, действующая вдоль произвольно выбранного контура,
— электродвижущая сила, действующая вдоль произвольно выбранного контура,
— магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает равило Ленца, названное так по имени русского физика Э. Х. Ленца:
Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что
создаваемое им магнитное поле противодействует тому изменению магнитного потока,
которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
Где 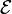 — электродвижущая сила,
— электродвижущая сила, 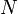 — число витков,
— число витков, 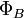 — магнитный поток через один виток,
— магнитный поток через один виток,
21. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение ток смещения. Этот термин имеет смысл в таких веществах, как, например, диэлектрики. Там смещаются заряды под действием электрического поля. Но в вакууме зарядов нет – там смещаться нечему, а магнитное поле есть. То есть название Максвелла «ток смещения» – не совсем удачное, но смысл, вкладываемый в него Максвеллом, – правильный.
Максвелл сделал вывод: всякое переменное электрическое поле порождает переменное магнитное поле.
Токи проводимости в проводнике замыкаются токами смещения в диэлектрике или в вакууме. Переменное электрическое поле в конденсаторе создает такое же магнитное поле, как если бы между обкладками существовал ток проводимости, имеющий величину, равную току в металлическом проводнике
Это утверждение позволяет (на базе нашего примера с конденсатором) найти величину тока смещения. В свое время мы с вами доказали, что поверхностная плотность поляризационных зарядов
σ равна 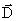 – вектору электрического смещения:
– вектору электрического смещения:
Полный заряд на поверхности диэлектрика и, следовательно, на обкладках конденсатора 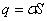 (S
(S
– площадь обкладки)
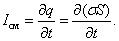 Тогда
Тогда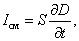
т.е. ток смещения пропорционален скорости изменения вектора электрического смещения 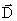 .
.
Поэтому он и получил такое название – ток смещения. Плотность тока смещения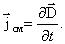
22.Введение аксвеллом онятия тока смещения ривело его к завершению созданной им единой
макроско ической теории электромагнитного оля, озволившей с единой точки зрения не только объяснить электрические и магнитные явления, но и редсказать новые, существование которых было в оследствии
одтверждено.
В основе теории аксвелла лежат рассмотренные выше четыре уравнения:
Первое М. у. имеет вид:
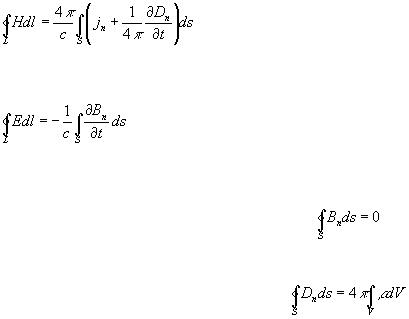
Второе М. у. является математической формулировкой закона электромагнитной индукции Фарадея записывается в виде:
,
Третье М. у. выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим (магнитное поле порождается только токами):
Четвёртое М. у. (обычно называемое Гаусса теоремой) представляет собой обобщение закона взаимодействия неподвижных электрических зарядов — Кулона закона:
з уравнения аксвелла вытекает, что источниками электрического оля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные оля, а магнитные оля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо еременными электрическим олями. Уравнения
аксвелла не симметричны относительно электрического и магнитного олей. Это связано с тем, что в рироде
существуют электрические заряды, но нет зарядов магнитных. |
|
Уравнения аксвелла - наиболее общие уравнения для электрических и магнитных олей в |
окоящихся средах. |
Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. |
з уравнений |
аксвелла следует, что еременное магнитное оле всегда связано с орождаемым им электрическим олем, а еременное электрическое оле всегда связано с орождаемым им магнитным, т. е. Электрическое и магнитное оля неразрывно связаны друг с другом – они образуют единое электромагнитное оле.
1. олебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.
олебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.
олебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны c волнами. Поэтому исследованиями этих закономерностей занимается обобщённая теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии.
Выделение разных видов колебаний зависит от подчёркиваемых свойств колеблющихся систем (осцилляторов)
По физической рироде
еханические (звук, вибрация)
Электромагнитные (свет, радиоволны, тепловые)
Смешанного ти а — комбинации вышеперечисленных
По характеру взаимодействия с окружающей средой
Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частотыосциллятора и частоты внешнего воздействия.
Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Простейшими
примерами свободных колебаний являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.
Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы —механические часы). Характерным отличием автоколебаний от свободных колебаний является, то что их амплитуда определяется свойствами самой системы, а не начальными условиями.
Параметрические — колебания, возникающие при изменении какого-либо параметра колебательной системы в результате внешнего воздействия.
Случайные — колебания, при которых внешняя или параметрическая нагрузка является случайным процессом.
Характеристики
Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы,  (м)
(м)
Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), 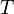 (с)
(с)
Частота — число колебаний в единицу времени, 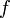 (Гц, с−1).
(Гц, с−1).
Период колебаний 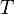 и частота
и частота 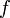 — обратные величины;
— обратные величины;
и
В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота  (рад/с, Гц, с−1), показывающая число колебаний за
(рад/с, Гц, с−1), показывающая число колебаний за 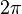 единиц времени:
единиц времени:
Смещение — отклонение тела от положения равновесия. Обозначение Х, Единица измерения метр.
Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы.
2.Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса.
Уравнение гармонических колебаний имеет вид:
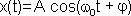 ,
,
где A - амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия); 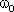 - круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса
- круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса 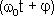 - называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t.
- называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t.
Постоянная φ представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета. Величина x может принимать значения, лежащие в пределах от -A до +A.
Промежуток времени T, через который повторяются определенные состояния колебательной системы, называется периодом колебаний. Косинус - периодическая функция с периодом 2π, поэтому за промежуток времени T, через который фаза колебаний получит приращение равное 2π, состояние системы, совершающей гармонические колебания, будет повторяться. Этот промежуток времени T называется периодом гармонических колебаний.
Период гармонических колебаний равен: T = 2π/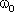 .
.
Число колебаний в единицу времени называется частотой колебаний ν.
Частота гармонических колебаний равна: ν = 1/T. Единица измерения частоты герц (Гц) - одно
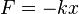
колебание в секунду.
Круговая частота 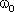 = 2π/T = 2πν дает число колебаний за 2π секунд.
= 2π/T = 2πν дает число колебаний за 2π секунд.
3.
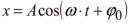 , (4.1)
, (4.1)
Скорость 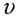 колеблющейся материальной точки получим, продифференцировав (4.1) по времени:
колеблющейся материальной точки получим, продифференцировав (4.1) по времени:
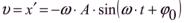 . (4.5)
. (4.5)
Продифференцировав (4.5), получим ускорение а:
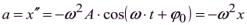 . (4.6)
. (4.6)
Или:
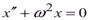 . (4.7)
. (4.7)
Выражение (4.7) описывает гармонические колебания величины x и называется дифференциальным уравнением гармонического осциллятора. Его решением является гармоническая функция (4.1). Если вторая производная по времени какой-либо физической величины (не обязательно смещения) пропорциональна самой величине с противоположным знаком, то данная физическая величина изменяется со временем по гармоническому закону.
армоническийосциллятор (в классической механике) — система, которая при смещении из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x (согласно закону
ука):
где k — коэффициент жёсткости системы.
Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.
Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.
Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.
Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы.
Простое гармоническое движение — это движение простого гармонического осциллятора, периодическое движение, которое не является ни вынужденным, низатухающим. Тело в простом гармоническом движении подвергается воздействию единственной переменной силы, которая по модулю прямо пропорциональна смещению x от положения равновесия и направлена в обратную сторону.
Это движение является периодическим: тело колеблется около положения равновесия по синусоидальному закону. Каждое последующее колебание такое же, как и
предыдущее, и период, частота и амплитуда колебаний остаются постоянными. Если принять, что положение равновесия находится в точке с координатой, равной нулю, то смещение x тела от положения равновесия в
любой момент времени даётся формулой: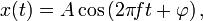
4.Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.
