
Ekzamen_fizika
.pdfВоснове закона сохранения импульса лежит однородность пространства, т. е. одинаковость свойств пространства во всех точках (симметрия по отношению к сдвигу начала координат). Одинаковость следует понимать в том смысле, что параллельный перенос замкнутой системы из одного места пространства в другое, без изменения взаимного расположения и скоростей частиц, не изменяет механические свойства системы.
Воснове закона сохранения момента импульса лежит изотропия пространства, т. е. одинаковость свойств пространства по всем направлениям (симметрия по отношению к повороту осей координат). Одинаковость следует понимать в том смысле, что поворот замкнутой системы, как целого, не отражается на её механических свойствах.
Между законами типа основного уравнения динамики и законами сохранения имеется принципиальная разница. Законы динамики дают нам представление о детальном ходе процесса. Так, если задана сила, действующая на материальную точку и начальные условия, то можно найти закон движения, траекторию, величину и направление скорости в любой момент времени и т. п. Законы же сохранения не дают нам прямых указаний на то, как должен идти тот или иной процесс. Они говорят лишь о том, какие процессы запрещены и потому в природе не происходят.
Таким образом, законы сохранения проявляются как принципы запрета: любое явление, при котором не выполняется хотя бы один из законов сохранения, запрещено, и в природе такие явления никогда не наблюдаются. Всякое явление, при котором не нарушается ни один из законов сохранения, в принципе может происходить. Фундаментальность законов сохранения заключается в их универсальности. Они справедливы при изучении любых физических процессов (механических, тепловых, электромагнитных и др.). Они одинаково применимы в релятивистском и нерелятивистском движении, в микромире, где справедливы квантовые представления, и в макромире, с его классическими представлениями.
21.В физике механи ческаяэне ргия описывает сумму потенциальнои и кинетическои энергии, имеющихся в компонентах механической системы. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.
Полная механическая энергия может изменяться в результате следующих причин: внешнего воздействия на систему (толчки, приближение извне магнита, заряженных тел и т.п.); наличия внутренних неконсервативных сил. Например, силы сопротивления вызывают уменьшение механической энергии системы "шар, Земля, воздух, нить".
Зако нсохране нияэне ргии— фундаментальный закон природы, установленный эмпирически и заключающийся в том, что для изолированной физической системы может быть введена скалярная физическая величина, являющаяся функцией параметров системы и называемая энергией, которая сохраняется с течением времени. Поскольку закон сохранения энергии относится не к конкретным величинам и явлениям, а отражает общую, применимую везде и всегда, закономерность, то его можно именовать не законом, а принципом сохранения энергии.
В ньютоновской механике формулируется частный случай закона сохранения энергии — Закон сохранения механической энергии, звучащий следующим образом Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
Проще говоря, при отсутствии диссипативных сил (например, сил трения) механическая энергия не возникает из ничего и не может исчезнуть в никуда.
По энергетическому признаку динамические системы делятся на консервативные и неконсервативные. онсервативные системы характеризуются неизменным во времени запасом энергии. В механике их
называют гамильтоновыми.
Динамические системы с изменяющимся во времени запасом энергии называются неконсервативными. Системы, в которых энергия уменьшается во времени из-за трения или рассеяния, называются диссипативными. В соответствии с этим системы, энергия которых во времени нарастает, называются системами с отрицательным трением или отрицательной диссипацией. Такие системы можно рассматривать как диссипативные при смене направления отсчета времени на противоположное.

22.Незамкнутая система тел — это группа тел, взаимодействующих не только между собой, а и ещё с какими-то телами, «посторонними» для данной группы тел. В таком случае общий импульс системы (группы) тел не будет сохраняться. Он будет изменяться. А изменение импульса системы тел равно импульсу той силы, которая приложена к системе. Например. Стоящего на льду конькобежца может заставить сдвинуться с места (изменить импульс!) толчок его товарища. Но если конькобежец будет тянуть одной своей рукой другую, то это не изменит его импульс.
23.Ньютона законы механики, три закона, лежащие в основе т. н. классической механики. Сформулированы И. Ньютоном (1687). Первый закон: "Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние". Второй закон: "Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует". Третий закон: "Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны".
Н. з. м. появились как результат обобщения многочисленных наблюдений, опытов и теоретических исследований Г. Галилея, Х. Гюйгенса, самого Ньютона и др.
Согласно современным представлениям и терминологии, в первом и втором законах под телом следует понимать материальную точку, а под движением — движение относительно инерциальной системы
отсчёта. Математическое выражение второго закона в классической механике имеет вид:
или mw = F, где m — масса точки, u — её скорость, a w — ускорение, F— действующая сила.
Н. з. м. перестают быть справедливыми для движения объектов очень малых размеров (элементарные частицы) и при движениях со скоростями, близкими к скорости света.
24. Основными законами вращательного движения твердого тела являются:
Уравнение (закон) динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.
или
где: JZ - момент инерции тела относительно оси Z; -угловое ускорение.
Закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.
Общими законами для поступательного и вращательного движения твердого тела служат:
Закон сохранения механической энергии: полная механическая энергия системы тел остается неизменной при любых движениях тел системы.
Общефизический закон сохранения энергии: энергия не может возникнуть из ничего и не может в никуда
исчезнуть, она может только переходить из одной формы в другую.
Если алгебраическая сумма моментов всех пар сил, приложенных к телу, имеющему ось вращения, не равна нулю, то тело приобретает угловое ускорение, числовое значение которого прямо пропорционально вращающему моменту Мвр: Мвр = Jε.
В этом уравнении, выражающем основной закон динамики для вращательного движения тела,
множителем пропорциональности является момент инерции тела. Тело с большим моментом инерции труднее привести во вращение.

25.Плоскопараллельноедвижение (плоское движение) — вид движения абсолютно твёрдого тела, при котором траектории всех точек тела располагаются в плоскостях, параллельных заданной плоскости.
Примером плоскопараллельного движения по отношению к вертикальной плоскости, относительно которой тело движется в параллельном направлении, является качение колеса по горизонтальной дороге. Пример плоскопараллельного движения относительно плоскости чертежа — качение колеса по горизонтальной дороге. Все точки колеса движутся параллельно плоскости рисунка.
Здесь плоскопараллельное движение в каждый момент времени может быть представлено в виде суммы двух движений — полюса C, являющегося не чем иным, как центром вращения колеса в связанной с ним системе координат (в общем случае по любой траектории на плоскости с точки зрения неподвижного наблюдателя) и вращательного движения остальных точек тела вокруг этого центра.
Вращение тела в случае его плоско-параллельного движения не является необходимым признаком последнего.В случае отсутствия проскальзывания трение соприкасающейся с опорой части колеса есть трение покоя, а коэффициент трения покоя, как правило, больше коэффициента трения скольжения. Поэтому не целесообразно доводить торможение до состояния, когда колёса идут "юзом".
Маятник Максвелла представляет собой диск, неподвижно закрепленный на тонком стержне (рис.1). На концах стержня симметрично относительно диска закреплены нити, с помощью которых маятник подвешен к штативу. При вращении маятника нити могут наматываться на стержень или сматываться с него, обеспечивая тем самым перемещение маятника вверх - вниз. Если, намотав нити на ось, поднять маятник на некоторую высоту и
отпустить его, то он начнет опускаться под действием силы тяжести, приобретая одновременно и вращательное движение. В нижней точке, когда маятник опустится на полную длину нитей, поступательное движение вниз прекратится. Нити станут наматываться на вращающийся по инерции стержень, а маятник начнет подниматься вверх, постепенно замедляя свое вращение. После достижения наивысшей точки цикл колебательного движения возобновится.
Если mg — сила тяготения; T — сила натяжения одной нити; R — радиус стержня; J — момент инерции маятника; тогда уравнение для поступательного движения можно записать так:
mg − 2T = ma,
где a — ускорение центра масс. Уравнение для вращательного движения при этом будет иметь вид:
M = mR(g − a) = 2TR=J ε,
где ε – угловое ускорение.
Маятник движется с постоянным ускорением. Если h – расстояние, пройденное за время t, при равноускоренном движении с нулевой начальной скоростью, то момент инерции можно найти по формуле:
J=mR2((gt2)/(2h)-1).
26. Группу тел, взаимодействующих не только между собой, но и с телами, не входящими в состав этой группы, называют незамкнутой системой. Силы, с которыми на тела данной системы действуют тела, не входящие в эту систему, называют внешними (обычно внешние силы обозначают буквой F). Рассмотрим взаимодействие двух тел в незамкнутой системе. Изменение импульсов данных тел происходит как под действием внутренних сил, так и под действием внешних сил.
Согласно второму закону Ньютона, изменения импульсов рассматриваемых тел у первого и второго тел составляют
Dр1=f1t+F1t (3.5)Dр2=f2t+F2t (3.6)где t - время действия внешних и внутренних сил.
Почленно сложив выражения (3.5) и (3.6), найдем, что D(p1+p2)=(f1+f2)t +(F1+F2)t (3.7)
В этой формуле р=р1+р2 - полный импульс системы, f1+f2=0 (так как по третьему закону Ньютона (f1=- f2), F1+F2=F - равнодействующая всех внешних сил, действующих на тела данной системы. С учетом сказанного формула (3.7) принимает вид Dр=Ft. (3.8)
Из (3.8) видно, что полный импульс системы изменяется только под действием внешних сил. Если же система замкнутая, т. е. F=0, то Dр=0 и, следовательно, р=const. Таким образом, формула (3.4) является частным случаем формулы (3.8), которая показывает, при каких условиях полный импульс системы сохраняется, а при каких - изменяется..
Если сист. незамкнута, но действующие на неё силы таковы, что их главный вектор тождественно
какую-либо неподвижную ось тождественно равна нулю, то проекция на ту же ось вектора импульса
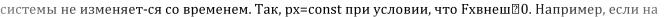
систему действуют внешние силы, которые направлены только вертикально, то горизонтальная составляющая импульса системы не изменяется (пример: маятник на тележке на рельсах).
1. лектромагнитное поле, особая форма материи, посредством которой осуществляется взаимодействие между электрически заряженными частицами . п. в вакууме характеризуется вектором напряжённости электрического поля Е и магнитной индукцией В, которые определяют силы, действующие со стороны поля на неподвижные и движущиеся заряженные частицы. Наряду с векторами Е и В, измеряемыми непосредственно, . п. может характеризоваться скалярным j и векторным А потенциалами, которые определяются неоднозначно, с точностью до градиентного преобразования В среде . п. характеризуется дополнительно двумя вспомогательными величинами: напряжённостью магнитного поля Н и электрической индукцией D . Поведение . п. изучает классическая электродинамика, в произвольной среде оно описывается Максвелла уравнениями, позволяющими определить поля в зависимости от распределения зарядов и токов.
лектри ческии заря—дэто связанное с телом свойство, позволяющее ему быть источником электрического поля и участвовать в электромагнитных взаимодействиях. Заряд является количественной характеристикой. Единица измерения заряда в СИ — кулон — электрический заряд, проходящий через поперечное сечение проводника при силе тока 1А за время 1с. Впервые электрический заряд был введён в законе улона в 1785 году. Заряд в один кулон очень велик. Если бы два носителя заряда (q1 = q2 = 1 л) расположили в вакууме на расстоянии 1 м, то они взаимодействовали бы с силой 9×109 H.
Свойства электрического заряда :
-Заряд бывает двух видов, называемых положительным и отрицательным:
-заряды одного вида отталкиваются друг от друга, заряды разных видов - притягиваются, причем сила отталкивания равна по модулю силе притягивания; -число положительных и отрицательных зарядов во Вселенной одинаковое.
-Полный электрический заряд изолированной системы сохраняется. лектрический заряд - релятивистски инвариантен, т. е. его величина не зависит от скорости системы отсчета, как бы велика она ни была.
-Величина заряда может принимать только дискретные значения: -минимальный заряд частицы e = 1.60·1019 л;
-любой заряд q кратен минимальному, т.е. q=Ne, где N - целое число;
-минимальные положительный и отрицательный заряды равны по абсолютной величине.
2. НАПРЯЖЕННОСТЬ ПОЛЯ — векторная величина, характеризующая электрическое или магнитное поле.
Напряженность электрического поля — векторная величина Е, равная отношению силы dF, действующей на положительный заряд dQ, помещенный в некоторую точку электрического поля, к величине этого заряда: Е = dF / dQ; dimE = LMT−3I−1, единица — вольт на метр (В/м).
Вольт на метр равен напряженности однородного электрического поля, создаваемой разностью потенциалов 1 В между точками, находящимися на расстоянии 1 м на линии напряженности поля. Напряженность магнитного поля — векторная величина Н, характеризующая магнитное поле. Размерность и единица ее могут быть определены по формуле напряженности поля в центре длинного соленоида:Н = nI;dimH = L−1I,единица — ампер на метр (А/м).
Ампер на метр равен напряженности магнитного поля в центре длинного соленоида с равномерно распределенной обмоткой, по которой проходит ток силой I/n А, где n — число витков на участке соленоида длиной 1 м.

3. сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу.Сила, действующая на электрический заряд 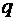 , движущийся со скоростью
, движущийся со скоростью 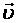 в
в
магнитном поле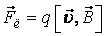 , (18)где
, (18)где 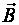 – вектор магнитной индукции поля.
– вектор магнитной индукции поля.
· Модуль силы, действующей на заряженную частицу, движущуюся в магнитном поле
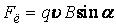 , (19)где
, (19)где 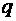 – модуль заряда частицы;
– модуль заряда частицы; 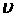 – модуль вектора скорости;
– модуль вектора скорости; 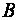 – модуль вектора индукции магнитного поля,
– модуль вектора индукции магнитного поля, 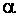 – угол между векторами
– угол между векторами 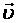 и
и 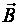 .
.
· Направление силы 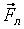 определяется по правилу левой руки:
определяется по правилу левой руки:
если ладонь левой руки расположить так, чтобы в нее входил вектор магнитной индукции 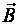 , а четыре вытянутых пальца направить вдоль скорости движения положительного заряда (против направления движения отрицательного заряда), то отогнутый на 90° большой палец покажет направление силы, действующей на заряд.
, а четыре вытянутых пальца направить вдоль скорости движения положительного заряда (против направления движения отрицательного заряда), то отогнутый на 90° большой палец покажет направление силы, действующей на заряд.
· Если заряд движется в области, где существуют одновременно электрическое и магнитное поля,
то на него действует полная сила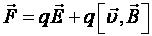 , формула называется формулой Лоренца. При движении заряженной частицы в области пространства, занятой одновременно и
, формула называется формулой Лоренца. При движении заряженной частицы в области пространства, занятой одновременно и
электрическим и магнитным полями характер ее движения зависит от направления этих полей и величины сил, действующих с их стороны, а также от скорости частицы.
► Векторы 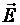 и
и 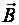 взаимно-перпендикулярны и скорость
взаимно-перпендикулярны и скорость 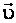 положительно заряженной частицы перпендикулярна силовым линиям этих полей. В этом случае на частицу действуют две силы:
положительно заряженной частицы перпендикулярна силовым линиям этих полей. В этом случае на частицу действуют две силы:
электрическая 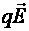 и магнитная
и магнитная 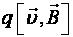 , которые могут быть как сонаправлены, так и противоположно направлены. Если силы противоположно направлены и равны по модулю (
, которые могут быть как сонаправлены, так и противоположно направлены. Если силы противоположно направлены и равны по модулю (
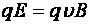 ), то частица будет двигаться равномерно и прямолинейно, согласно первому закону Ньютона.
), то частица будет двигаться равномерно и прямолинейно, согласно первому закону Ньютона.
В случае если силы не уравновешивают друг друга, то движение частицы будет сложным: она будет двигаться с ускорением вдоль линии напряженности электрического поля и совершать вращательное движение вокруг линии индукции магнитного поля.
Если силы, действующие на движущуюся заряженную частицу сонаправлены, то движение частицы также будет представлять суперпозицию двух движений: прямолинейного с ускорением вдоль
линий вектора  и вращательного вокруг линий вектора
и вращательного вокруг линий вектора 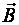 .
.
►Частицавлетаетвобластьпространствапараллельновекторам 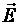 и
и 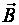 . В этом случае на нее действует только электрическая сила
. В этом случае на нее действует только электрическая сила 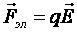 (сила Лоренца
(сила Лоренца 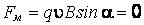 , так как
, так как 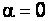
и |
). Под действием этой силы |
частица движется прямолинейно с ускорением |
. |
4.Электрическое поле — пространство, обладающее свойством действовать с силой на электрический заряд, помещённый в это поле.Как показывает опыт, эта электрическая сила F пропорциональна величине пробного заряда q, находящегося в исследуемой точке
поля.Поэтому отношение — уже не будет зависеть от величины пробного заряда. Оно определяется только свойством поля в данной точке. Это отношение принято в качестве силовой характеристики электрического поля и получило названиенапряженность.
(1.2)
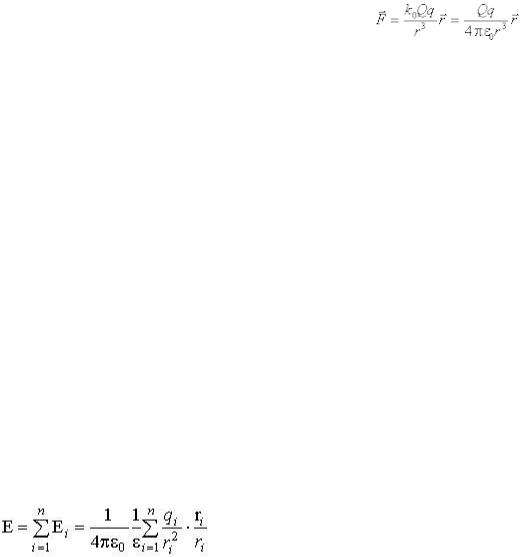
Пусть поле создаётся точечным зарядом Q. Внесём в точку А этого поля пробный точечный заряд q (рис. 1.3.) На него в поле будет действовать сила, равная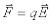 .
.
Но эту же силу можно записать, воспользовавшись законом Кулона (1.1)
Сопоставив эти два уравнения, легко получить выражение для напряжённости электрического поля, созданного точечным зарядом Q:
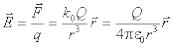 (1.3)Напряжённость поля точечного заряда прямо пропорциональна величине заряда Q, создающего поле, и обратно пропорциональна квадрату расстояния от заряда, до той точки поля, в которой измеряется напряжённость.
(1.3)Напряжённость поля точечного заряда прямо пропорциональна величине заряда Q, создающего поле, и обратно пропорциональна квадрату расстояния от заряда, до той точки поля, в которой измеряется напряжённость.
Обозначим: q - заряд, создающий поле,
q0 - заряд, помещенный в поле (внешний заряд).
Закон Кулона: 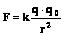 . Напряженность поля:
. Напряженность поля: 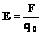 .
.
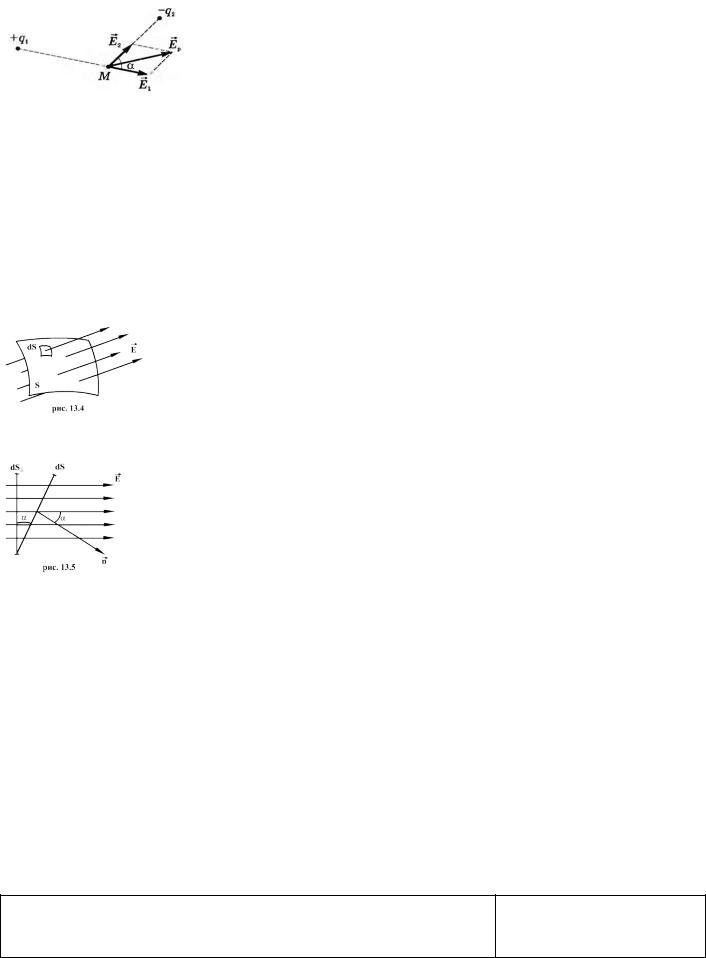
Тогда напряженность поля точечного заряда: 
лектрическое поле создается как неподвижными, так и движущимися зарядами. О наличии электрического поля можно судить, прежде всего, по его способности оказывать силовое действие на электрические заряды, движущиеся и неподвижные, а также по способности индуцировать электрические заряды на поверхности проводящих нейтральных тел.
Поле, создаваемое неподвижными электрическими зарядами, называют стационарным электрическим, или электростатическим полем. Оно представляет собой частный случай электромагнитного поля, посредством которого осуществляются силовые взаимодействия между электрически заряженными телами, движущимся в общем случае произвольным образом относительно системы отсчета.
Принцип суперпозиции. Напряжённость поля, создаваемого системой неподвижных точечных
зарядов q1, q2, q3, , qn, равна векторной сумме напряжённостей электрических полей, создаваемых каждым из этих зарядов в отдельности:
где ri – расстояние между зарядом qi и рассматриваемой точкой поля.
5.Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга. Если в пространстве имеется система заряженных тел, то в каждой точке этого пространства существует силовое электрическое поле. Оно определяется через силу, действующую на пробный заряд, помещённый в это поле. Пробный заряд должен быть малым, чтобы не повлиять на характеристику электростатического поля.
лектростатическое поле характеризуется напряженностью электрического Е, которая является его силовой характеристикой: Напряженность электростатического поля показывает, с какой силой электростатическое поле действует на единичный положительный электрический,помещенный в данную точку поля. Направление вектора напряженности совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующий на отрицательный заряд.
лектростатическое поле является стационарным (постоянным), если его напряженность не изменяется с течением времени. Стационарные электростатические поля создаются неподвижными электрическими зарядами.
При нципсуперпози ции— один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что
напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть сумма напряженностей полей отдельных зарядов.
Ди оль (от ди... и греч. pólos — полюс) электрический, совокупность двух равных по абсолютной величине разноимённых точечных зарядов, находящихся на некотором расстоянии друг от друга. Основной характеристикой электрического Д. является его дипольный момент — вектор, направленный от отрицательного заряда к положительному и численно равный произведению заряда е на расстояние l между зарядами:р = el. Дипольный момент определяет электрическое поле Д. на большом расстоянии R от Д. (R"l), а также воздействие на Д. внешнего электрического поля.
Вдали от Д. его электрическое поле Е убывает с расстоянием как 1/R3, т. е. быстрее, чем поле точечного заряда (~ 1/R2).
6.Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности NE.
Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4).
Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).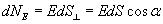 где
где 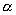 - угол между силовой линией и нормалью
- угол между силовой линией и нормалью 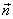 к площадке dS;
к площадке dS; 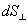 - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда
- проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда
поток напряженности поля через всю поверхность площадки S будет равен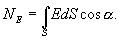
Так как 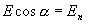 , то
, то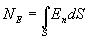
7. Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью. Применяется отдельно для вычисления электростатических полей.
Потоком вектора напряженности наз. величина Ф, равная произведению модуля вектора напряженности на площадь контура S, ограничивающую некоторую площадь, и на косинус угла между вектором напряженности и нормалью (перпендикуляром) к площадке.

Если считать, что напряженность пропорциональна числу силовых линий, приходящихся на единицу площади поверхности (т.е. густоте), то поток напряженности пропорционален полному числу силовых линий, пересекающих данный контур.
Поток линий напряженности электростатического поля через произвольную замкнутую поверхность прямо пропорционален величине заряда, находящегося в области пространства, ограниченного данной поверхностью.
8.Рассмотрим поле, создаваемое бесконечной прямолинейной нитью с линейной плотностью заряда, равной 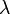 . Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии
. Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии 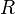 от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом
от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом 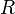 и высотой
и высотой 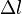 . Тогда поток напряжённости через эту поверхность по теореме Гаусса таков (в единицах СИ):
. Тогда поток напряжённости через эту поверхность по теореме Гаусса таков (в единицах СИ):
Всилу симметрии
1.вектор напряженности поля направлен перпендикулярно нити, прямо от нее (или прямо к ней).
2.модуль этого вектора в любой точке поверхности цилиндра одинаков.
Тогда поток напряжённости через эту поверхность можно рассчитать следующим образом:
Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю (вследствие направления E по касательной к ним). Приравнивая два полученных выражения для 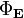 , имеем:
, имеем:
9.Рассмотрим поле, создаваемое бесконечной однородно заряженной плоскостью с везде одинаковой поверхностной плотностью заряда 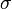 . Представим себе мысленно цилиндр с образующими, перпендикулярными к заряженной плоскости, и основаниями (площадью
. Представим себе мысленно цилиндр с образующими, перпендикулярными к заряженной плоскости, и основаниями (площадью 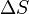 каждое), расположенными относительно плоскости симметрично (см. рисунок).
каждое), расположенными относительно плоскости симметрично (см. рисунок).
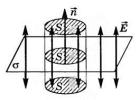 В силу симметрии:
В силу симметрии:
1. |
Все векторы напряжённости поля (в том числе |
и |
) — перпендикулярны заряженной плоскости. |
2. |
. |
|
|
Поток вектора напряжённости равен (в силу (1)) потоку только через основания цилиндра, а он, в силу того,
что |
и |
перпендикулярны этим основаниям и в силу (2), равен просто |
. |
|
Применив теорему Гаусса, и учитывая |
, получим (в системе СИ): |
|
||
из чего

10.Сфера радиусом R. Пусть заряд +q равномерно распределён по сферической поверхности радиуса R. Распределение заряда по поверхности характеризуется поверхностной плотностью заряда.Поверхностной плотностью заряда называют отношение заряда к площади поверхности, по которой он распределён.
-Сферически симметричный заряд с концентрической сферической пустотой (или незаряженной областью) в середине, не создает внутри этой пустоты поля (напряженность поля там равна нулю).
-Вообще поле на расстоянии r от центра создается только теми зарядами, которые находятся глубже к центру. то поле можно рассчитать по закону улона: , только под Q здесь следует понимать суммарный заряд шаровой области радиусом r (а это означает, что зависимость от r в итоге отличается от кулоновской, поскольку с ростом r растет Q, по крайней мере пока r не больше радиуса всей заряженной области — если только она в свою очередь конечна).
-При r, больших радиуса заряженной области (если он конечен), выполняется самый обычный закон улона (как для точечного заряда). то объясняет, например, почему обычный закон улона работает
для равномерно заряженных шаров, сфер, планет со структурой близкой к сферически симметричной даже вблизи их поверхности (например, почему вблизи поверхности Земли гравитационное поле достаточно близко к полю точечной массы, сосредоточенной в центре Земли).
-В интересном частном случае равномерно заряженного шара, его электрическое (или гравитационное) поле оказывается внутри шара пропорциональным расстоянию до центра.
11. онденса тор (от латcondensare. — «уплотнять», «сгущать») — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля.
онденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.
лектроемкость плоского конденсатора C=qU, где U = E d, d — расстояние между пластин. Следовательно, Поле плоского конденсатора можно рассматривать как совокупность полей двух бесконечных разноименно заряженных плоскостей. Напряженность поля можно найти по принципу суперпозиции E=2E1=σε0ε
— напряженность поля конденсатора, где σ — поверхностная плотность заряда на обкладках конденсатора. Рассчитаем емкость плоского конденсатора.
Обозначим площадь одной обкладки S, расстояние между ними d. Так как , q = σS , U = Ed, то C=σSEd, где E=σε0ε.
Конденсаторы находят широкое применение во многих областях радио- и электротехники.
При быстром разряде конденсатора можно получить импульс большой мощности, например, в фотовспышках, электромагнитных ускорителях, импульсных лазерах и т. п.
Так как конденсатор способен длительное время сохранять заряд, то его можно использовать в качестве элемента памяти или устройства хранения электрической энергии.
Емкость конденсатора заметно изменяется при малейших изменениях параметра конденсатора. Так малое изменение расстояния между обкладками учитывается в измерителях малых перемещений, изменение состава диэлектрика при изменении влажности фиксируется в измерителях влажности, учет изменения высоты диэлектрика между обкладками конденсатора позволяет измерять уровень жидкости и т.п.
Конденсаторы (совместно с катушками индуктивности и/или резисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепей обратной связи, колебательных контуров и т. п.
12.Закон Био—Савара—Лапла са— физический закон для определения модуля вектора магнитной индукции в любой точке магнитного поля, порождаемого постоянным электрическим током на некотором рассматриваемом участке. Был установлен экспериментально в 1820 году Био и Саваром.

Лаплас проанализировал данное выражение и показал, что с его помощью путём интегрирования, в частности, можно вычислить магнитное поле движущегося точечного заряда, если считать движение одной заряженной частицы током.
Пусть постоянныйтечётток по контуру, находящемуся в вакууме,— точка, в которой ищется пол тогдаиндукциямагнитного поля в этой точке выражается интеграломСИ) (в системе
Направление перпендикулярно , то есть перпендикулярно плоскости,лежат,в которойи о совпадает с касательноймагнитнойк линиииндукции.Это направление может быть найдено по п нахождения линий магнитнойправилуиндукцииправого(винта): направление вращения головки вин направление , если поступательное движение буравчика соответствует направлен Модуль вектораопределяетсвыражением (в системеСИ)
Закон Био—Савара—Лапласа играет в магнитостатике ту же роль, что и закон улона в электростатике. Закон Био—Савара—Лапласа можно считать главным законом магнитостатики, получая из него остальные ее результаты.
13.Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется ринци у су ер озиции: Если магнитное оле создается
несколькими роводниками с током, то индукция результирующего оля есть векторная сумма индукций олей, создаваемых каждым роводником в отдельности. ндукцию проводника с током можно представить как векторную сумму элементарных индукций создаваемых отдельными участками проводника. На опыте невозможно осуществить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад в магнитную
индукцию результирующего магнитного поля, создаваемый малым участком Δl проводника с током I.
Здесь r – расстояние от данного участка Δl до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ0 – магнитная постоянная. Направление
вектора 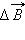 определяется правилом буравчика.
определяется правилом буравчика.
14. Расчеты магнитного поля токов часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае расчеты можно выполнять с помощью теоремы о циркуляции вектора магнитной индукции, которая в теории магнитного поля токов играет ту же роль, что и теорема
Гаусса в электростатике. Поясним понятие циркуляции вектора 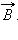 Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление обхода контура. На каждом отдельном малом участке Δl этого контура
Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление обхода контура. На каждом отдельном малом участке Δl этого контура
можно определить касательную составляющую 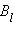 вектора
вектора 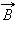 в данном месте, то есть определить проекцию вектора
в данном месте, то есть определить проекцию вектора 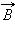 на направление касательной к данному участку контура (рис. 4.17.2).
на направление касательной к данному участку контура (рис. 4.17.2).
