Жорданова нормальная форма линейного оператора и матрицы

Определение.Жордановой клеткойпорядканазывается матрица порядкавида

Жордановой матрицейназывается матрица, состоящая из жордановых клеток.

Лемма.Для нильпотентного операторана-мерном векторном пространствесуществует базис, в котором матрица оператора жорданова (с нулями на главной диагонали).

Теорема.Если характеристический многочленлинейного оператораразлагается на линейные множители, то существует базиспространства, в котором матрица оператора жорданова (на диагонали стоят собственные значения оператора).

Следствие.Для каждого комплексного оператора существует жорданов базис.

Обозначим через количество жордановых клеток порядкасна диагонали. Через, гдематрицы, будем обозначать матрицу, вдоль диагонали которой идут матрицы, а остальные нули.

Теорема.Еслии-- жордановы матрицы операторав разных базисах, то для всякогои всякогоимеет место равенство, т.е. матрицыиотличаются только порядком расположения жордановых клеток ``вдоль'' диагонали.

Следствие.Жорданова клетка не диагонализируема (иначе получили бы две разные жордановы формы).

Определение.Матрицаподобнаматрице, пишут, если существует такая невырожденная матрица, что.

Замечание.Отношение подобияявляется отношением эквивалентности:

рефлексивность:,

симметричность: если, то,

транзитивность: еслии, то.

Определение.Жордановой формойквадратной матрицыназывается жорданова матрица, которая подобна.

Теорема.Каждаяматрица над полем комплексных чиселобладает жордановой формой, причем единственной (с точностью до порядка жордановых клеток).

Двематрицы надподобны тогда и только тогда, когда их жордановы формы совпадают (с точностью до порядка жордановых клеток).

Теорема.Линейный операторв комплексном-мерном пространстведиагонализируем тогда и только тогда, когда его минимальный многочлен не имеет кратных корней.

Билет 9

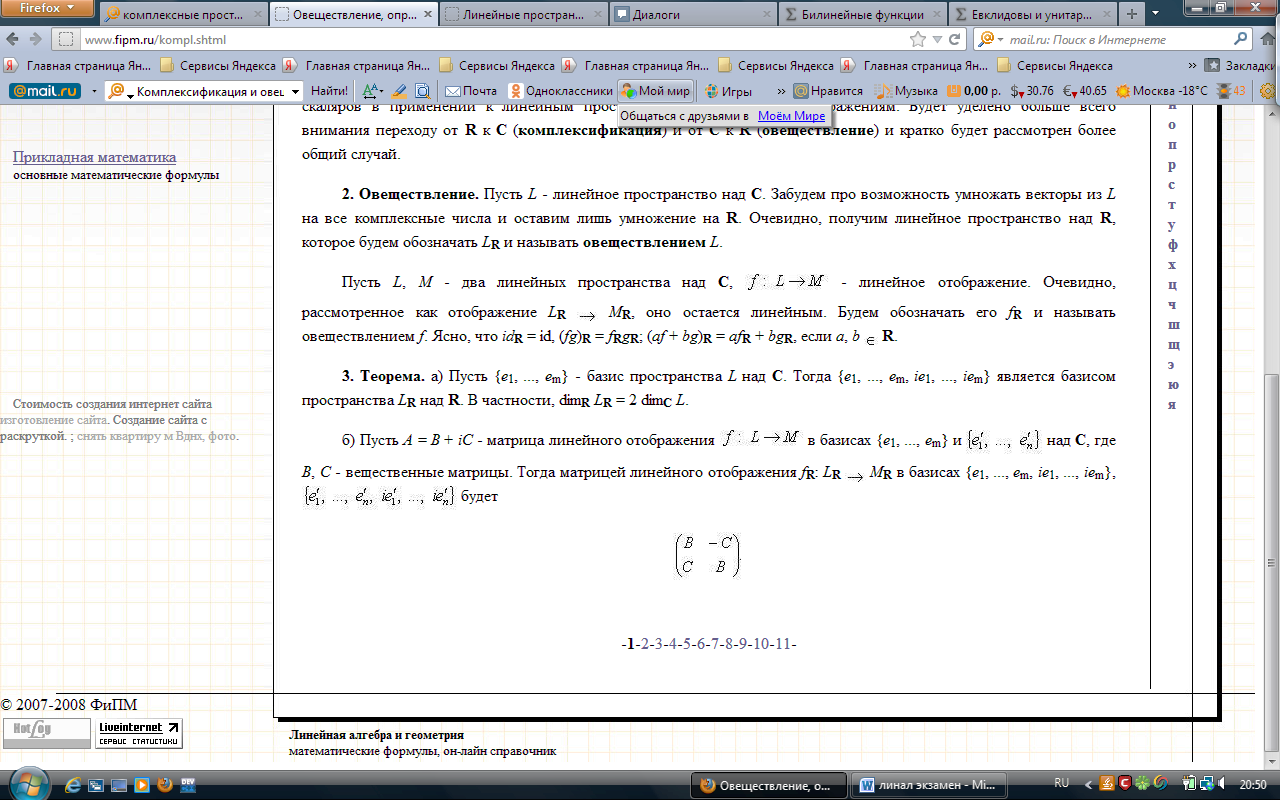
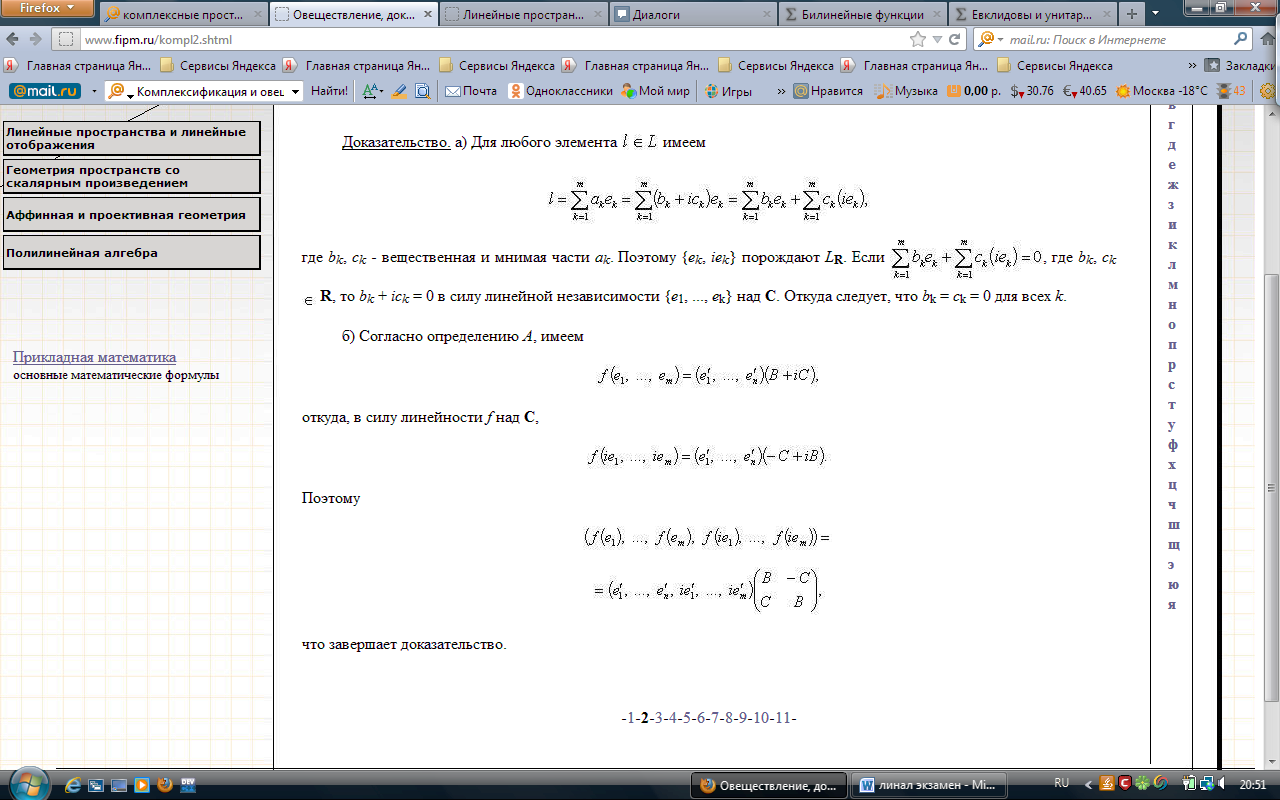
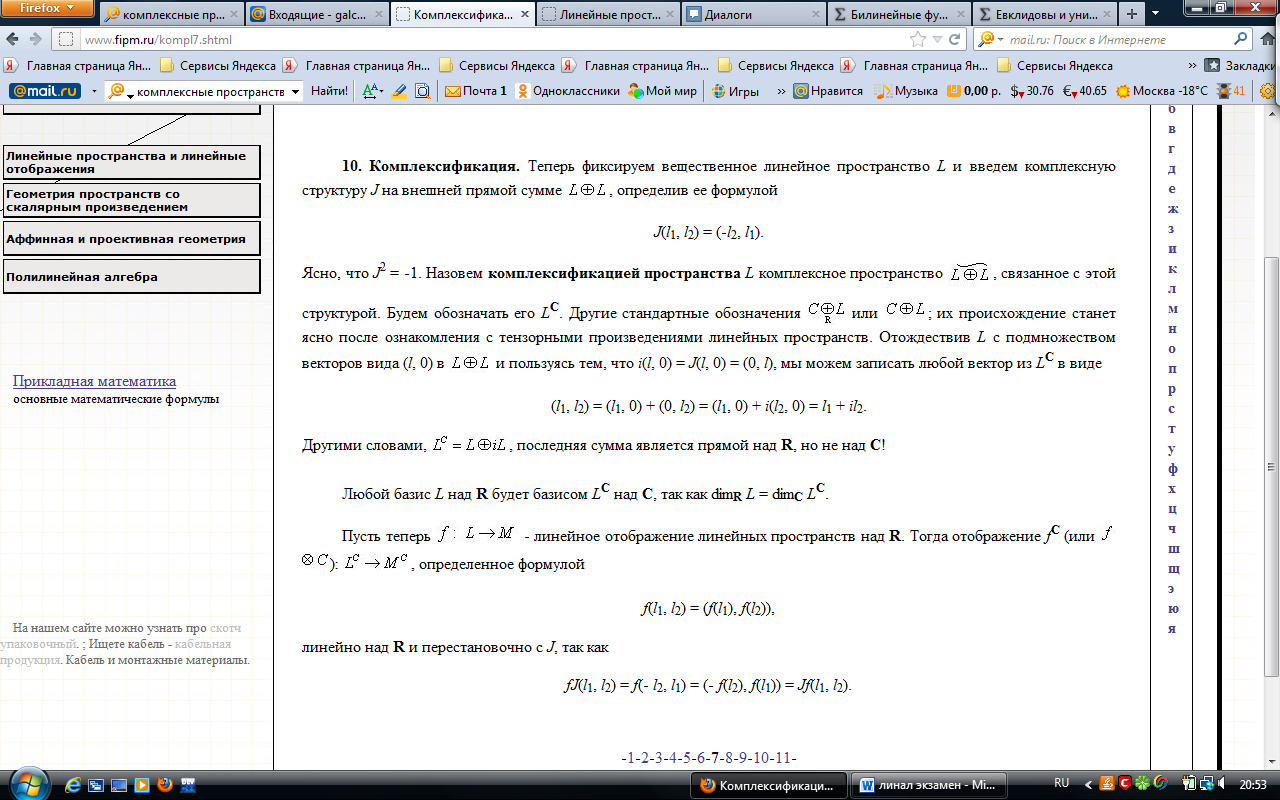
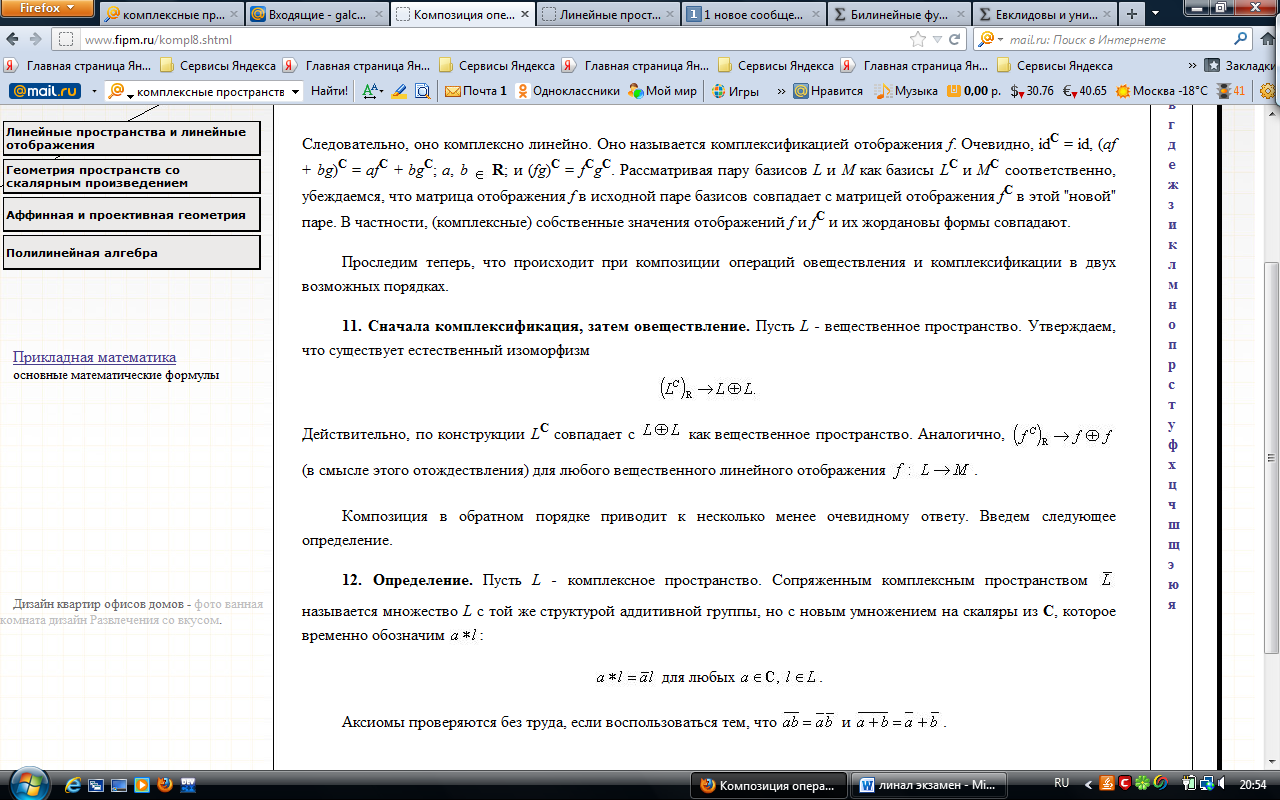
Комплексные линейные пространства

См билет 8 –про структуры

Билет 10+билет 11

Евклидовы и унитарные пространства

Определение.Евклидовым пространствомназывается вещественное линейное пространствос заданной наположительно определенной симметрической билинейной функцией, которая называется скалярным произведением и обозначается.

Пример.Рассмотрим примеры евклидовых пространств.

Арифметическое пространство. Еслии-- столбцы координат векторовисоответственно в стандартном базисе, то.

Пространствонепрерывных функций на. Для любых двух функцийполагаем.

Пространство многочленов степени не больше. Для любых двух многочленовполагаем.

Определение.Пусть---мерное евклидово пространство с базисом.Матрица Граммабазиса-- это матрица

Определитель матрицы Грамманазываетсяопределителем Грамма.

Определение.Вектораназываютсяортогональными, если.Длинавектора-- это неотрицательное число. Если, тоуголмеждуиопределяется по формуле.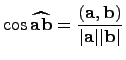

Теорема.Если векторыортогональны, то.

Теорема.Если-- ортогональная система ненулевых векторов, то она линейно независима.

Теорема.[Неравенство Коши-Буняковского] Для любых векторовевклидова пространствасправедливо неравенство. Причем равенство имеет место тогда и только тогда, когда векторыилинейно зависимы.

Следствие.[Неравенство Коши] Для всяких векторов чиселисправедливо неравенство.

Следствие.[Неравенство Буняковского] Для любых чисели любых непрерывных функцийсправедливо неравенство.

Следствие.[Неравенство треугольника] Для всяких векторовевклидова пространствасправедливо неравенство.

Определение.Унитарнымпространством называется линейное пространство над полем комплексных чисел, на котором определена эрмитова положительно определенная функция. Она обозначается также.

Теорема.Для любых векторовунитарного пространствасправедливо неравенство.

Определение.Базисв евклидовом (унитарном) пространственазываетсяортогональным нормированным(ортонормальным), если для любых базисных векторов справедливо равенство.

Замечание.Из следствия следует, существования такого базиса. Заметим, что матрица Грамма в этом базисе единична.

Определение.Пусть-- произвольная квадратная матрица над. Система столбцов вназываетсяортонормальнойсистемой, если. Матрицаназываетсяортогональной, если система ее столбцов ортонормальна.

Теорема.Для всякой квадратной вещественной матрицыпорядкаследующие условия равносильны:

система строк матрицыортонормальна;

система столбцов матрицыортонормальна;

.

Следствие.Если-- ортогональна, то.

Если-- ортогональна, то-- ортогональна.

Еслии-- ортогональные матрицы, то матрицатоже ортогональна.

Замечание.Ортогональные матрицы образуют группу.

Определение.Комплексная матрицаназываетсяунитарной, если.

Теорема.Если-- унитарная матрица, то.

Если-- унитарная матрица, то-- унитарная матрица.

Еслии-- унитарные матрицы, то матрицатоже унитарная.

Замечание.Унитарные матрицы образуют группу.

Теорема.Пусть-- ортонормальный базис евклидова (унитарного) пространства. Базисявляется ортонормальным тогда и только тогда, когда матрица перехода от базисакявляется ортогональной (унитарной).

Определение.Изоморфизмомевклидовых (унитарных) пространствиназывается такой изоморфизм линейных пространств, для которогодля любых векторов.

Теорема.Два конечномерных евклидовых (унитарных) пространстваиизоморфны тогда и только тогда, когда.

Пусть ---мерное евклидово пространство, и-- его сопряженное. Положим для любого векторапо определению, где.

Теорема.является линейной функцией на, т.е..

Имеется естественный изоморфизммежду-мерными евклидовым пространствоми.

Процесс ортогонализации.Пусть даны линейно независимые векторы. Требуется найти такие векторы, чтоприи. Тогдаи.

Берем . Хотими, тогда().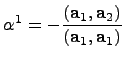

На -ом шаге получаем,и.

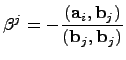Определение.Определитель матрицы Грамма векторовназываетсяквадратом -мерного объема параллелепипеда, натянутого на.

Теорема.Определитель Грамма не меняется при процессе ортогонализации.