11.3. Расчет деформаций естественных оснований

одени нормативными документами не требуется. Однако в ряде случаев, например при совместном расчете системы основание^» сооружение, такой расчет необходим.

Расчет осадок уплотнения ведется в предположении, что грунт подчиняется законам линейно-деформируемой среды, когда дефор­мации линейно зависят от давлений (первая фаза работы грунта, см. рис. II. 5, с). Теоретически максимальное давление на грунт, при котором существует линейная зависимость, определяется отсут­ствием под подошвой фундамента пластических зон (зон с нару­шенным равновесием). Однако наблюдения за сооружениями пока­зывают, что небольшое развитие зон пластических деформаций под гранями фундамента может быть допущено при прогнозирова­нии осадок. Среднее давление на основание Я (в тс/м²), при кото­ром еще возможно рассматривать грунт как линейно-деформируе­мую среду, определяется по СИиП И-15-74 формулой

Я-

"^т2 (0,256уц + Ау'ц + с_и с1е_Т11) =

^с1Е?п +ЧРп — 0,5п

(11.14)

(АЬ\_и + Вку'_п + Ос_и)

где /яь т₂ — коэффициенты условий работы основания, приведенные в табл. 11.14; к_в — коэффициент надежности;

Фи — расчетный угол внутреннего трения грунта, залегающего под подошвой фундамента; Ь — ширина подошвы фундамента, м;

Таблица 11.14

Коэффициент т, для соору­жения с жесткой схемой при отношении длины к высоте

Деформации грунтов при их сжатии делятся на деформации уплот­нения и деформации ползучести.

Уплотнение происходит в результате уменьшения пор между частицами грунта (первичная консолидация), что во влажных и во-донасыщенных грунтах связано с вытеснением из пор свободной воды. Вода вытесняется не мгновенно, а в течение некоторого от­резка времени, причем чем меньше размеры пор, тем длительнее нарастание деформации. Так, для полного уплотнения глинистых грунтов иногда требуются десятки лет.

В глинистых грунтах, кроме уплотнения, при некоторых вели­чинах внешнего давления развиваются деформации ползучести (вторичная консолидация). Ползучесть — деформация при постоян­ном давлении — протекает в основном вследствие структурных из­менений в строении глинистых частиц и водно-коллоидных пленок •связной воды. Деформации ползучести протекают весьма медленно и в зависимости от величины внешнего давления и других причин могут быть затухающими и незатухающими. Окончательные дефор­мации сжатия грунтов носят названия конечных (стабилизирован­ных) осадок. Для ответственных сооружений конечные осадки должны быть рассчитаны и сопоставлены с предельно допустимыми деформациями оснований. Расчет протекания деформаций во вре-

42

Крупноблочные с песчаным заполнени­ем и песчаные, кроме мелких и пылева-тых

1,0

1,1 1.1

1,0 1,0 1.0

1,3

1,2

1,2 1,1 1,2

1,3 1,3

1,2 1,2 1.1

1,0

Пески мелкие: сухие и маловлажные насыщенные водой Пески пылеватые: сухие и маловлажные насыщенные водой Крупнообломочные с глинистым за­полнением и глинистые с консистенцией /г<0,5 То же, с консистенцией /1,>0,5

1,1

Прииечании. 1. К жестким относятся конструкции, приспособленные к восприя» тгию дополнительных усилий от деформации основания.

2. Для гибких конструкций т₂=1.

3. При промежуточных значениях / ^ коэффициент Шг определяется по интерполяции.

43

Таблица 11.15

Расчетный угол внутреннего трения у град	А	в	и	Расчетный угол внутреннего трення ю, град	А	в	и
10 12 14 16 18 20 22 24 26 28	0,18 0,23 0,29 0,36 0,43 0,51 0,61 0,72 0,84 0,98	1,73 1,94 2,17 2,43 2,72 3,06 3,44 3,87 4,37 4,93	4,17 4,42 4,69 5,00 5,31 5,66 6,04 6,45 6,90 7,40	30 32 34 36 38 40 42 44 45	1,15 1,34 1,55 1,81 2,11 2,46 2,87 3,37 3,66	5,59 6,35 7,21 8,25 9,44 10,84 12,50 14,48 15,64	7,95 8,55 9,21 9,98 10,80 11,73 12,77 13,96 14,64

■уи — расчетный объемный вес грунта, залегающего под подошвой фун­дамента, тс/м³; к — глубина заложения фундамента, м; ■у'н — расчетный объемный вес грунта, расположенного выше подошвы

фундамента, тс/м³; сц — расчетное значение удельных сил сцепления грунта, расположен­ного под подошной фундамента, тс/м²; А, В, Б — безразмерные коэффициенты, зависящие от угла внутреннего тре­ния, приведенные в табл. 11.15.

Коэффициент т.2 учитывают при жесткой конструкции надфун-даментной части сооружения, если в ней предусмотрены меры для восприятия дополнительных усилий, возникающих при осадках ос­нований. В остальных случаях, в частности в мостах, если пролет­ные строения не рассчитывают на деформации грунтов, коэффици­ент т₂ принимают равным единице.

Коэффициент надежности /с_н зависит от метода определения расчетных характеристик (уц. с_п, у_}, у_п) грунтов; при определении

путем испытания образцов грунтов к_н=1, при определении по таб* лицам без испытания образцов /с_н=1,1.

Для расчета осадок в линейной фазе деформации грунтов необ­ходимо соблюдение условия

Р<Я, (11.15)

где р — среднее давление по подошве фундамента от нормативных нагрузок.

В проектировании сооружений наибольшее применение получи* ли два метода расчета конечных осадок: метод послойного сумми- . рования и метод эквивалентного слоя.

Расчет осадок методом послойного суммирования. Этот метод применяют при сжимаемых грунтах, залегающих на достаточно большую глубину. Основание рассматривают как линейно дефор­мируемое полупространство, загруженное нагрузкой р, равномерно

44

Таблица 11.16

2г			Коэффициент		а для фуида	мента
Ь		прямоугольного		с соотношением сторс		н п=1/Ь, равным
нли								ленточного
г	круглого							при п>10
т=' г		1	1,4	1,8	2,4	3,2	5
0	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000
0,4	0,949	0,960	0,972	0,975	0,976	0,977	0,977	0,977
0,8	0,756	0,800	0,848	0,866	0,875	0,879	0,881	0,881
1,2	0,547	0,606	0,682	0,717	0,740	0,749	0,754	0,755
1,6	0.390	0,449	0,532	0,578	0,612	0,630	0,639	0,642
2	0,285	0,336	0,414	0,463	0,505	0,529	0,545	0,550
2,4	0,214	0,257	0,325	0,374	0,419	0,449	0,470	0,477
2,8	0,165	0,201	0,260	0,304	0,350	0,383	0,410	0,420
3,2	0,130	0,160	0,210	0,251	0,294	0,329	0,360	0,374
3,6	0,106	0,130	0,173	0,209	0,250	0,285	0,320	0,337
4	0,087	0,108	0,145	0,176	0,214	0,248	0,285	0,306
4,4	0,073'	0,091	0,122	0,150	0,185	0,218	0,256	0,280
4,8	0,067	0,077	0,105	0 130	0,161	0,192	0,230	0,258
5,2	0,053	0,066	0,091	0,112	0,141	0,170	0,208	0,239
5,6	0,046	0,058	0,079	0,099	0,124	0,152	0,189	0,223
6	0,040	0,051	0,070	0,087	0,110	0,136	0,172	0,208
6,4	0,036	0,045	0,062	0,077	0,098	0,122	0,158	0,196
6,8	0,032	0,040	0,055	0,069	0,088	0,110	0,144	0,184
7,2	0,028	0,036	0,049	0,062	0,080	0,100	0,133	0,175
7,6	0,024	0,032	0,044	0,056	0,072	0,091	0,123	0,166
8	0,022	0,029	0,040	0,051	0,066	0,084	0,113	0,158
8,4	0,021	0,026	0,037	0,046	0,060	0,077	0,105	0,150
8,8	0,019	0,024	0,034	0,042	0,055	0,070	0,098	0,144
9,2	0,018	0,022	0,031	0,039	0,051	0,065	0,091	0,137
9,6	0,016	0,020	0,028	0,036	0,047	0,060	0,085	0,132
10	0,015	0,019	0,026	0,033	0,044	0,056	0,079	0,126
11	0,011	0,017	0,023	0,029	0,040	0,050	0,071	0,114
12	0,009	0,015	0,020	0,026	0,034	0,044	0,060	0,104

Примечание. Для промежуточных значений т и ЦЪ коэффициент рассеивания а определяется интерполяцией.

распределенной по прямоугольной площадке с сторонами I и Ь (1>Ь) или по кругу радиуса г. Из курса механики грунтов извест­но, что давление р с глубиной уменьшается (рассеивается) и на глубине г от уровня приложения нагрузки оно — под центром пло-шадок

р_г=ар, (И. 16)

где а — коэффициент рассеивания, определяемый по табл. 11.16 в зависимости от параметров 2г/Ь и ЦЪ, а для круга — от г/г.

Давления под углами прямоугольной площадки находят по формуле

Р_уг= 0,25ар,

но а определяют в зависимости от параметра г\Ъ.

Вертикальное давление от той же нагрузки на глубине г под любой точкой поверхности грунта легко находят по способу «угло-

45

"■} в)

в - в" в в

Я Е Л - Е

вых точек», согласно которому для вычисления давления в некото­рой точке С нужно построить четыре прямоугольника так, чтобы точка С в каждом из них была бы угловой. Тогда, по принципу не­зависимости действия сил, давление в точке С будет равно алге­браической сумме давлений в угловых точках этих прямоугольни­ков. Так, если точка С лежит внутри основного прямоугольника АВЮЕ (рис. 11.14, а), то построив прямоугольники /, //, /// и IV и находя для каждого из них в угловой точке С давления р_гс\, р_2Сп,

РгсШ И ргсгу, ПОЛуЧИМ р_2с = р_гс1 + РгсИ + ргсШ + Ргс1У. ЕСЛИ ТОЧКа С

лежит вне контура прямоугольника АВБЕ (рис. 11.14, б), то р_гс= =р2с1+р2с1у—ргсп—ргсщ (в этом случае вводятся фиктивные пло­щади // и ///).

Давление в грунте слагается из давления от собственного веса грунта и давления, передаваемого фундаментом.

Давление от собственного веса грунта называется бытовым. На рассматриваемой глубине оно равно весу вышележащего стол­ба грунта. В слоях, расположенных ниже подошвы фундамента, возникают дополнительные давления, которые и вызывают дефор­мации (осадки) грунтовой толщи. Дополнительные давления равны разности между давлением от фундамента и бытовым давлением:

Рг =ар₀=а(р — д_н), (П. 17)

где р_г — дополнительное давление на глубине, считая от подошвы фундамента; Рй — добавочное давление под подошвой фундамента; р — давление под подошвой фундамента; дн — бытовое давление на уровне подошвы фундамента.

Если р>дн, то дополнительное давление уплотняет грунты; в этом случае его часто называют уплотняющим. Если р<дн, то до­полнительное давление отрицательно и тогда оно вызывает разуп­лотнение грунта. Разуплотнение наблюдается при вскрытии глубо­ких и широких котлованов, карьеров и пр. После того, как верхний слой грунта будет удален, вскрытая поверхность, например дно котлована, не будет испытывать давления и вследствие упругих свойств грунта ее уровень несколько повысится.

Дополнительное давление может возникнуть и под подошвой существующего фундамента, если рядом с ним возводится новое сооружение, что необходимо учитывать при проектировании. В ис­кусственных сооружениях это может быть при уширении опор, при возведении нового моста рядом с существующим и т. д. Боль­шое влияние на осадки устоев оказывают насыпи земляных подхо- _ дов, если их отсыпают после возведения устоев; в таких же условиях находятся подпорные стенки. Действительно, под подошвой фун­дамента от вертикальных сил и горизонтального давления грунта

46

возникают давления по эпюре 1 (рис. 11.15, а). Если насыпь отсы­пают после постройки устоя, то от ее веса в грунте возникнут давления по эпюре 2, которые будут суммироваться с первоначаль­ными. В результате суммарные давления под подошвой будут распределены по одной из трех условных эпюр: трапецеидальной с наибольшей ординатой под передней гранью, прямоугольной и трапецеидальной с наибольшей ординатой под задней гранью. В первом случае устой получит крен в сторону пролета, во втором — осадка будет равномерная, в третьем — крен будет в сторону

насыпи.

Перечисленные виды деформаций устоев наблюдались на ряде мостов. Для их исправления требовались значительные затраты

средств.

&<

а: 5;

^{ЩЩХП^1}

Рис. 11.15. Схемы к учету веса на­сыпи

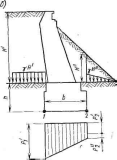
Определение дополнительных давлений, возникающих под по­дошвой фундаментов устоев от веса насыпей подходов, разработа­но А. А. Лугой. Им предложены следующие простые формулы (рис. 11.15, б):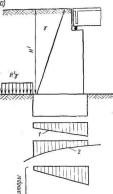

47

(Н.18в)

(II. 18г) (И.18д)

дополнительное давление от веса насыпи под задней гранью фундамента

(II. 18а)

Р\= ^И1 VII Л'!

то же, под передней гранью фундамента

р^Г2=а"₂у_иН';

(11.186)

дополнительное давление от веса конуса под передней гранью фундамента

^2= «2 Уп""-

Суммарные давления под подошвой:

2/>1 —Р1 + 'рЬ

21р2 — Ръ + р\ + р₂.

Здесь р_х, р₂, р₂— дополнительные давления, кгс/см²; -уи — вес грунта насыпи, тс/м⁸; Н' — высота насыпи, м; Я" — высота конуса, м;

^а1» ^а2 — коэффициенты по табл. 11.17; _а"—коэффициент по табл. 11.18;

2

Р\, Рг — давления под гранями фундамента без учета влияния веса насыпи.

Стабилизированные (окончательные) осадки фундаментов опре­деляют от средних давлений на грунт, вызванных нормативными нагрузками. Методом послойного суммирования осадки вычисляют в следующей последовательности.

Таблица 11.17

К 5*		Значения коэффициен­тов					эложения а А, м		сыпи Я', м	Значения коэффициен­тов
га ^			а„ нрн ширине									а при ширине
« <и	Е га о о (2	"1	подошвы, м				"5 га К к *= к га ю « ч :>>		га к о СО	*1		подошвы, м
е га 5			«5	10	15	«5						10	15
5	10 20 30	0,045 0,050 0,050	0,010 0,010	0,005 0,005	—	20		10 20 30		0,030 0,035 0,040	0,020 0,030		0,015 0,020 0,020	0,010 0,015 0,015
10	10 20 30	0,040 0,045 0,050	0,020 0,025	0,005 0,010 0,010	0,005 0,005	25		10 20 30		0,025 0,030 0,035	0,020 0,030		0,015 0,025 0,020	0,015 0,020 0,020
15	10 20 30	0,035 0,040 0,045	0,020 0,025	0,010 0,015 0,015	0,005 0,010 0,010	30		10 20 30		0,020 0,025 0,030	0,020 0,030		0,020 0,025 0,025	0,015 0,020 0,020

48

Таблица 11.18

Глубина	Значение коэффициента а при высоте насыпн Я', м				Глубина заложения фунцамента й, м		Значение коэффициента а9 при высоте насыпи Я', м
фундамента й, м	10	20	30			10		20	30
юою	0,04 0,03 0,02	0,05 0,04 0,03	0,06 0,05 0,04	20 25 30		0,01 0,00 0,00		0,02 0,01 0,00	0,03 0,02 0,01

1. Определяют среднее давление по подошве фундамента от нормативных нагрузок

2> р[ + р1 + р1 „ _п

Р=^Г + г; ^(ПЛ9)

р 2^

где ЛN — сумма вертикальных сил;

Р — площадь подошвы фундамента.

Если влияние веса насыпи не учитывают (например, при рас­чете осадок промежуточных пор моста), то последний член в фор­муле (11.19) отсутствует.

2. Строят эпюру бытовых давлений от собственного веса грун­ та (рис. 11.16).

Для этого вычисляют бытовое давление на глубине г/ от кров­ли 1-ГО СЛОЯ

1—1

Ц&АМ/ЛЩ

? ,= утг] + 2т»А- (И.20а)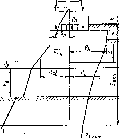

Слой I

' 1

СпойЕ

///У/////У7//////\

777777777777777777^^77777777777777^

Слой ь-ый ' УГрВ

Объемный вес водопрони­цаемого грунта определяют с учетом взвешивания его водой, а бытовое давление в водоне­проницаемых слоях по фор­муле

I—1

Я _г=УП1г'₁+'^уи1Н1+Н_ву^(11.2Щ

*| 1

Здесь \Ч11 — объемный вес 1-го слоя;

кг — мощность (толщина) 1-го слоя;

1г_в — глубина воды над водо­упорным слоем.

*1йнт

Рис. 11.16. Схема к расчету осадок фундамента методом послойного сум­мирования

3. Вычисляют дополнительное (уплотняющее) давление под подошвой фундамента: Ро=р — дн- (Н.21)

49

4. Пользуясь табл. 11.16, определяют дополнительные давления для точек, расположенных на разных глубинах г под центром по-; дошвы фундамента:

Л= РФ- (И-²²)

Дополнительные давления определяют для всех границ раздела различных слоев грунтов, а внутри каждого слоя — приблизительно . через каждые 0,4 Ь. Эпюру дополнительных давлений строят на уча­стке от подошвы фундамента до той глубины 2_акт, на которой допол­нительное давление Рж_яш составляет 20% бытового ц_гшл . Толща грунта высотой л_акт (см. рис. 11.16) называется активной зоной.

5. Вычисляют осадку фундамента, равную сжатию грунтов в пределах активной зоны:

, „ V-, Рг + Р_г^ь.

(11.23)

2Я

•Ъ=0,8 2 „„ ' А,

■ы

где

р_г — дополнительное давление на глубине г верхней границы элементарного слоя, тс/м²;

р_г+д—дополнительное давление на глубине (г+А) нижней границы элемен­тарного слоя, тс/м²; Ем — модуль деформации (-го слоя грунта, тс/м²;

Д— толщина элементарного слоя, выделенного из слоя I однородного грунта, м; 0,8 — обобщенный коэффициент, учитывающий стесненность бокового рас­ширения грунта.

Знак суммы распространяется на всю высоту 2_акт активной зоны.

Модуль деформации Ем определяют по результатам испытаний грунтов строительной площадки пробными статическими нагрузка­ми или по результатам лабораторных испытаний грунтов на сжи­маемость на приборе трехосного сжатия. В качестве ориентировоч­ных значения Еа можно принимать по табл. 11.1 и П.З.

Вычисление осадок рекомендуется производить в табличной форме:

Если в пределах активной зоны 2_акт залегает слой плотного не­сжимаемого грунта (например, скальная порода), то осадки опре­деляют с учетом ограниченной толщины сжимаемых грунтов. По

Форма

№	г	г Ь	",	Рг	Рг+Ь	Рг+Рг+\	д	Еы	Рг+Р(+&
						2			1Е
1 2

2=. .

5=0,82=

50

СИиП II-15-74 сжимаемая толщина грунта в этом случае прини­мается до кровли несжимаемого слоя, за который принимается грунт (порода) е модулем деформации /:₀=1000 кгс/см². Для фун­даментов с большой площадью основания (Ь или с?>10 м) при мо­дуле деформации грунтов ,Е₀^Ю0 кгс/см² расчетная толщина сжи­маемого слоя

Осадка 5 фундамента при конечной мощности Н сжимаемой толщи вычисляют по формуле

3=ЬрМ^ ^К1~^~¹ ■ (Н-²4)

1=1

Здесь Но, 1 — принимают равными при глинистых грунтах соответственно Эми 0,15, при песчаных — 6 м и 0,1; р — среднее давление на грунт под подошвой фундамента (без

вычета бытового давления); п — число слоев с различными Е^;

Кг — коэффициент для 1-го слоя, приведенный в табл. 11.19 и зави­сящий от параметров ЦЬ и 2г/Ь для прямоугольника н г/г для круга; М — коэффициент, учитывающий концентрацию напряжений в уров­не кровли несжимаемого слоя для пределов отношения т'=2ЩЪ или т'=Н/г:

При 0</я'^0,5 М=1,0

» 0,5<т'<1 М=0,95

» 1<т'<2 М=0,90

» 2<т'=^3 М=0,80

» 3<т'^5 .. М=0,75

Расчет осадок по методу «эквивалентного слоя» (метод Н. А. Цы-товича). Расчет осадок послойным суммированием требует доволь­но громоздких вычислений. Кроме того, он основан на ряде допуще­ний, снижающих точность определения осадок (осредненный коэф­фициент поперечной деформации грунта, условность ограничения активной зоны и пр.). Этих недостатков лишен метод «эквивалентно­го слоя», разработанный И. А. Цытовичем. «Эквивалентным слоем» называют толщу грунта, которая при нагрузке р₀, распределенной по неограниченной площади загружения (одномерная задача), дает осадку, равную осадке того же грунта, загруженного той же нагрузкой р₀, но по ограниченной площади (пространственная за­дача) .

На рис. 11.17 показана схема к расчету осадки фундамента ог­раниченных размеров и эквивалентная ей расчетная схема осадки грунта при неограниченной нагрузке. В последнем случае осадку равную осадке фундамента, определяют по простой формуле ком­прессионного сжатия

5 = П._эа₀р₀. (II. 25 )

51

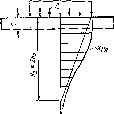
Таблица 11.19

		Коэффициент к, для фундамента
2г т= Ь		прямоугольного с соотношением сторон «=//&,
или		равным
	круглого радиусом г								ленточного
т=								при п>10
Т		1	1,4	1,8	2,4	3,2	5
0,0	0,000	0,000	0,000	0,000	0,000	0,000	0,000	0,000
0,4	0,090	0,100	0,100	0,100	0,100	0,100	0,100	0,104
0,8	0,179	0,200	0,200	0,200	0,200	0,200	0,200	0,208
1.2	0,266	0,299	0,300	0,300	0,300	0,300	0,300	0,311
1,6	0,348	0,380	0,394	0,397	0,397	0,397	0,397	0,412
2,0	0,411	0,446	0,472	0,482	0,486	0,486	0,486	0,511
2,4	0,461	0,499	0,538	0,556	0,565	0,567	0,567	0,605
2,8	0,501	0,542	0,592	0,618	0,635	0,640	0,640	0,687
3,2	0,532	0,577	0,637	0,671	0,696	0,707	0,709	0,763
3,6	0,558	0,606	0,676	0,717	0,750	0,768	0,772	0,831
4,0	0,579	0,630	0,708	0,756	0,796	0,820	0,830	0,892
4,4	0,596	0,650	0,735	0,789	0,837	0,867	0,883	0,949
4,8	0,611	0,668	0,759	0,819	0,873	0,908	0,932	1,001
5,2	0,624	0,683	0,780	0,884	0,904	0,948	0,977	1,050
5,6	0,635	0,697	0,798	0,867	0,933	0,981	1,018	1,095
6,0	0,645	0,708	0,814	0,887	0,958	1,011	1,056	1,138
6,4	0,653	0,719	0,828	0,904	0,980	1,031	1,090	1,178
6,8	0,661	0,728	0,841	0,920	1,000	1,065	1,122	1,215
7,2	0,668	0,736	0,852	0,935	1,019	1,088	1,152	1,251
7,6	0,674	0,744	0,863	0,948	1,036	1,109	1,180	1,285
8,0	0,679	0,751	0,872	0,960	1,051	1,128	1,205	1,316
8,4	0,684	0,757	0,881	0,970	1,065	1,146	1,229	1,347
8,8	0,689	0,762	0,888	0,980	1,078	1,162	1,251	1,376
9,2	0,693	0,768	0,896	0,989	1,089	1,178	1,272	1,404
9,6	0,697	0,772	0,902	0,998	1,100	1,192	1,291	1,431
10,0	0,700	0,777	0,908	1,005	1,110	1,205	1,309	1,456
11,0	0,705	0,786	0,922	1,022	1,132	1,233	1,349	1,506
12,0	0,710	0,794	0,933	1,037	1,151	1,257	1,384	1,550

\ { \	\	У'"о	\ \ \ \ \ .
\ '	{		"^
г?			-Л
:	1

Рис. 11.17. Схема к расчету осадок методом «эквивалентного слоя»

Мощность эквивалентного слоя находится по формуле Н. А. Цы-товича

Л_э =А<*>Ь

(11.26)

(1-Ю)²_

при А-

-2цо

Здесь Не — толщина эквивалентного слоя грунта, см;

Со — коэффициент относительной сжимаемости грунта, см²/кгс; Ро — добавочное (уплотняющее) давление, кгс/см²; А — коэффициент, зависящий от коэффициента Цо бокового расшире­ния грунта; е> — коэффициент, зависящий от размеров и формы подошвы фунда­мента, а также от его жесткости; Ь — ширина подошвы фундамента, см.

Для прямоугольной подошвы фундаментов со сторонами Ь и I (Ь<1) значения коэффициента Лео для абсолютно гибкого (Лсоо) и абсолютно жесткого (Лсосопзт.) фундамента приведены в табл. 11.20.

Активную зону сжатия грунта под фундаментом (см. рис. 11.17) приближенно определяют заменой криволинейной эпюры давлений в грунте треугольной с вершиной на глубине Я_акт = 2/г_а.

Осадка каждой точки при абсолютно гибком фундаменте нахо­дится способом угловых точек, полагая для угловой точки С пря­моугольника

Ао_с= 0,5А<л₀.

1,08	1,58	1,24	2,02
1,32	1,91	1,52	2,44
1,49	2,16	1,72	2,76
1,76	2,51	2,01	3,21
1,97	2,77	2,26	3,53
2,11	2,96	2,42	3,79
	3,14	—	4,00
—	3,26	—	■4,18
—	3,38	—	4,32
—	3,49	—	4,46
2,60	3,58	2,98	4,58

1 1.5

2 3 4 5 6 7 8 9 >10

1,37 1,66 1,88 2,18 2,41 2,58 2,72 2,84 2,94 3,03 3,12

1,58 1,94 2,20 2,59 2,90 3,10

3,82

Таблица 11.20

		Галька и гравий				Пески						Суглинки пластичные							Глины и суглинки
																			мигконластич-
торой		Твердые глины и суглинки											Супеси			Глины пластичные				ные
№		р.»-ОД				Но = 0,2				[%=		0,25		р.о = 0,3		Но = 0,35			а0=0,4
ошен			1				1					с			1		■■л				с
														о	(-1
&		3	э			г	8			3		3		Э		3	3
		«<	ч			ч	ч;			■ч;		Ч		Ч	■ч;	"ЧС	ч:	■Ч			«с
1,13	0,89			1,20	0,94			1,26	0,99
1,37	1,09			1,45	1,15			1,53	1,21
1,55	1,23			1,63	1,30			1,72	1,37
1,81	1,46			1,90	1,54			2,01	1,62
1,99	1,63			2,09	1,72			2,21	1,81
2,13	1,74			2,24	1,84			2,37	1,94
2,25				2,37	—			2,50	—
2,35	—			2,47	—			2,61	—
2,43	—			2,56	—			2,70	—
2,51	—			2,64	—			2,79	—
2.58	2,15			2.71	2,26			2,86	2,38

53

ю

При слоистом напластовании грунтов нужно в формулу (11.25) «место ао подставлять среднее значение коэффициента относитель-, зюй сжимаемости

1=п

лоср= ^|-1 „ (П.27)

2й;

тде кг — мощность 1-го слоя грунта в пределах активной зоны; а₀1 — коэффициент относительной сжимаемости 1-го слоя; .г* — расстояние от середины 1-го слоя до вершины треугольной эпюры уп­лотняющих давлений.

Эквивалентный слой Н_э определяют для среднего значения коэф­фициента {го-Расчет фильтрационной консолидации. При фильтрационной консолидации •осадка 5₍ за время I, считая от начала загружения грунта постоянным доба­вочным давлением, вычисляется по формуле

5,= КЗ, (11.28)

где 5 — конечная (стабилизированная) осадка уплотнения;

V — степень консолидации.

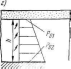
Степень консолидации зависит от физических свойств глинистого грунта, условий его загружения и условий фильтрации. Если фильтрация возможна только в нем (рис. 11.18), то в зависимости от закона распределения уплотняю­щего давления в толще глинистого грунта будут наблюдаться три случая степе­ни консолидации:

случай 0 — уплотняюшее давление постоянно по глубине (рис. 11.18, а):

^0=1-4- У! -4е-^тЗЛ\ (И.29а)

т-1,3...

случай I — уплотняющее давление распределяется по закону треугольника с «ершиной вверху (рис. 11.18, б):

а)

ГОПХ01П

■*:

в)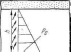

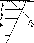
_шшшшш.

//■'У/У////У/У//У//'///// у/У/////.у//.л.. /У//

3) ^е)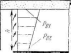

|ПП^*г
1
	1		1
•^	1		/"'
	^	--'
1	1		1 1

УУУ//УА Ш<

Рис. 11.18. Схемы к расчету фильтрационной консолидации

Значения N для этих случаев загружения и различной степени консолида­ции V приведены в табл. 11.21. Пользуясь таблицей и задаваясь величиной V, находят А' и по формуле (11.30) определяют время I, за которое грунт получит осадку 5₍. Если грунт уплотняется давлениями, изменяющимися по закону тра­пеции, то N находится по формулам:

случай 0—I при Ро1<Ро2 (рис. 11.18, г)

случай 0—II при ро1>Рог (рис. 11.18, д)

N.

ОН"

^₂ + (ЛГ₀—ЛГа)/'.

_{2 ^Н"гУ"">}

³²

т=1,3.

случай II — уплотняющее давление распределяется по закону треугольника •с вершиной внизу (рис. 11.18, в):

°° г ятя -1

'■—■=■ 2 ± .--^и '-*'" <"-²⁹">

т-1,3... I- Лт Л

ЭДри Ы= " , (11.30)

с - *^ф

ЙО'Уш,

Здесь к — толщина уплотняемого грунта, см; * — время уплотнения, с; с» — коэффициент консолидации, см²/с; Кф — коэффициент фильтрации грунта, см/с; Со — коэффициент относительной сжимаемости грунта, см²/кгс; у-иг — удельный вес воды, кгс/см³; е — основание натуральных логарифмов.

54

Значения интерполяционных коэффициентов / и /' в зависимости от отноше­ния ры/ро2 приведены в табл. 11.22.

Фильтрация воды из пор грунта возможна, если уплотняющее давление пре­высит структурную прочность грунта, а паровое давление превысит начальный градиент фильтрации. Это учитывается множителем В перед знаком X в форму­лах (П.29а)., (11.296) и (П.29в). С учетом сжимаемости поровой воды

1 В=

1 +а- «Р₀

а₀

								Таблица 11.21
	Величина ./V для случая				V		Величина ./V для случая
V	0	I	II	0			I	II
0,1	0,02	0,12	0,005	0,6		0,71		0,95	0,42
0,2	0,08	0,25	0,02	0,7		1,0		1,24	0,69
0,3	0,17	0,39	0,06	0,8		1,40		1,64	1,08
0,4	0,31	0,55	0,13	0,9		2,09		2,35	1,77
0,5	0,49	0,73	0,24	0,95		2,80		3,17	2,54

55-

									Та	блица И.2|
Рог/Роз	/	Ан/Л>01	/'	РО1/Р0*	/	Л) 1/002	/'	Рог/Рог	/	Р<н/Ро»	"
0,0	1,0	1	1,0	0,4	0,46	4	0,45	0,8	0,12	12	1 0,20 1
0,1	0,84	1,5	0,83	0,5	0,36	0	0,39	0,9	0,06	15	0,17 1
0,2	0,69	2	0,71	0,6	0,27	7	0,30	1	0,0	20	0,13 -^
0,3	0,56	3	0,55	0,7	0,19	9	0,25

при коэффициенте сжимаемости поровой воды

а_т= (1—0)

Ра

и начальном коэффициенте порового давления

Ро = 1 "

Здесь р_а — атмосферное давление, кгс/см²;

О — коэффициент водонасыщения грунта; п — пористость грунта; Ротр — структурная прочность грунта, кгс/см²;

р— давление на грунт, при котором возникает фильтрация воды,, кгс/см². Если возможна двусторонняя фильтрация воды вверх и вниз (рис. 11.18, г), то при постоянном уплотняющем давлении вместо мощности И, сжимаемого слоя. нужно подставить величину 0,5й и расчет вести по случаю 0. При внешней уп-'-лотняющей нагрузке, расположенной по площади прямоугольника (рис. 11.19), что соответствует воздействию фундаментов, к приравнивается активной зоне, равной 2к_э, где к_а— эквивалентный слой грунта, определяемый по формуле (11.26).

В зависимости от напластования грунтов будем иметь при этом следующие возможные случаи.

Толща глинистого грунта превышает (или равна) активную зону, фильтра­ция воды только вверх (рис. 11.19, а), расчет ведется по случаю II при к—к₃;

толща глинистого грунта равна активной зоне, фильтрация воды вверх и вниз (рис. 11.19, б), расчет ведется по случаю 0 при к=к_э;

толща глинистого грунта меньше активной зоны, фильтрация воды вверх и вниз (рис. 11.19, в), расчет ведется по случаю 0—II при 0,5/г_э;

толща глинистого грунта меньше активной зоны, фильтрация воды только вверх (рис. 11.19, г), расчет ведется по случаю 0—II при к=к_тп.

В) /	и \ и
,	♦		/
•ч	А		./
<~ч1	т		у
II			И
" 1 >		{■■
		•,;.:/;■
?4 а		/:
		Ьууу^		'-"■

а)

	1 | |г " у
	I
<Х1 II	*
-%	т
1
	' ' УУУ,	УУУ/УУУШУ/

Расчет осадок с учетом ползучести грунтов. Протекание осадок фундаментов во времени зависит не только от выжимания воды из пор грунта, но также и от его ползучести. Ползучесть присуща глинистым грунтам. При твердой и полу­твердой их консистенции осадки ползучести могут превышать фильтрационные

осадки в 1,5—2 раза.

Ползучесть возникает при давлениях на грунт, превышающих его структурную прочность, когда жесткие связи между его частицами оказываются разрушенны­ми. В начальный период в фазе неустановившейся ползучести, деформации на­растают относительно быстро главным образом за счет все большего разрушения структурных связей и закрытия имеющихся в грунте микротрещин. Далее насту­пает фаза установившейся ползучести. В этой фазе происходит сложный процесс постепенного разрушения водноколлоидных связей с одновременным образова­нием новых. Если разрушение этих связей опережает образование новых, то деформации ползучести не затухают и переходят в прогрессирующую ползучесть. В противном случае деформации ползучести постепенно затухают и прекраща­ются. Прогрессирующая ползучесть грунтов оснований недопустима, так как приводит к полному разрушению сооружения.

Многочисленные экспериментальные исследования показывают, что объемной ползучести глинистых грунтов, вызывающей осадки фундаментов, в наибольшей степени соответствует модель линейной наследственной ползучести Болышана — Вольтерра. Согласно этой модели осадка грунта при безграничном в плане нагру-жении (одномерная задача)

5,= /шо[\ + -^-(1-е-⁶>')^,

где к — мощность сжимаемой толщи;

р — равномерно распределенное внешнее давление;

Со' — относительный коэффициент первичной консолидации при р=1; • 6,61 — параметры ползучести, определяемые специальными опытными иссле­дованиями образцов грунта.

При действии местной нагрузки (пространственная задача) к=к,_в.

В общем случае осадка глинистого грунта зависит как от ползучести, так и от фильтрационной консолидации. Решение этой задачи получено школой Н. А. Цытовича (Ю. К. Зарецким и др.) в рядах, аналогичных фильтрационной консолидации. Для практических целей достаточно принять первые члены рядов. Тогда осадка 5<, накопленная за время I от начала загружения, выразится

следующими формулами:

при двусторонней фильтрации и треугольной эпюре уплотняющих давлений

(см. рис. 11.19, б);

8 _ш ъ Г , , 8»1 еГ^ш — е~⁸¹' 1 1—В—~е~^т +— В 1 — е^_м -•

^Х • »1+В ^:

при односторонней фильтрации вверх и треугольной эпюре уплотняющих давлений (см. рис. 11.19, а)

5( = й_эа₀/>₀&1 X

16 / 2 \ _ш Ъ „ Г . < 16»! / 2 \ _е—М'__е-М 1 1 ~-В 1 ■■ )е~^ш + В 1 — е~^м— ——- 1 — — —

при М = —-в- ,

Рис. 11.19. Схемы к расчету фильтрационной консолидации при ограниченном загружении

56

Обозначения прежние.

57

Расчет деформаций смещения. Наблюдения за подпорными стенами, устоями мостов и другими аналогичными сооружениями, подверженными односторонним, постоянно действующим горизонтальным сдвигающим силам (например, давле-' нию земли), показывают, что при основаниях, сложенных глинистыми грунтами, при некоторых условиях в этих сооружениях возникают длительные деформации смещения (горизонтальные сдвиги). Причина этих деформаций — ползучесть глин-яод действием касательных напряжений. Исследование этого явления и разра­ботка инженерного метода расчета сооружений на ползучесть сдвига было вы­полнено Н. Н. Масловым и его учениками.

Так же как и объемная, ползучесть сдвига может быть неустановившейся, установившейся, затухающей и прогрессирующей. Прогрессирующая ползучесть. недопустима, так как приводит к полному разрушению сооружения. Допусти­мость затухающей ползучести определяется величиной конечных деформаций и скоростью их протекания и зависит от назначения конкретного сооружения.

Ползучесть сдвига находится в прямой зависимости от прочности глинистых грунтов на сдвиг:

Три>= Рп ¹ЁЧш + 2л» + Со

где Три — сопротивление грунта сдвигу;

ф_и — истинный угол внутреннего трения грунта; р_п — нормальное к площадке сдвига напряжение; 2_И — водно-коллоидные связи грунта; с_с — структурное (жесткое) сцепление. Все величины в этой формуле, кроме с_с, зависят от влажности грунта V? <что подчеркивается индексом те в ее написании). Если сдвигающее напряжение меньше х_тк, т. е.

то деформации сдвига отсутствуют. Но если будут преодолены силы трения и структурное сцепление, то в рассматриваемой точке возникнет ползучесть, об­условливаемая водно-коллоидными связями. Таким образом отсутствие деформа­ций ползучести может быть записано в виде

Ъ < *11т= РпЧЧчи + Сс,

где Тит — названа Н. Н. Масловым «порогом ползучести».

Характер протекания ползучести во времени зависит от водно-коллоидных связей 2ш грунта. Водно-коллоидным связям присущи свойства вязкости. Вяз­кость измеряется коэффициентом вязкости т), зависящим от свойств вязкого тела и условий протекания вязкого течения. Для глинистых грунтов коэффициент вязкости зависит тоже от времени действия сдвигающего давления. Эксперимен­тами установлено, что при затухающей ползучести коэффициент вязкости в момент времени ( от начала загружеиия

%=%-(%-ЧоГ*¹'- (Н-31)

где т]₀—начальная вязкость при <=0; т]н — конечная вязкость при (= со; ц — параметр, зависящий от природных свойств глинистого грунта. Величины вязкости * находят специальными испытаниями образцов грунта в лабораторных условиях. Для предварительных расчетов значения т] можно принимать по табл. 11.23.

Зная т], параметр ц можно найти, логарифмируя выражение (11.31):

1 . % —Чо * Чк —К

Рассматривая задачу в плоской постановке и прикладывая к подошве фун­дамента шириной Ь и длиной, равной единице, горизонтальные касательные рав-

¹ Единица динамической вязкости — пуаз; 1 пз = 1 кгс-с/м² (килограмм-сила» секунда на квадратный метр).

58

Таблица 11.23"

	Коэффициент вязкости, из			Консистенция гли­нистого грунта	Коэффициент вязкрсти, пЕ>
Консистенция гли­нистого грунта	Чо	1к	1о		%
Мягопластичная Тугопластичная	в 1010 в10«	аЮ12 а 1013	Полутвердая Твердая		а 1014 а 10«	«1015 аЮГ7

Примечание. Коэффициент а=1 -5-9.

иомерно распределенные усилия д₀ (рис. 11.20), Н. Н. Маслов получил выраже­ние для горизонтального смещения подошвы фундамента:

X

_{ь-^^^ННИ^Н}}

}■

Ы

1 , % — (%— Чо) ^

■По

где р — вертикальное давление на грунт по подошве фундамента; у — объемный вес грунта;

О — активная зона (толща) грунта, подвергающаяся деформациям ползу­чести. Активная зона представляет ту толщу грунта, в которой касательные на­пряжения превышают порог ползучести. Из этого положения определяется вели­чина И. Приравнивая касательные напряжения под осью фундамента на глуби­не г порогу ползучести, получим

_У

_^{

* 2Ьг

У/кУ/АУ/АУ/АУ/Ау/^.

Рис. 11.21. График к определению ак­тивной зоны

59

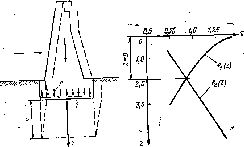
2* 4г2 + №

агс1°;

Рис. 11.20. Схема к расчету ползуче­сти сдвига

(р + уг)18<еъ, + ^сс-

Значение г удовлетворяющее этому равенству, и будет равно толщине й активной зоны. Решать эти уравнения проще всего графически, строя кривую

/1(2)= аг с1д ——

я I 2г 4г2 + Ь2)

и прямую

/2 (г) = (р + V*) 1§«(>«, + с_с.

Точка пересечения этих функций дает ординату г=й (рис. 11.21) Для предварительных расчетов можно принимать /?=0 56 Расчет просадок просадочных грунтов. Как указывалось," просадочным грун­там свойственны при замачивании просадки. По данным опытов величина отно­сительной просадки, определяемая формулой (И.7), зависит от давления р на рассматриваемый слой грунта. Давление р должно быть при этом больше на­чального просадочного давления р_пр. Так как в толще грунта давления не по­стоянны (от собственного веса они с глубиной возрастают, а от давления фун­дамента уменьшаются), то для расчета просадок необходимо в лабораторных условиях найти зависимость б_пр от внешнего давления р. Эту зависимость нахо­дят, испытывая образцы грунта ненарушенной структуры, при заданном давле­нии с последующим замачиванием до полного водонасыщения. Определив затем давление р,- на 1-й слой грунта от его веса и внешней нагрузки, передаваемой фундаментом, находят 6_пр< по формуле (11.7) и далее искомую величину про-

⁵11р = 2Хф/Л₍-т, (11.32)

где Нг — толщина 1-го слоя грунта;

т — коэффициент условия работы, принимаемый для фундаментов шириной 12 м и более, равным 1, а для ленточных фундаментов шириной до 3 м и прямоугольных шириной не более 5 м по формуле

т=0,5+1,5(/7 —^р), (11.33)

где р — среднее давление по подошве фундамента кгс/см² (р_Пр — то же в кгс/см², так как коэффициент 1,5 имеет размерность см²/кгс).

При других размерах фундаментов коэффициент т находят интерполяцией между 1 и значением, определенным по формуле (11.33).

При вычислении 5_пр знак 2 распространяется на всю просадочную толщу, нижней границей которой служит условие бпр=0,1.

Расчет креиов. Крен фундаментов наблюдается в двух случаях:

1. На подошву фундамента действует вертикальная сила, приложенная на расстояние е от центральной оси, и создающая, следовательно, момент Л1=#е. В результате под подошвой возникают неравномерные давления на грунт и фун­дамент оседает больше той гранью, под которой напряжения больше.

2. Грунты под фундаментом неоднородны по сжимаемости.- При таком на­пластовании грунтов крен может возникнуть и при центрально приложенной внешней силе N в сторону более слабого грунта. Крен измеряется тангенсом угла наклона.

При мелком заложении в однородных грунтах крен фундамента с прямо­угольной подошвой определяется по формулам: в направлении большей стороны подошвы /

1 — ц2 №е_г Н=—р т——;

в направлении меньшей стороны подошвы в Ь

1—И² Ше_ь ¹ь — —~ кь'

63

60

Таблица 11.24

Отношение сторон прямо­угольника	к1	КЬ	Отношение сторон прямо­угольника	к1	КЬ	Отношение сторон прямо­угольника	к1	кь
1,0 1,4	0,5 0,71	0,5 0,39	1,8 2,4	0,83 0,97	0,33 .0,25	3,2 1.5,0	1,10 1,44	0,19 0,13

где еь е_ь — эксцентриситет приложения силы N соответственно вдоль стороны /и Ь; Кь к_ь — коэффициенты, зависящие от отношения сторон и приведенные в

табл. 11.24; Ей, ц — средние по сжимаемой толще модуль деформации и коэффициент

Пуассона грунта. Под сжимающей толщей понимают активную зону сжатия грунта при дей­ствии силы N.

Для фундамента с круглой подошвой крен

1 —1*2 Ые

где е — эксцентриситет силы Л?;

г — радиус подошвы фундамента;

к, — коэффициент, зависящей от отношения г к толщине Н активной зоны сжатия:

Ш . . 0,25 0,5 1,0 2,0 >2,0

Кг 0,26 0,43 0,63 0,74 0,75

Если напластование грунтов под фундаментом неоднородное, то крен может быть вычислен по осадкам его граней. Так, крен фундамента прямоугольной по­дошвы в направлении стороны Ь будет

5] — 5о

I =

где $_ь 5₂ — осадки середин противоположных граней фундамента, определяв' мые способом угловых точек.