Глава VIII. Несущая способность свай

УШ.1. ОБЩИЕ СВЕДЕНИЯ

Несущая способность сваи — наибольшее силовое воздействие, которое может воспринять свая, — зависит от прочности (трещи-ностойкости) материала сваи и несущей способности грунтов, в ко­торые она погружена.

Несущая способность по материалу определяется расчетом прочности и трещиностойкости сваи при действии на нее продоль­ных и поперечных сил и изгибающих моментов. Эти расчеты вы­полняют по правилам расчета строительных конструкций, изучае­мых в соответствующих курсах.

Несущая способность Ф сваи по грунту при действии централь­но приложенной вдавливающей силы слагается из сопротивления грунта Ф_н под ее нижним концом и сопротивлением грунта Фб по боковой поверхности сваи, т. е.

_Ф=Ф_{Н +} Ф₆. (УШ.1)

В уровне торца сваи сопротивление грунта под нижним кон­цом сваи и боковое сопротивление распределяются по площади круга радиуса (1-=-4)й, где й — толщина сваи (рис. VIII.1, о). В расчетах схему давления на грунт упрощают и при расчетах не­сущей способности сваи сопротивление под нижним концом прини­мают равномерно распределенным по площади торца сваи (рис.

хпы.б).

В висячих сваях сопротивление грунта под торцом зависит от способа погружения сваи. В забивных сваях под их торцом обра­зуется ядро из уплотненного грунта, как бы увеличивающее пло­щадь опирания сваи на грунт. Размеры ядра не поддаются точному определенно — их учитывают увеличением расчетных сопротивле­ний под торцом забивной сваи. В сваях-оболочках, погружае­мых с извлечением грунта из их полости, а тем более в буровых сваях уплотненное ядро «е образуется и грунт в уровне их опира­ния существенно не изменяет своего природного сложения.

Очевидно, чем плотнее грунт, тем больше величина сопротив­ления грунта под нижним концом сваи, которое в надежно погру­женной свае составляет 60—70% всей несущей способности.

Боковое сопротивление возникает между грунтом и прочно свя­занной с поверхностью сваи «грунтовой рубашкой» (толщина 1— 2 см). Этим объясняется, что боковое сопротивление практически не зависит от материала сваи. Оно слагается из внутреннего тре­ния грунта, пропорционального нормальному давлению на данной глубине, и сил сцепления. Так как нормальное к поверхности сваи давление грунта с глубиной увеличивается, то и трение с глубиной

232

возрастает. Боковое сопротивле­ние также зависит от вида свай: при забивных сваях, когда окру­жающий грунт уплотняется, тре­ние больше.

Рис. VIII.1. Схемы передачи сваей нагрузки грунту

Как показывают исследова­ния, при постепенном нагружении сваи сначала развивается сопро­тивление грунта под ее торцом и лишь после осадки головы сваи на несколько миллиметров проис­ходит срыв сцепления и по по­верхности сваи развивается со­противление, обусловленное пре­имущественно величиной внутрен­него трения грунта. При опирании сваи на несжимаемый грунт, на­пример, скалу, осадка сваи отсут­ствует и тогда боковое сопротивление не учитывается (Фб = 0).

Боковое сопротивление может быть положительным и отрица­тельным. При вдавливающей нагрузке положительное сопротивле­ние направлено снизу вверх, в сторону, противоположную дейст­вия нагрузки, и увеличивает несущую способность сваи. Отрица­тельное сопротивление возникает, когда окружающий грунт по тем или иным причинам смещается вниз по отношению к погруженной свае. Такое смещение наблюдается, если пригрузить поверхность грунта дополнительной нагрузкой, например насыпью у устья мо­ста, а также, когда в толще грунта имеются слои легкосжимаемых грунтов, например торфа. Во всех этих условиях грунт зависает на свае и дополнительно нагружает ее.

Кроме вдавливающей продольной нагрузки, на сваю может действовать выдергивающая сила. Несущая способность сваи в этом случае создается только боковым сопротивлением грунта и определяется формулой

Ф_в= Фб. (VIII. 2)

где Ф_ъ — несущая способность сваи на выдергивание.

В сваях с уширенным нижним концом выдергивания сопротив­ляется также грунт, расположенный над уширением. Однако рабо­та сваи в этих условиях изучена еще недостаточно, и поэтому в расчетах сопротивление грунта над уширением не учитывают.

При поперечных (горизонтальных) нагрузках сваю рассматри­вают как стержень той или иной жесткости, погруженный в упру­гую среду — грунт. Так как горизонтальные перемещения фунда­ментов ограничены (1—3 см), то представляется возможным грунт рассматривать как среду с линейной зависимостью между ее со­противлением и перемещением в рассматриваемом уровне. За пре­дельное сопротивление грунта при этом принимается его пассив­ный отпор по теории Кулона.

233

9—2644

В фундаментах располагают, как правило, большое число свай, достигающее несколько десятков. Группу свай в фундаменте принято называть «кустом».

В кусте сваи располагают на расстоянии между осями в две-три их толщины (см. п. У1.5). При таком расстоянии напряженные зоны грунта вокруг свай накладываются друг на друга и давление на грунт в уровне нижних концов свай возрастает по сравнению с одиночной сваей (рис. УШ.2). Суммарные давления на грунт, передаваемые кустом свай, не должны превышать расчетных со­противлений грунтов в основании свайного фундамента как еди­ного грунто-свайного массива.

а)

ШШШШ

Суммарные давления под торцами свай создают напряженное состояние грунта, определяющее осадку фундамента. Осадка будет тем больше, чем больше добавочное давление под сваями и чем больше размеры фундамента в плане, т. е. чем больше число свай в кусте. Осадка куста всегда больше осадки одиночной сваи, так как активная зона грунта под одиночной сваей всегда меньше ак­тивной зоны под кустом свай. При расчетах свайных фун­даментов исходят из несущей способности по грунту отделы ной сваи в кусте и несущей способности всего куста свай, рассматривая последний как фундамент глубокого заложе­ния (см. п. 1Х.4).

*\т*

Несущая способность сваи по грунту Ф определяется ана­литическим методом и испыта­ниями свай в грунтовых усло­виях строительной площадки. Все большее применение нахо­дит зондирование грунтов, с помощью которого достаточно достоверно находят сопротив­ления грунта в уровне нижних концов свай и по их боковым поверхностям.

Рис. У111.2. Схемы работы свайных

фундаментов:

а — напряженная зона под кустом свай;

б — активная зона под кустом свай; в —

активная зона под одиночной сваей

Испытанию подвергают от­дельные сваи в соответствии с требованиями ГОСТ 5686—78. В результате испытания нахо­дят нормативное предельное сопротивление сваи Ф*_Р- Несу­щая способность сваи в фун­даменте

Ф = т

234

(УШ.З>

где т — коэффициент условия работы, равный 1,0 при испытании вдавливаю­щей или горизонтальной нагрузкой и равный 0,8 — при выдергиваю-' щей нагрузке;

Ф" — нормативное предельное сопротивление сваи; к_г — коэффициент запаса по грунту.

Если испытывают в одинаковых грунтовых условиях менее ше­сти свай, то нормативное предельное сопротивление принима­ют равным наименьшему предельному сопротивлению, получен­ному при испытании свай, т. е.Ф"_р = Ф_нр._т!п ^и коэффициент /с_г= 1. Если испытывают шесть или более свай, то ^ф„_р. ^{и к}г находят пу­тем статистической обработки частных значений предельных сопротивлений Ф_Пр свай (по ГОСТ 20522—75), полученных при ис­пытаниях (см. п. VIII.3).

У1Н.2. АНАЛИТИЧЕСКИЙ МЕТОД ОПРЕДЕЛЕНИЯ НЕСУЩЕЙ СПОСОБНОСТИ СВАЙ

Аналитический метод определения несущей способности свай по грунту основан на большом числе испытаний сваи в различных грунтовых условиях и определения (на основе анализа) сопротив­лений грунта под торцом и по боковой поверхности свай. В этом направлении была проведена большая работа д-ром техн. наук А. А. Лугой.

По аналитическому методу сопротивление грунта под нижним концом и по боковой поверхности сваи рассматривают независимо друг от друга, что позволяет суммировать их и выражать несущую способность сваи формулами, аналогичными по построению фор­муле (VIII.!). Такой подход к решению этой задачи принят в боль­шинстве стран. Ниже излагается метод, принятый в СССР и осно­ванный на теории расчета сооружений по предельным состояниям.

Несущая способность сваи по грунту зависит от вида сваи и грунтов, в которые она погружена.

При опирании свай на практически несжимаемые грунты

Ф = тПР, (VIII.4)

где т — коэффициент условия работы, принимаемый равным 1,0;

Я. — расчетное сопротивление грунта под нижним концом сваи, тс/м³;

Р— площадь опирания сваи на грунт, принимаемая: для свай сплошного сечения и полых с закрытым нижним концом равной площади попереч­ного сечения сваи (по наружному контуру); для полых свай с откры­тым нижним концом и свай-оболочек равной площади сечения стенок; для полых свай и свай-оболочек, если их полости заполнены внизу бе­тоном на высоту не менее трех диаметров сваи (оболочки), полной площади поперечного сечения (по наружному контуру), м².

9*

Для забивных свай всех видов, опирающихся на скальную не­разрушенную выветриванием породу, крупнообломочные грунты с песчаным заполнением или глинистые грунты твердой консистен-

235

ции, 7? = 2000 тс/см². Для свай-оболочек, равномерно опираемых на прочную скальную породу, прикрытую слоем неразмываемого грунта толщиной не менее трех диаметров оболочки,

Л=——. (УШ.5)

Для буронабивных свай, свай-оболочек и свай-столбов, заде­ланных в невыветренную скальную породу на глубину не менее 0,5 м,

д=-^-(4- + ¹4 (Утл)

Здесь Я"_ж— нормативное значение временного сопротивления скальной породы в водонасыщенном состоянии на одноосное сжатие, тс/м²; /с_г — коэффициент запаса по грунту, равный 1,4; Аз — глубина заделки, м; из — диаметр заделанной части сваи, м.

Формула (УШ.6) основана на экспериментальных исследова­ниях.

При других грунтовых условиях — сильно трещиноватой или вы-ветрелой породы, породы с прослойками нескальных грунтов и прочих — нормативное сопротивление ^ сие определяют штамповы-ми испытаниями грунтов или испытаниями опытных свай статиче­ской нагрузкой.

Несущая способность забивных висячих свай (свай, по­груженных в-сжимаемые грунты) толщиной не более 0,8 м на осе­вую вдавливающую нагрузку

Ф = т(т_н ЯГ+ 11% яу |1|), (VIII. 7)

где т — коэффициент условия работы, принимаемый равным I;

Н — расчетное сопротивление грунта под нижним концом сваи

(табл. УШ.1), тс/м²; Г — площадь поперечного сечения сваи (по наружному контуру), а при

камуфлетном уширении площади поперечного сечения уширеиия по

его наибольшему диаметру, м²; и — наружный периметр поперечного сечения сваи, м; /ч — расчетное сопротивление 1-го слоя грунта по боковой поверхности

сваи (табл. УШ.2), тс/м²; и — толщина 1-го слоя грунта, м; Ив, Ш{ — коэффициенты условия работы грунта соответственно под нижним

концом и по боковой поверхности сваи (табл. УШ.З).

Коэффициенты условия работы т_г и т/ учитывают независимо друг от друга и перемножают. Так, например, для полой сваи с диаметром полости более 40 см, погруженной в суглинки вибропо­гружателем;

^=0,8-0,7=0,56;

«/=0,9- 1 = 0,9. 236

Таблица УШ.1

			1есчаные грунты средней плотности
Глубина погружения нижнего конца	граве-листые	крупные	-	средней крупности	мелкие	пылеватые	-
		Глинистые грунты с показателем консистенции /,
	0	ОД	0,2	0,3	0,4	0,5	0,6
			Расчетные сопротивления У?, тс/м"
3	750	660 400	300	310 200	200 120	ПО	60
4	830	680 510	380	320 250	210 160	125	70
5	880	700 . 620	400	340 280	220 200	130	80
7	970	730 690	430	370 330	240 220	140	85
10	1050	770 730	500	400 350	260 240	150	90
15	1170	820 750	560	440 400	290	165	100
20	1260	850	620	480 450	320	180	ПО
25	1340	900	680	520	350	195	120
зо-	1420	950	740	560	380	210	130
35	1500	1000	800	600	410	225	140

Примечания. I. Для значений К, указанных дробью, числитель относится к пес­кам, знаменатель к глинам.

2. Для плотных песчаных грунтов, плотность которых определена статическим зонди­рованием, значение К для свай, погруженных без подмыва или лидерных скважин, увели­чиваете» в 2 раза, а при отсутствии зондирования в 1,6 раза, но не более чем до 2000 тс/м^!.

Глубину расположения нижнего конца сваи для определения -К {см. табл. VIII.1) и глубину расположения середины 1-го слоя грун­та для определения /_г- (см. табл. \^111.2) принимают от дна водо­тока после общего размыва при расчетном паводке, а на сухой ме­стности (суходолах и пр.) от уровня природного рельефа, если срезка, подсыпка или намыв территории не превышают 3 м (рис. VIП.З, а); если же срезка, подсыпка или намыв составляют от 3 до Юм, то принимают от условного уровня, расположенного соот­ветственно на 3 м выше уровня срезки или на 3 м ниже уровня под­сыпки (рис. УШ.З, б).

237

Таблица УШ.2

Средняя глубина

располо­жения слоя грунта, м

Песчаные грунты средней плотности

крупные я средней крупности	мелкие	пылеватые	-	-	-	-	-		-
	Глинистые группы с показателем коилкле-щим ^.
0,2	0,3	0,4	0,5	0,6	1л7	0 Л	0 )		1.0

0,2 0,4 0,5 0,5 0,6 0,6 0,6 0,6 0,6 0,6 0,6 0,7 0,7

3,5 4,2 4,8 5,3 5,6 5,8 6,2 6,5 7,2 7,9 8,6 9,3 10,0

2,3 3,0 3,5 3,8 4,0 4,2 4,4 4,6 5,1 5,6 6,1 6,6 7,0

1 2 3 4 5 6 8

10 15 20 25 30 35

1,5 2,1 2,5 2,7 2,9 3,1 3,3 3,4 3,8 4,1 4,4 4,7 5,0

Расчетное сопротивление /- на боковой поверхности свай и свай-оболочек тс/ь

1,2	0,8	0,4	0 4	0,3
1,7	1,2	0,7	0,5	0,4
2,0	1,4	0,8	0,7	0,6
2,2	1,6	0,9	0,8	0,7
2,4	1,7	1,0	0,8	0,7
2,5	1,8	1,0	0,8	0,7
2,6	1,9	1,0	0,8	0,7
2,7	1,9	1,0	0,8	0,7
2,8	2,0	1,1	0,8	0,7
3,0	2,0	1,2	0,8	0,7
- 3,2	2,0	1,2	0,8	0,7
3,4	2,1	1,2	0,9	0,8
3,6	2,2	1,3	0,9	0,8

Примечание. Расчетные сопротивления \^ для плотных песчаных грунтов нужно увеличивать на 30%-

Сопротивление /* находят для середин однородных слоев грунта толщиной не более 2 м и суммируют по всей толщине грунтов, прой­денных сваей.

Если в пределах погружения сваи имеются слои торфа толщи­ной более 0,3 м и возможна подсыпка территории или иная ее загрузка, то значения /* для грунтов, расположенных выше подош­вы наинизшего слоя торфа, принимают: при подсыпке до 2 м — для грунтов подсыпки и торфа равными нулю, а для минеральных пла­стов природного грунта — положительным значениям по табл. УШ.2; при подсыпках от 2 до 5 м — для минеральных пластов при­родного грунта и подсыпки значениям по табл. VIII.2 с коэффици­ентом минус 0,4 тс/м², а для торфа — минус 0,5 тс/м²; при подсып­ках более 5 м для минеральных пластов природного грунта и под­сыпки— по табл. УШ.2 со знаком минус, а для торфа — минус 0,5 тс/м².

Несущую способность буровых свай (набивных и буро-опускных) и свай-оболочек, опирающихся на сжи­маемые грунты, определяют с учетом'некоторого разуплотне­ния грунтов, так как их изготавливают с удалением грунта из сква­жины или полостей оболочек. Несущую способность таких свай тоже находят по формуле (УП1.7), но с следующими значениями входящих в нее величин.

238

а) В)		п
"1			щ
			ш		«1
	\<*\^<ХЧк
	«Г	1
0;		~~'■
	-с

^т

Коэффициент т условия рабо­ты принимают равным 0,8 при опирании сваи на покровные гли­нистые грунты со степенью влаж­ности С>0,85 и на просадочные грунты, а в остальных случаях т=\. Коэффициент условия ра­боты т_н принимают равным 1 во всех случаях, кроме свай с каму­флетным уширением, для которых <я_л=1,3, и свай с уширенной пя­той, бетонируемой подводным способом, для которых т_л=0,9.

Рис. УШ.З, Схемы к расчету несу» шей способности сваи по грунту

			Таб	лица	У1И.З
	Коэффициент			Коэффициент
	условия	работы		условия	работы
Способы погружения свай			Способы погружения свай и вицы грунтов	грунта
и виды грунтов
	тп	т *		тн	"7
Погружение забивкой	1.0	1,0	Вибропогружение в
сплошных и полых с за-			глинистые грунты с по-
крытым концом свай ме-			казателем консистенции
ханическими, паровоз-			/ь=0,5:
душными и дизельными			супеси	0,9	0,9
молотами			суглинки	0,8	0,9
Погружение забивкой	1,0	0,5	глины	0,7	0,9
в лидерные скважины с			То же, в глинистые с	1,0	1.0
последующим заглуб-			показателем консистен-
лением ниже забоя сква-			ции /ь=^0
жины не менее 1 м при			Погружение забивкой		■ >
диаметре скважины, рав-			любыми молотами по-		V
ном стороне квадратной			лых свай с открытым
сваи			нижним концом при диа-
То же, на 5 см мень-	1,0	0,6	метре полости:
шем стороны квадратной			40 см и менее	1.0	1.0
сваи			более 40 см	0,7	1.0
Погружение с подмы-	1,0	0,9	Сваи с камуфлетным
вом в песчаные грунты с			уширением и а глубине
добивкой сваи без под-			10 м и более в песчаных
мыва на последнем, мет-			грунтах средней плотно-
ре погружения			сти и в глинистых грун-
Вибропогружение в			тах консистенции 1ь^
пески средней плотности:			^0,5 при диаметре уши-
крупные и средней	1,2	1,0	рения:
крупности			1,0 м независимо от	0,9	1,0
мелкие	1,1	1,0	грунтов
пылеватые	1.0	1,0	1,5 м в песках и су­песях	0,8	1,0
			1,5 м в суглинках и	0,7	1.0
			глинах

Примечание. Коэффициенты т^ и т* при вибропогруженни в глинистые грунты консистенции 0,5>/,>0 определяются интерполяцией.

Таблица УШ.4

	Коэффициент		т* условия работы
Вид и способ устройства свай
	Песок'	Супеси	Суглинок	Глина
Буронабивные бетонируемые:
при отсутствии воды в скважине	0.7	0,7	0,7	0.6
под водой или глинистым рас-	0,6	0,6	0,6	0,6
твором
Сваи-оболочки, погружаемые ви-	1,0	0,9	0,7	0,6
брированием с выемкой грунта
Сваи-столбы	0,7	0,7	0,7	0,6

Коэффициент условия работы т^ принимают по табл. УШ.4. Площадь Р опирания сваи принимают равной: для свай-столбов и свай без уширения нижнего конца — площади поперечного сече­ния сваи; для свай с уширением (пятой) — площади поперечного сечения уширения по его наибольшему диаметру; для свай-оболо­чек, заполненных бетоном,— площади поперечного сечения оболоч­ки (по наружному контуру); для свай-оболочек с грунтовым ядром без бетонного заполнения полости оболочки — площади поперечно­го сечения стенок.

Периметр и принимают равным периметру скважины, обсадной трубы или сваи-оболочки. Расчетное сопротивление /; принимают по табл. УШ.2; при этом для столбов с уширенной пятой сопротив­ление и в несвязных грунтах учитывают только на участке от верха столба до уровня пересече­ния поверхности столба с поверхностью вообра» жаемого конуса, построенного на уширении как на диаметре с образующей наклонной к оси стол­ба под углом 0,5 <р1, где ф1 — среднеарифметиче­ское расчетное (по первому предельному состоя» нию) значение угла внутреннего трения грунтов, залегающих в пределах конуса (рис. УШ.4). В связных грунтах сопротивление и учитывают по всей длине столба.

Расчетное сопротивление К грунта в основа­нии бурового (набивного и буроопускного) стол­ба без уширения или с уширением и сваи-обо­лочки, погруженной с удалением грунта из ее полости и последующим заполнением нижней части полости бетоном на высоту не менее трех ее диаметров, принимают равным следующим ве­личинам:

при опирании на крупнообломочные грунты с песчаным заполнением и на песчаные грунты бу­ хучету бокового рового столба и оболочки, погруженной с удале- сопротивления нием грунта до ее ножа,

свай (столбов) с _& . _й/₊ ^ [(УШ.8а>

уширенной пятой " ">^'г«1^млкт»11» _к;* »л '

240

а в случае оболочки, погруженной с сохранением внизу ненарушем ного ядра грунта высотой не менее 0,5 м,

К = р (V; аА°_к + а_У1кВ°_к), (VIII. 86)

где а, р, А_к и В_к — безразмерные коэффициенты, принимаемые по табл. УШ.5 в зависимости от расчетного значения угла внутреннего трения ({)1 грунта основания; VI — расчетный объемный вес грунта основания с учетом взве­шивания в воде, тс/м²; VI—осредненный по слоям расчетный вес грунтов, располо­женных выше нижнего конца столба (его уширения) или оболочки, тс/м³; й — диаметр столба или его уширения, м;

И — глубина заложения нижнего конца столба или его уши­рения, считая от природного рельефа или отметки срез­ки, а в русле рек—от дна с учетом его общего размыва при расчетном паводке, м. Формулы (УШ.8) исходят из предельного состояния несвязных грунтов, нагруженных равномерно вертикальной нагрузкой.

При опирании буронабивной или буроопускной сваи с ушире­нием и без уширения, а также сваи-оболочки с заполненной поло­стью бетоном на глинистые грунты расчетное сопротивление при-

Таблица УШ.5

Обозначение коэффициента	Н й	Расчетный угол внутреннего трения <р , град
		23	25	27	29	81	33	35	37	39
А0	—	9,5	12,6	17,3	24,4	34,6	48,6	71,3	108,0	163,0
п° Вк	—	18,6	24,8	32,8	45,5	64,0	87,6	127,0	185,0	260,0

а	4	0,78	0,79	0,80	0,82	0,84	0,85	0,85	0,86	0,87
а	5	0,75	0,76	0,77	0,79	0,81	0,82	0,83	0,84	0,85
а	7,5	0,68	0,70	0,71	0,74	0,76	0,78	0,80	0,82	0,84
а	10	0,62	0,65	0,67	0,70	0,73	0,75	0,77	0,79	0,81
а	12,5	0,58	0,61	0,63	0,67	0,70	0,73	0,75	0,78	0,80
а	15	0,55	0,58	0,61	0,65	0,68	0,71	0,73	0,76	0,79
а	17,5	0,51	0,55	0,58	0,62	0,66	0,69	0,72	0,75	0,78
а	20	0,49	0,53	0,57	0,61	0,65	0,68	0,72	0,75	0,78
а	22,5	0,46	0,51	0,55	0,60	0,64	0,67	0,71	0,74	0,77
а	>25	0,44	0,49	0,54	0,59	0,63	0,67	0,70	0,74	0,77
Р при	_	0,34	0,31	0,29	0,27	0,26	0,25	0,24	0,23	0,22
й«0,8 м
$ при с1=А м	—	0,25	0,24	0,23	0,22	0,21	0,20	0,19	0,18	0,17

Примечание. Для промежуточных значений <р,, Н\й и й коэффициенты определя­ют по интерполяции.

241

Таблица УШ.6

	Расчетные сопротивления /?, тс/м8, глинистых грунтов с показателем
Глубина	консистенции ^., равным
заложения
конца
сваи, м	0	0,1	0,2	0,3	0,4	0,5		0,6
3	85	75	65	50	40	30		25
5	100	85	75	65	50	40		35
7	115	100	85	75	60	50		45
10	135	120	105	95	80	70		60
12	155	140	125	ПО	95	80		70
15	180	165	150	130	ПО	100		80
18	210	190	170	150	130	115		95
20	230	210	190	165	145	125		105
30	330	300	260	230	200
40	450	400	350	300	250	—

нимается по табл. УШ.6. Для фундаментов опор мостов приведен­ные в табл. УШ.6 значения Я повышают на 1,5-уту^в (где Н_в — тол­щина слоя воды от меженного уровня до уровня размыва при рас­четном паводке, м) и умножают на коэффициент т_е=0,6 при по­ристости грунта е=1,1 и на т_в=1,0 при пористости е^0,6 (при промежуточных значениях е коэффициент т_в находят по интерпо­ляции).

Если сваю-оболочку не заполняют бетоном, но сохраняют грун­товое ядро высотой не менее 0,5 м, то при всех грунтах ее прирав­нивают свае толщиной не более 0,8 м и расчетное сопротивление ./? принимают по табл. VIII.1 с учетом коэффициента условия рабо­ты по табл. УШ.З (как для вибропогружения).

Формулы (УШ.8) применимы в тех случаях, когда нижние кон­цы свай или их уширения заглублены в грунт, принятый за осно­вание на глубину не менее диаметра сваи (уширения), но не ме­нее 2 м.

Несущая способность сваи на выдергивание во всех случаях

Ф_в = та 2 И//Л-. (VII. 9а)

где т., и, т/, }₍ и к — те же, что в формуле (УШ.7).

УШ.З. ДИНАМИЧЕСКИЕ И СТАТИЧЕСКИЕ ИСПЫТАНИЯ СВАЙ

Определение несущей способности свай путем динамиче­ских испытаний основано на зависимости между энергией, расходуемой сваебойным снарядом на погружение сваи в грунт, и ее несущей способностью. Метод был разработан в 1917 г. проф. Н. М. Герсевановым для молотов одиночного действия и впослед­ствии распространен на другие виды сваебойных снарядов.

242

При забивке сваи энергия 5 удара молота расходуется на со­противление грунта погружению сваи и на непроизводительные по­тери— нагрев, трение в механизмах, упругие деформации ствола сваи и грунта и пр. Если от одного удара погружение (отказ) сваи равен йф, то

⁵=^Фпр^еФ + ^Эпс*» где Ф_пр — предельное сопротивление сваи;

•Здот — непроизводительные потери энергии.

Отсюда можно определить ^ф_пр. если в процессе забивки заме­рить отказ йф или же по известной из проекта фундамента необхо­димой несущей способности сваи ^ф_Пр найти отказ во и забивать сваю на такую глубину, при которой действительный отказ вф бу­дет равен или меньше вычисленного е₀.

Из решения уравнения относительно ^фп_Р> учитывая потери энергии, получена формула предельной несущей способности сваи по грунту

пРМ

Ф =

пр

\.г пГ е_ф <3п + д ^

пр-

Из этой формулы следует выражение для расчетного отказа ео, при котором обеспечивается требуемая несущая способность сваи ф •

^Эрм 0^__

+ пР\

нри Э_р=(?#.

Здесь Р — площадь ствола сваи брутто, м^г;

п — коэффициент, зависящий от материала сваи, принимаемый рав­ным 150 тс/м² для железобетонных свай с наголовником, 100 тс/м² для деревянных свай и 500 тс/м² для стальных свай с наголовником; Сп — полный вес молота или вибропогружателя, тс;

(2 — вес ударной части молота, тс;

е — коэффициент восстановления удара (при забивке молотами е²=* = 0,2, при вибропогружении е²=0);

^ — вес сваи и наголовника; Эр — энергия одного удара молотов, тс;

Н — расчетная высота падения ударной части (принимаемая по табл. У1И.7), м;

М — коэффициент, равный единице при забивке молотами, а при вибропогружении в зависимости от вида грунта под острием сваи;

Гравий с песчаным заполнением 1,3

Пески средней крупности и крупные средней плотности, супе­ си твердые 1.2

Пески мелкие средней плотности 1.1

» пылеватые средней плотности 1,0

Супеси пластичные, суглинки и глины твердые 0,9

Суглинки и глины полутвердые 0,8

» » » тугопластичные 0.7

При плотных песках значения М повышают на 60%.

243

Для вибропогружателей энер­гия 5_Р определяется по рис. VIII-5 в зависимости от возмущающей силы.

500ВЭр,тс-СН

Отказы е₀ и е$ нужно изме­ рять с точностью до 0,2 мм- Прак­ тически трудно замерить отказ от одного удара с такой точностью. Поэтому при забивке замеряют погружение сваи от нескольких ударов, называемых залогом- При забивке подвесными и паровоз­ душными молотами одиночного действия, а также дизель-молота- Рис. УШ.5. Зависимость энергии Э_р ми без подачи топлива величина вибропогружателей от возмущений залога принимается равной трем ^силы или пяти ударам, при нормальной

работе дизель-молотов—10 уда-_ч рам.

При погружении свай вибропогружателями несущая способность может быть также определена по формуле

ф„р= >(-

153ЛГ_{ВП л} \ — —+ <? ; (VIII. 11)

^0"о6 1

мощность вибропогружателя

#вп= АГ„ч —//,; потребляемая мощность (по показателям счетчика электроэнергии)

При различном напластвовании грунтов значение Я находят по формуле

х =

2М1

2 н

Таблица VI 11.7

Расчетная высота Н для свай

с наклоном не положе 3:1

Тип молота

вертикальных

Я=0,8Я_ф

Я=0,9//_ф

Я=0,4Я_ф Н=Н_ф-Н

Подвесной или паровоздушный одиночно­го действия Дизельный трубчатый

» штанговый Дизельный без подачи топлива

Обозначения: Н. — фактическая высота падения ударной части молота, м; й —

высота отскока ударной части от воздушной подушки (для штанговых дизель-молотов — 0,6 м. для трубчатых /г~0,4 м), м.

244

Таблица УШ.8

	Глинистые грунты с показателем консистенции
	У^>0,75	0,5</^<0,75	0,25<^<0,5
Грунты	Песчаные водонасы-щенные грунты	Песчаные влажные грунты	Песчаные маловлажиые грунты
	Коэффициент X
Пески крупные или су­песь Пески средние Пески мелкие Суглинки Глины	4,5 5,5 6,0 4,0 3,0	3,5 4,0 5,0 3,0 2,2	3,0 2,5 2,0

Здесь % — коэффициент, учитывающий влияние вибропогружения на свойства грунтов, проходимых сваей (для ориентировочных оценок Ф_пр значения % приведены в табл. УИ1.8, точные зна­чения К определяют из сопоставления динамических и стати­ческих испытаний); Л^вп — мощность, расходуемая электродвигателем иа погружение сваи, кВт; А₀ — амплитуда колебаний сваи на последней минуте погружения при скорости погружения 2—10 см/мин (амплитуда колебаний, равная половине полного размаха колебаний, наиболее точно определяется с помощью вибрографов), см; «об— частота вращения дебалансов вибропогружателя, об/мин; (2 — суммарный вес сваи, наголовника и вибропогружателя, тс; Л'п — потребляемая мощность вибропогружателя; Л^ — мощность холостого хода вибропогружателя; т) — коэффициент полезного действия, принимаемый по паспорту вибропогружателя (т) = 0,8ч-0,9); Л_ь П₀ — соответственно начальное и конечное показания счетчика, кВт-ч; I — время установившейся работы вибропогружателя на послед­нем залоге, мин; Хг — коэффициент по табл. У1И.8 для 1-го слоя; /{ — мощность г'-го слоя. Мощность холостого хода приблизительно равна 25% паспортной мощности электродвигателей. Более точно Л^_х измеряют при работе вибропогружателя, подвешенного на крюке крана горизонтально.

Величины, входящие в формулу (VIII.11), определяют на последнем залоге погружения, который принимают равным не менее 5 и не более 10 мин.

Динамические испытания свай широко используют в строитель­стве. Измеряя отказы в процессе погружения свай и сравнивая их с расчетным отказом, устанавливают необходимую глубину и момент прекращения забивки каждой сваи в фундаменте. По пробным сваям, забиваемым до развертывания свайных работ, определяют необходимые длины свай, по которым заказывают их изготовление на заводах. Наконец, динамическим контрольным испытаниям подвергают сваи до устройства плиты фундамента. Учитывая фактор времени, контрольные динамические испытания проводят для свай, забитых в песчаные грунты не ранее 3 сут., а

245

для свай, забитых в глинистые грунты, не ранее 6 сут с момента окончания их забивки. Число свай для контрольных испытаний рег­ламентируется соответствующими нормативными документами на постройку тех или иных сооружений.

Если возникают сомнения в надежности свай, то их подвергают статическим испытаниям. Статическими испытаниями оп­ределяют также несущую способность винтовых, комуфлетных, бу­ровых и прочих свай, к которым динамический метод неприменим. Статический метод состоит в постепенном нагружении сваи и из­мерении соответствующих перемещений. Этим методом находят несущую способность сваи не только на сжатие, но и «а выдерги­вание и на действие горизонтальных сил.

Испытания на сжатие обычно проводят по указаниям соответ­ствующих инструкций (ГОСТ 5686—78), испытания на растяжение и горизонтальные силы — по специальным программам.

При испытании на сжатие (вдавливание в грунт) сваю последо­вательно загружают ступенями нагрузки АР, величина которых со­ставляет 7ю—'/15 предполагаемой несущей способности сваи. Пос­ле каждого загружения ведут наблюдение за осадками сваи, беря через определенные промежутки времени отчеты по измеритель­ным приборам. К загружению следующей ступенью нагрузки при­ступают после затухания осадок; осадки считаются затухшими, ©ели приращение их составляет не более 0,1 мм за 60 мин в песча­ных грунтах и за 120 мин в глинистых, залегающих под нижним концом сваи. При испытании свай для фундаментов мостов загру-жение ведут до тех пор, пока общая осадка достигнет не менее 40 мм.

Рис. УШ.б. Графики статического испытания свай 246

Рост осадок во времени наносят на график (рис. УШ.б, а), по которому строят зависимость окончательных осадок от нагрузки (рис. УШ.б, б). Кривизна графика «осадка-нагрузка» с возраста­нием нагрузки увеличивается и при некотором значении Р осадки резко растут, что указывает на просадку сваи и исчерпания ее не­сущей способности. В этом случае за предельную несущую способ­ность сваи ^ф_пр принимают нагрузку на одну ступень меньшую той, при которой приращение осадки за одну ступень загружения пде-

Рис. УШ.7. Схема установки для статического испытания свай:

/ — анкерная свая; 2 — распределительные балки; 3 — наддомкратная балка; 4 — рельсовый

пакет; 5 — гидравлические домкраты; 6 — поддомкратиая балка; 7 — испытуемая свая

вышает в 5 раз и более приращение осадки, полученное за пред­шествующую ступень загружения. Если же четко выраженной про­садки сваи не наблюдается, то за предельную принимается нагруз­ка на одну ступень меньшая той, которая вызывает осадку, не за­тухающую в течение более суток (при общей ее величине более 40 мм).

Нормативная нагрузка на сваю по результатам статических испытаний может быть также установлена в зависимости от сред­ней предельной осадки фундамента, проектируемого сооружения. Такой прием принят для промышленных, жилых и других зданий. Несущую способность сваи по результатам статических испыта­ний находят по формуле (УШ.З).

При опирании сваи на глины твердой консистенции, плотные крупные и средней крупности пески и крупнообломочные грунты не всегда достигается осадка в 40 мм и более. В таких случаях ис­пытания прекращают, когда нагрузка на сваю достигнет величины не менее 1,5 Ф, где Ф — несущая способность сваи, подсчитанная по формулам (У1П.4)—(У1П.9).

Для испытания сжимающей нагрузкой на испытываемую сваю сверху устанавливают гидравлические домкраты (рис. УП1.7), уси­лия которых передаются анкерным сваям балочным ростверком. Анкерные сваи должны быть удалены от испытуемой на 1,5—2 м, чтобы они не влияли на результаты испытаний. Для замера осадок ставят измерительные приборы (преимущественно прогибомеры), обеспечивающие точность измерения не менее 0,1 мм. Приборы ста­вят в количестве не менее двух, располагая симметрично относи­тельно сваи. Их соединяют с неподвижными реперами, вынесенны­ми за пределы возможных деформаций грунта.

Аналогично проводят испытания свай на растяжение (выдерги­вающую нагрузку) и горизонтальные силы.

247

г)

^й и I^я

с.

Глава1Х. РАСЧЕТ СВАЙНЫХ ФУНДАМЕНТОВ¹

1Х.1. ОСНОВНЫЕ ПОЛОЖЕНИЯ РАСЧЕТА

Свайные фундаменты представляют собой сложные статически неопределимые системы. В зависимости от числа свай и их распо­ложения по отношению к плоскости действия внешних сил можно выделить следующие расчетные схемы: 1) одиночная свая — стер­жень, заделанный в упругую среду — грунт (рис. IX. 1, а); 2) пло­ская поперечная рама, в которой сваи расположены в одном ряду, нормальном к плоскости действия сил (рис. IX. 1, б); 3) плоская продольная рама, в которой сваи расположены в одном ряду, со­впадающим с плоскостью действия сил (рис. 1Х.1, в); 4) простран­ственная рама, в которой сваи расположены в нескольких рядах (рис. IX. 1, г).

В мостовых опорах сваи обычно объединяют мощной плитой или ригелем, жесткость которых можно считать бесконечно боль­шой. Собственные деформации плиты (ригеля) будут при этом от­сутствовать 'И плита (ригель) будет перемещаться, не деформиру­ясь, как абсолютно твердое тело. Для большинства капитальных мостовых опор это предположение соответствует действительности. Таким образом, показанные на рис. IX. 1 схемы будут представлять собой рамы с бесконечно жестким ригелем (плитой) и стойками, погруженными в упругую среду — грунт. Во многих фундаментах в грунт заглубляют и плиту.

В расчетах грунт рассматривается как линейно-деформируемая упругая среда типа Фуса— Винклера с коэффициентом постели, возрастающим с глубиной по линейному закону (рис. 1Х.2). 'Коэф­фициент постели в горизонтальном направлении, нормальном к бо­ковой поверхности сваи или плиты.

С_г=Кг, (IX. 1)

где С_г — коэффициент постели на глубине г (в м) от поверхности грунта, тс/м³; К — коэффициент пропорциональности, тс/м⁴ (табл. 1Х.1).

Для плотных песков К принимают на 30% больше табличного значения. Значения коэффициента К принимают по наименованию грунтов, залегающих в верхней толще Н_к, мощность которой (в м)

й_к=2(й+1), (1Х.2)

где <1 — толщина (диаметр) ствола сваи.

Глубину Н_к отсчитывают от расчетной поверхности грунта при плите, расположенной выше грунта, и от подошвы плиты, если она

¹ В этой главе излагается методика расчета, принятая для проектиро­ вания транспортных сооружений. Подробнее см. К. С. Завриева, Г. С. Шапиро. Расчеты фундаментов мостовых опор глубокого заложения. М., Транспорт, 1970. 215 с.

248

^^1-

1»

>&

^

-X

В) И Г

о

"/'Уф

~^777-

_ъ

*Т

в-в

Рис. IX. 1. Расчетные схемы свайных фундаментов

находится в грунте. За расчетную принимают поверхность грунта после его срезки, а в русле рек — поверхность дна после местного размыва при расчетном паводке. Если в пределах глубины Н_к грунт однороден, то К принимают для этого вида грунта. Если в преде­лах глубины Н_к залегают два слоя разных грунтов, то

(IX. За)

К1&1 (2Й_К — ДО + К₂ (К ~ &1)²

^К=' 1Г

а если три слоя, то

(IX.36)

КхЬ-х [2 (й₃ + й₂) + Н\\ + КФг (2й₃ + Ы + КъЩ

К =

где Ни Н₂, Н₃ — толщины соответственно первого (верхнего), второго и треть­его слоя (Ь1+Ь₂+йз=й_к); Ки Д'г, Кз — значения К для грунтов соответствующего слоя.

737Ш

Формулами (1Х.За) и (1Х.36) учитывают, что на горизонтальные и угловые перемеще­ния сваи основное влияние оказывают упру­гие свойства верхних слоев грунта .

В пределах плиты

К =

(IX. Зв)

2*1

Рис. 1Х.2. Эпюра коэффициента по­стели

249

где К{ — значение коэффициента для 1-го слоя грунта;

Н{ — толщина 1-го слоя грунта в пределах высоты плиты.

Таблица 1Х.1

Коэффициенты пропорциональности К, тс/м*

оооооооооооооооооооооооооооо $2925й2Е"2^{ооосч,г1}*^ц50°⁰^)^''<°⁰°ое\|-*<осооо)-'*<сосоо

для оболочек, столбов и плиты

для свай [(забивных)

Наименование я характеристика грунта

50—200 200—400

400—600

600—1000 1000—1200

65—250 250—500

500—800

800—1300

Текучепластичные глины и суглинки (0,75</1.«51,0)

Мягкопластичные глины и суглинки (0,5</1,=^0,75), пластичные супеси (0</ь<1,0), пылевятые пески (С,6<е< **0,8)

Тугопластичные, полутвердые глины и суглинки (05^1.^0,5), твердые супе­си рь<0), пески мелкие (0,6<е<0,75), пески средней крупности (0,55^е^0,7)

Твердые глины и суглинки (1ь<0), пески крупные (0,55<е<0,7)

Пески гравелистые (0,55^е^0,7), гравий и галька с песчаным заполнени­ем

Примечания. 1. 1_Ь — показатель консистенции; е — коэффициент пористости. 2. Для плотных песков К (для оболочек и столбов) принимается на 30% больше наи­большего значения для заданного вида грунта.

Коэффициент постели под нижним концом сваи в вертикальном направлении

С„_с„=-^-. (1Х.4а)

ч

«о

к

к

«ч I

3

ы I

Щ [

ООООООООООООООООООООООООООО О
СООСМОЮ^-ОСОЬСС'ОО^СОООООЮ-	-юг-с-со-^осоосососо

ЮСМО}^Ю^^10ЮОО^ЮОЪ^О^ЮСОСМ01СОЮОО'-нСО'--<^"^ Г^^^С»0:1СОО^ООО:11^^ЮОЮа}^0^0'*Га^,)'^0 1П--<СОСМ ЮСОСОСОГ^-Г^-ООсОСООСЛОО —«—< —«СМСМС0С0~+<-^т'1ОСО'.О 1^-1^-СО ^ —• ^ —< —< "-" —' —« — -^ —' СМ О! СМ СМ О! СМ СМ СМ СМ СМ СМ СМ СМ СМ СМ СМ СМ

оооооооооооооооооооооооооооо

0(М^ЮОООС^^(ООООС>1^СОСОО(М-^СОК)ОС>)'*СООООСЧ1'*

сосососоооспоспслаооооо-^ *—■—*—*^смсмсмсмсмсососо

сосососососососососо^^^^^^^^^^^^^-^-*^-^^^

ОООООООООООООООООООООООООООО

ЮСМ "^ —с^^^н^.-'10000000000000(000000 СО^ ОМЗ^СО СМ СО '•З' ОО СО О.СП СМ— СОСО^СМСЛ^нОСОСООСМЮСОГ--

СМСО^ЮС7зСМ10 0^СООО-^О^СОСООсС^ЮЮЮЮсЛОСОУ^ОО"^гт^<0^,1 СЪ.-^СОЮГ^ОсМ^Г^О>СМ^Г^ОСОЮОО^^Г^ОСО^--ОСОСООСО Г^сЛСОООСОС^О^СЛО^О^ООО — ^ — ^СМсМСМСОсОсО^^^'ОЮ

ОООООООООООООООООООООООООООО -г⁴ СО ОО О СМ Н-СООООСМ^ЮОООСМ^ОСООСМ^СОСООСМ-^СООО СМ СМ СМ СО СО СО СТ? СО ** "с**■ -"^м "^ -т⁴ «О Ю Ю 1Я >П СО СО О СО СО Г~- (-- Г*» -С-* 1"*«.

сосососососососососососососососососососососососососос^

ОООООООООООООООООООООООООООО

ОСМС0с0С0^СМ'^С0С»Г^С0С0СМ^О<Х>ОС0ЮО^Г^СЙ^С0Г^1ОГ-»

Г^С00^^нс0Ю00^н^Г^^нц^оюО10—'С0^--'0^,1С0^ГС0СМ'—*^-—• ЮЮ^ОО^П^ЮЮООСП^О^-^Ю^-СООС^СОЮГ^СЙ.-* СО Ю 1>-

оооооооооооооооооооооооооооо

00О01^Ю00ОСМТг'С0с0ОСМ^О00О01^С000ОСМ^С000ОсМ 0^г^^^г^сОоОСООО(ЙОСЛа503СОООООО^^-н>-<-1М'>1 СМ01СМ01СМ^СМСМСМСМ0101СМ010101СОСОСОСОСОСОСОСОСОСОС^

ооооооооооо о" о о о" со ©о о ©о"о ©о о о о о

ЮОТОО^СО^©^ЮЮ^ — (ЛЮСО — О^^ОГ^ОЮ^СЛОЭ^СО СМ^ОО^^О^СО^-СО^---СМСОСМООСМСОСМ —'СМ СОСМ О ^ Ю ^

оосооо-^ососмсо-^'—• ооюсм'аъг-иосо — оГоо г-союююююсо"

СС^^ЮСОСОГ^Г^ООСЛСЛО^н^^о^СО-^ЮЮСОГ^СОО'йО ^н СМ СО ^*

где Сося —коэффициент постели в основании сваи, тс/м³;

С — коэффициент постели грунта под подошвой сваи диаметром 5 м, тс/м³; а_осв — диаметр (толщина) сваи, а для свай с уширенной пятой — наиболь- • ший диаметр уширения, м.

Для нескального грунта при глубине Н расположения подошвы сваи, считая от расчетной поверхности грунта, меньшим или рав­ ным 10 м ,„, _лл.

С=Ш, (IX. 46)

а при к > 10 м

(IX. 4в)

С=НК-

Здесь коэффициент пропорциональности К принимают по табл. IX. 1 (как для оболочек, столбов и плиты)-

Для скальных пород значение С принимают в зависимости от прочности породы: при К_Сш=Ю0 тс/м² С=3-10⁴ тс/м³; при #_С5к= = 2500 тс/м² С= 1,5-10⁶ тс/м³; при промежуточных значениях Дсж величину С определяют по линейной интерполяции.

Деформация (изгиб) свай в грунте зависит от упругих свойств

грунта и размеров сваи и характеризуется коэффициентом д е-!

■ ■ 250

с
■еа
*<	> ]
о	14 ]|

а
Ь-;	^ 1
О	^

25"

©©ооооооооооооооооооооо©©©©©

СМ^С000©СМ^ОсЛ©0:1^С0С0©СМ^С0СЮОСМ"^С0с0©СМ-^С0 ^^^^СМ^О^СМО^СОСОСОСОСО^^^^^ьОЮЮЮЮСОСОСОСО СМсМСМСМСМ(^СМСМ01СМСМСМСМ0101СМСМСМСМСМС^С^

ооооосооо ©"о о о о о со ©"© о ©*о оооооооо

(ОгчО^ОООО СОСМСОСОСОСМЮООСОСО-—*СОООСОСОО ^-©СМСОСОСМЮ —* ^10 "^ 1--

смоо^сососмохо^о^^осоо^ослаъ—юсо^аъсосо^-см^-

00С0ОСМ10ОС0СПС0С0СМ— СМСОСОО-^ОСОСО - - - - - - * -

^ «. - - ». - - ► - - - - * - - . ~ * -. -^нЮ01 -^СОСОСОСО

(^^^а^сососо-'^'ьо^юазсосоос^г^ооо'^^* см см со

оооооооооооооооооооооооооооо

СООООСМ^ЮОООСМ^СООООСМ^ЮСЮОО^^ОсоОСМ^СОсО©

ЮЮЮЮСОЮЮ^^^^^СЯСОоОСОООС10)0)050500000^

—* —< —• —«—• —«»-« —« —' ~< -н —' ^^ ^ —• —* —«*-»—* —* -^ см см см^см см см ©о©©©©©© о"о о о <о о о о о о"о оооооо<ооо

С^^ЮС0-^1ОС0С5^С0Г^С1СОС1-< СМ 10 — — СП Ю СМ © СМ —* 1ч- СО ^н С0^С01ОЮОС0а110^СОС0О^001С000ЮО51Г^СМС0ОС0С0О:С0-^' СМ00^^СЮЮС0^ООсЛа000СГ>О0:1^Г^О^О^ОЮС0О0Э00

О^О^О^н^н01СО^Ю10СОГ^С001-нСМСО^ЮГ^СООСМС01Л^-000

_^-,^н^^н_^,—₁^_^,,_ —•смсмсмсмсмсмсмсосососососо-^

00©©©0©0©©0©00©0©©©000©00©00 ©СМ^СООООСМ^СООООСМ^ХзсЛОСМ^ЮсООСМ^ГСООООСМ"^

ооооо^^-^^^смо^смсмо^сососососо^-^^^^ююю о©*о©©оо оо'оо*о"оо оо"оооооо"оооо о о

О^Г^С»0^-^!^ЮСМ^0^С0СМС0С0С0^ОС0ЮС0-^СМ'1^ч--''^'^ГСМ О О —' СОСО —СОСМООСО-^ОС01Г^СО —ОС^ЮО^^МСООО)-«СО О^—-СМ С0-^С0Г-01ОСМ^1^01—-^Г-«ОС0С0О1С01>-СМС0 "^^^^

__,^_^-1^_,^н—. ^н^нСМС>»СМСМСМС0С0С0^^^ЮЮЮСОСО1>*1>-0С>С0

251

ооооооооооооооооооооосооооо

формации а и приведенной глубиной к (безразмер­ной величиной):

*3

о

о о-

^

5],

5 к

^ЮО10С1^СПС?С0С0С0С?00С000Г0С0С0С0^С1^ОЮ'-'^(>| СО СО I*⁴- Г-~ I"--. СО СИ СТ> СТ> ГМ СЗ 1—^ .—( гм гч> гЛ гг> -«+1 -«+1 1Г\ 1/-л гг* г^_ 1^. т г*-1 гтч

•—* СО О 10 О "^ О СО «л ^ и; ь^ со ^ ио ь^ до сэ ои ■"3-'СЛ~г^|СЗ>|-0'—'1^-СЧ ^СО^Г^^СОсЛО^О^СЧО>^^^СЧС^1СОС0^^1С>ОС0^1^-СОСОО^,1

СОСОСОСОСОСОСОСОСО^^^^^^^^^^^^^^-^-^^-^

ооооооооооооооооооооосооооо

С^^ЮСООО^^СООООСЧ^ЮсООС^^ЮОООеч^СОСООСМ"**¹

СО СО СО СО ^- ^-^М^СОСОСОоОСОСПСПТОСЗЗОЮОООО^г^^

000*00000000000000*0000000000

^нОС^сЛСОг^сООС^!^^ООСО<^С^Г^^-ОсОО»ОЮОСООГ^-

ОСО^^СОСЧ^ЙО^^^'СЗСО^^ЮЮСОЮСЗОСЙ'-'^'СООСО СООСО^О^Г^^г^СОСЧСОО^СОГ^^юСЬсОГ^^ЮО-^ООСО^

ю'-о сою ьььсососоас^слоо^^^м^сосо^^^юю

С^СЧ01СЧСЧС^СЧСЧСЧСЧ01^!^СОСОСОСОСОСОСО

ооооооооооооооооооооосооооо

С0001^С0000 01^0000С^^(ООООС\1^СГ)СООСЧ"*^)а;0

оооо"ооооо~оооо оооо оооооооооо"

О-^ОзЮ^СО^-'ССО'^СО-нОСТХЛИСЛСПО —* СО -г)- ^- О) 01 Ю ^ОСМЮСООСОЮсО^^Ь-ОСОЮСО-ч^^^* ^ 1-^ О СО СО О СО ^СОООЮС0050С1СзООО'-'г-(^^₍0']С^(>|СОСОСО'*'*'^1010 ^^^^^^^^^^С0СЧС\|СЧС^(>1^1О1С\|С\|С>1С^С>1С<)С>1С^С>1

ОООООООООООООООООООООСООООО

ЮЮЮС0ЮЮС0МЬ-Ь-^-^^0000С00000О|0)0:0)С1ОООО

ооооооооооооооооооо о© оооо о о

СО^СОСЧ-^000000«1С^СО>0^-С! •-'^СОСЬСОСООЧ'СП^ ^М(^С^01С^СОСССОСОС0^^^^^1010ЮЮСОСОС|Ю^^^

©©©©©©©о©о©о©ооо©ооо©оо©о©о

ооооо^^^^^^с^сос^с^сососососо^^^^^юю

(ОЮЮСОСОСОСОЮСОСОСОЮаЭСОСОСОСОЮСОСОСОСОЮЮЮСЮ

ооооооооооооооооооооосооооо

ОиО^-^-^ОСОЮСОЮСО^н^-СООО*^

^ -.-._-,--.-_,-,--.-.„ .. -сг, со СО -—« СО СО 1-^ О СО I⁴- СО

сососоечооо^соа^^^оосог^^со^ог^соог^юс^аэоо ^осог^о^со^со^ю^ю^сос>1©е\1^10^сп©с>1-^10г-«

Г^0^О«00^10Г--С0О-нС0-^СОГ--ООООСЭОС>г-<₁—*—,^н^-

ОООООООООООООООООООООСООООО

ЮОООСМ^СООООС\1^СООООС\(^СООООО]-^,СОООО<>1'+СОСО

^-^ююююююсососоюг^г^г^г^г^сососососооооосп

СООСОСООСООСООСООООСОСОСООО

1ЛОС0СЮ^Г^С0^С0Г^^нО1С^)ОС0 01С0ЮСС^СГ:С^СЧСЙСЧС0

с^с^с^юсосостэг^союсо^сосо^^о-^со^соосоо-^-'^о^-.

Ю-^СОО! ^-•ООООО^^С^СО'^ЮСОЬ-ОЗ^О^^ОЗС^^ ОООэО ^с>1СО^ЮЮ^ооа>©^е\10Э-'*10С01---а^,)©-не\1С010СО

_й=|/".

-^•1 (IX. 5а)

А=аА, (IX.56)

где Е1 — поперечная жесткость ствола сваи, тс-м²; Ь_р — расчетная ширина сваи, м; й — действительная глубина погружения сваи в грунт, м.

Значения коэффициента а в зависимости от величины подкорен­ного выражения приведены в табл. 1Х.2.

Расчетная ширина сваи вводится для учета взаимного влияния свай в фундаменте, формы и размеров их поперечного сечения:

для свай

*_р= Кф(1,5й + 0,5); для оболочек и столбов

*р=«ф(й+1)к'.

Коэффициент к' находят по формуле

(1—кЛЬг,

*=*'-^,--7^Г^<1- ^(1Х-⁶>

Здесь й — диаметр (толщина) ствола сваи, м;

Кф — коэффициент формы поперечного сечения, принимаемый для пря­моугольных свай равным 1,0, для круглых — 0,9;

к' — коэффициент взаимного влияния свай, расположенных в ряду па­раллельным плоскости действия внешних сил;

к, — коэффициент, зависящий от числа я_р оболочек (столбов) в ряду, параллельном плоскости действия внешних сил, принимаемый при п_р, равном 1; 2; 3 и >4, соответственно—1,0; 0,6; 0,5 и 0,45.

^.р — среднее расстояние в свету (на уровне поверхности грунта) меж­ду оболочками (столбами), расположенными в ряду, м.

Если в разных рядах, параллельных плоскости действия внеш­них сил, расположено разное количество оболочек (столбов), то

с;

_{@- -е- -е- Ь о}

ооооооооооооооооооооосооооо

О О! ОУО> О О О О О ~н ~н ~н -н •-< <М <М О) СМ <М СО РЗ ГЗ ГЗ РЗ Ч< ■«}< т^<

к^

ОООСОСОСООСООООСОСОСОСОСОСО
СПСООООС^н	^СО-^Г-ОЮСГ^ЮЮСООЮ(М	^-СОГ-» СОЮ

_{О ,® ©}

252

сЛ^О>С0С^С0Ю^С010^С0ЮСЧСГ^Ю^ОСЛС0-^С>|О0^,1^С0

СООзОО'-'-'(МСОГО^^,Ю10СО^СОООСзО ^н*01С0^10ЮСОГ^ с^очсосососососососососос^сосососо^^^^^^^^⁴-^"^

Рис. 1Х.З, Схема к определению расстояния 1_р при расположении свай в порядке:

а *■= рядовом; 6 — шахматном

253

к принимают равным меньшему из значений, полученных для раз­ных рядов. При шахматном расположении свай и расстоянии меж­ду осями соседних рядов меньше й+\ м расстояние Ь_р принимают как для фиктивного ряда, полученного совмещением двух соседних рядов (рис. 1Х.З).

Как показывают точные расчеты при Н^2 и опирании свай на сжимаемый грунт, а также при /г^4 и опирании свай на скальную породу или забуривании в нее фундаменты с достаточной точностью можно рассчитывать как рамы с расположенными на некоторой глубине условными закреплениями стоек (свай), не учитывая вза­имодействия стоек с грунтом. Такие сваи можно называть гибкими. При других значениях Ъ непосредственный учет взаимодействия с грунтом необходим.

1Х.2. РАСЧЕТ ФУНДАМЕНТОВ ИЗ ГИБКИХ СВАИ

Расчетная схема. Расчетную схему фундамента принимают в виде многостоечной рамы с бесконечно жестким ригелем (рис. 1Х.4). Для ее расчета примем прямоугольную систему координат 70ХУ. Ось 07 направим вертикально (перпендикулярно .к подошве плиты ростверка), ось ОХ — вдоль продольной оси моста, ось ОУ — пер­пендикулярно к оси моста. За положительные направления осей примем направления, показанные стрелками на рис. 1Х.4. Начало координат может быть расположено в любой точке. Будем считать его в центре тяжести подошвы плиты. Все внешние силы приложим к началу координат. Тогда на свайный фундамент будут действо­вать:

в плоскости 70Х вертикальная сила Ы, горизонтальная сила Н_х и момент М_у;

в плоскости 20У горизонтальная сила Н_у и момент М_х;

в плоскости ХОУ момент М_г.

Будем считать положительными силы, действующие вдоль по­ложительных направлений координатных осей, а моменты, если они направлены по часовой стрелке при взгляде с положительного кон­ца оси, относительно которой действует момент (на рис. 1Х.4 по­казаны положительные силы и моменты). Влияние на работу стоек упругой среды (грунта) при гибких сваях учитываем косвенно пу­тем замены действительной длины их условными расчетными дли­нами.

При действии на сваю продольного усилия расчетная длина сваи Ьы, называемая длиной сжатия, определится по форму­ле (рис. 1Х.5)

ТЕР 1д.= 1₀+ . (IX.7а)

Если свая имеет уширенную пяту, то

ЕР

1.„=Ц + к+ - . (1Х.76)

Здесь Ьо — свободная длина сваи, равная расстоянию от подошвы плиты до поверхности грунта после его размыва, м; Е — модуль упругости материала сваи, тс/м²; Р — площадь поперечного сечения ствола сваи, м²; Ро—расчетная допускаемая нагрузка на сваю (см. п. 1Х.4), тс;

к — глубина погружения сваи в грунт, м; ^₀ _ площадь опирания сваи, определяемая по наибольшему диамет­ру пяты, м²; Сосв — коэффициент постели грунта под пятой (см. п. УШЛ), тс/м.

Полу эмпирические формулы (1Х.7) учитывают влияние на про­дольные деформации свай грунтовой среды (осадок грунта под их нижними торцами).

При действии на верхний конец сваи поперечной силы или мо­мента свая изгибается. В этом случае влияние упругой среды (грунта) может быть с достаточной точностью учтено, если рас­сматривать сваю как заделанную на некоторой глубине. Глубина заделки, определяющая расчетную длину Ьи сваи при ее изгибе, называемую длиной изгиба, находят по формуле

9 94

где а — коэффициент деформации.

Положение каждой 1-й сваи в фундаменте (рис. 1Х.6) опреде­ляется координатами Хг и уг ее верхнего конца, углом наклона сваи к вертикали б_г-_п и углом фг* ее проекций на координатную плоскость ХОУ. Из рис. 1Х.6 следует:

1ёЬ_1х=1ёЪ1„соь_Ч1х;\\ | (IX.9)

«сжатия» и «изги­ба» сваи

где 8{_Х, бгт, — углы между вертикалью и проекцией 1-й сваи на плоскости 2.0Х и 2.0У соответственно.

254

255

Рис. 1Х.6. Геометрические параметры Рис. 1Х.7. Геометрическая схема фун-

1-й сваи дамеыта

Угол бы всегда считаем положительным. Так как наклон свай •практически не превышает 3: 1, то можно принимать соз6гп = 1, Угол фгж условимся отсчитывать от положительного направления оси ОХ в сторону положительного направления оси ОУ.

Расчет свайного фундамента удобно производить методом пере­мещений. За основную систему примем фундамент с условными связями, закрепляющими начало координат (точку О на рис. 1Х.4), За неизвестные примем перемещения начала координат в направ­лении координатных осей и углы поворотов подошвы плиты вокруг этих осей. Тогда расчет будет сведен к кинематически неопредели­мой задаче с шестью неизвестными (по числу возможных в прост­ранстве перемещений).

Во многих случаях достаточную точность дает расчет по пло­ской схеме. Для получения плоских расчетных схем нужно рассмат­ривать отдельно действие внешних сил в плоскостях ЕОХ и ЕОУ (силу N можно отнести к любой из этих плоскостей), а сваи — их длины и наклоны — проектировать на те же координатные плоско­сти. При расчете по плоской схеме задача сводится к трижды ки­нематически неопределимой.

Рассмотрим расчеты только плоских схем '.

Расчет несимметричного фундамента. Рассмотрим расчет фун­дамента (см. рис. 1Х.4) в плоскости 7.0Х (расчет в плоскости 20У аналогичен). В этой плоскости будут действовать силы Ы, Н_х и М_у, приложенные к началу координат, которое совместимо с центром тяжести подошвы плиты. Геометрическую схему (рис. 1Х.7) полу»

¹ Расчеты пространственных схем ,см. К- С. Завриев, Г. С. Шапиро. Расчеты ■фундаментов мостовых опор глубокого залегания. М., Транспорт, 1970. 215 с, а также Свайные фундаменты/Н. М. Глотов, А. А. Луга, К. С. Силин, К. С. Зав­риев. М., Транспорт, 1975. 431 с.

чим, проектируя все сваи на плоскость 10Х. Расчетные длины каж­дой сваи (см. рис. 1Х.5) найдутся по формулам:

С05 В/п

I — 1° •

(1Х.10>

С05 Ъ[_х

Х-ш^^-ш

СОБ Ь[_П С05 В; _г

где /.°дг, /.,%— длина сжатия и изгиба сваи, определенная по формулам, (1Х.7)—(1Х.8).

Угол 6йс наклона проекции сваи к вертикали определим из фор­мул (1Х.9). Для плоской схемы ранее указанное правило отсчета угла фгк приводит к следующему правилу знаков для угла бг»: если свая расположена справа от вертикали, проведенной через ее верхний конец, то угол 8г_Х положителен, если слева, то отрицате­лен. В дальнейшем, для упрощения записи индекс х у угла бг_Ж: опустим.

Согласно методу перемещений закрепим начало координат ус­ловными связями и за неизвестные примем его перемещения: вдоль оси 02— V; вдоль оси ОХ — и; поворот вокруг оси ОУ—р. Пере­мещения V и и примем положительными, если они совпадают с по­ложительным направлением осей 01 и ОХ; перемещение р примем. положительным при повороте плиты по часовой стрелке.

Канонические уравнения будут:

Гг,^ + г_ти + г^Р — N = 0; г_и*ъ + г_ши + /-_црр — Н_х = 0;' . (IX. 11>

^г$г" + V + ^гр{# — ^МУ. = °

где г_тп — реакция т-й связи, вызванная единичным перемещением вдоль и-й связи (например, Гр_ц —реакция закрепления против поворота, вызы­ваемая перемещением и—\, а г„„ — реакция горизонтального закреп­ления, вызванная перемещением V=\ и т. д.).

Величины г представляют собой суммарные силовые факторы (силы и моменты), препятствующие единичным перемещениям плиты. Они слагаются из сопротивления свай и грунта, окружаю­щего плиту. Уравнение (1Х.11) выражает условие равновесия всех сил, приложенных к началу координат, или, что то же самое, отсут­ствие сил в условных связях.

Найдем силы, препятствующие перемещениям плиты. Считая сваю (рис. 1Х.8) жестко заделанной в плиту и грунт, дадим ее верхнему концу единичные перемещения: продольные, нормальные к оси сваи и угловые. Тогда в верхнем конце сваи возникнут уси­лия:

при продольном перемещении — продольная сила

ЕР- рц«——;(IX. 12а)

Л/ Л>

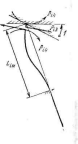
Рис. 1Х.8. Схемы к определению характеристики 1-й сваи

при перемещении, нормальном к оси,— поперечная сила

\2Е1_г

/³

Р2< =

и момент

65/;

рз/

'Ш

при угловом перемещении — поперечная сила

&Е1_г

Рз/ =

*-1М

« момент

4Е/,

-ш

Р4/ =

(IX. 126)

(1Х.12в)

(IX. 12г)

перпендикулярно к оси сваи

51П В;

Дд = V ЯП В/ =

и в свае возникнут усилия, приложенные к верхней отсеченной ча­сти:

ЛГ|— Р1/Д_;у= РисовВ,-; 1

д_/=р_2/д_д=р_2/81п 8,; (IX. 13а)

Щ"= Р3/Д<з = Ра," 51П В,-. ]

При перемещении и=\ (г.' = 0, 6=0) перемещения верхнего кон­ца сваи будут (рис. 1Х.9, в):

Д,, = и 51'п %1 = 81П В,-;

д„ = и сое 8,- = сов В,-

и усилия в свае:

Л^ = Р1/А/у= Р1/⁵'^{П Ь}1>

<?/= Р2/^<э= Р2;С05 0;; (IX. 136)

М/ = Рз/Д(э= Рз/СсвВ,-.

При перемещении 6=1 (<у = 0, ы=0) верхний конец сваи (рис. 1Х.9, г) переместится вдоль оси 02 на величину хф=Хг и повер­нется на угол 6=1. От перемещения вдоль оси 02 в верхнем конце

сваи возникнут усилия:

Л/7 = р_их/ сиз в,;

<?! = Р2<*/ 5111 8,; ■/И,= рз,-^ 51П В/.

От поворота на угол 6=1 усилия будут:

0.1= РЗГ. М{= р₄,-.

Следовательно, при перемещении 6=1 в свае возникнут усилия: ^1 — ?и^х1 ^С05 %[',

С?» = №^х1 ⁸»г В, + рз;; [ (IX. 13в)

/1/= р_зглг/ 81П В/ + Р4;.

а)	Х(
о			X
		01

Здесь /%■ — площадь поперечного сечения М сваи, м²;

/»— момент инерции поперечного сечения 1-й сваи относительно ее центральной оси, перпендикулярной к оси ОХ, м⁴; Ьцг, Ьгм — длина сжатия и длина изгиба 1-й сваи, м.

Величины р называют характеристиками сваи.

Теперь рассмотрим 1-ю сваю с координатой Хг и углом наклона б» (рис. 1Х.9, а) и найдем реактивные усилия в ней, возникающие при единичных перемещениях плиты.

При перемещении и=\ (и=0, 6=0) верхний конец сваи полу­ чает перемещения (рис. 1Х.9, б): \

вдоль оси сваи

Д^ = V С05 8/ = С08 В;;

258

6)
и	у.
	11 ,чл\Ая
	_^"^ \-^\
	*' *ЛЛ
	*?'

Рис. 1Х.9. Схемы действия усилий в 1-й свае при единичных перемещениях плиты

25»

				я=/
				1"
] 1 1	1 '1 / 1	1 1		1 1
"~"Ь-	1 • 1	1		1 с 1 ,

V

₁

		ъ>			\	1 .
					Р*
		Ьг		<		1

,3 = 1

Рис. IX. 10. Схема сопротивления плиты единичным перемещениям

Направление усилий показано на рис. 1Х.9 стрелками, При плите, заглубленной в грунт, сопротивление грунта пере­мещениям учитывается только по торцовым граням плиты (гра­ням, перпендикулярным к оси ОХ). Трения между грунтом и пли­той, а также сопротивление грунта по подошве плиты не учитыва­ют, что идет в небольшой запас прочности. В соответствии с этим, & также в связи с тем, что угол р весьма мал, получим:

1) при перемещении и=1 (а = 0, р —0) сопротивление в каждой точке .плиты равно иг_хК=г_хК (рис. IX. 10), следовательно:

<?= *1 Г Кг_хйг_х + Ь₂ Г К(Н_Х + г₂)йг₂ + - -. = 2 ЬГ^{с);

Й1

(

К

м

= Ь_Х Г Кг_х (Н — г_х) аг_х + Ь₂ \ К{Ь_Х + г₂у(Н₂ — г₂)йг₂ + ... = 2*5<^с);

О й₄

(1Х.14а)

2) при перемещении (5=1 (г> = 0, и~0) сопротивление в каждой точке равно $(к—г_х)Кг_х=(к—г_х)Кг_х, следовательно:

Ну Й1

о

<? = Ь_х | Кг_х (К — г-0 йг-1 + Ь₂ Г /С(й_х +г₂)(й₂ — г₂)йг₂ + ... = 2 *5^(с);

Л,

и.

2*/<

с)

*2

М=Ь§ Кг_х(Н— г_х)гйг_х + Ь₂ Г А^ + г₂)(/г₂ — г₂)2й Юл,

(IX. 146)

Здесь Я"), 5<^с> и /<^с>— площадь, статический момент и момет инерции от­носительно подошвы плиты (оси 07) эпюры коэффи­циента постели каждого участка торцовой грани пли­ты, на котором ее ширина 6=сопб1.

В частном случае, когда ширина плиты постоянна по всей ее

кьт

кьм

12

кьь?

высоте, получим: —..

2^^(с)

2*я^(е) =

2*/^(с) =

Теперь находим реакции г при единичных перемещениях плиты. Для этого следует найти суммы проекций на оси 02. и ОХ сил и моментов относительно оси ОУ, возникающих при единичных пе­ремещениях. Пользуясь формулами (IX. 13) и (IX. 14) и обозначив рог=рн—Р2г, получим (см. рис. 1Х.9 и 1Х.10):

^VV = 2 РО/ ^{С052 В}; + 2 Р2Ь

г_т= 2 рш йпз В| + 2 9я + 2 ЬР^(С);

^гм = 2 к**/ сова в,- + 2 ыА + 22 т*1⁸'^{п ь}1 + 2 т + 2 ^^(с); ^гш= ^гт>= 2 Рог ^с°⁸ ь ⁵'^{т в}<;*

^гъ$ = ^/'рг/= 2 Р0/*/ ^с°5² В» + 2 Р2г*/ + 2 РЗ/ 81П В,-; ''«Р ^{= /}'РЦ⁼ 2 РоЛ ^С05 В/ 51П В,- — 2 РЗ/ ^с05 8^+2 *5^(с).

В этих формулах суммы распространяются на все сваи и на всю торцовую грань плиты фундамента. В большинстве случаев сваи фундамента имеют одинаковые размеры и, следовательно, одинаковые характеристики жесткостей р. Тогда, вынося р за знаки сумм и обозначая через п общее число свай, будем иметь:

г** = Ро 2 сое² В/ + мр₂; I

г_т = Ро 2 зш2 в, + щ₂ + 2 Ь^^с);

(IX. 15)

г_рр = ро 2 А^{со52 в}« + рз 2 А + ²рз2 х, 81п в_{ + пр₄ + 2 *^/(с);

гт = /-ц» = Ро 2 со& В,- Е1п В,-;

^г*$ = ^г№= ро 2 *< ^{С052 в}* + Р² 2 *« + рз 2 ⁵'^{п в}<^;

^г_ир = ^г|а = РО 2 ■*'' ^{С05 8/ 5}'^{П Ь}'¹ ~ ^Рз 2 ^{С05 В}'' + 2 *5^(с)

(IX. 16)

Решая систему уравнений (1Х.11), получим: у= -О-' {Ыа_ш + Н_ха„_н + М_уа„_м); и = Д-1 (Л'а„^ + Нла_иН + ^а_нЖ); р = Д-1 (Л^а_р^ + Я^ря + Л^врд,)

2 .

2 2-

С = /■_ЭТ(/'_иаГрр + ЗГад^р/'^р — Гцц'/'рр — ^гг/^^ги^ ^гр$^гъи

^аьЫ— ^гш^㧧'

^г«р>

а

«

яи>

■ 1"ко.^г-

иЛГ

»Я"

*г>М'

2 ^аиМ ~ ^г»»^грр ''юр'

,2

А,

^; Гт^Ггт Г

рЛ1'

йри

260

261

(IX. 17

*

По известным перемещениям начала координат находят усилия в верхнем конце каждой сваи:

Л^ = рн [(V + рлт/) сов В/ + и 81П В/];1

С/ — Р21 [ — (V + Р-Г;) 8Ш В; + И С08 В/] — р_йР; М/ = РЗ/ [(V + Р-*Т/) 8Ш В/ — и С08 В/] + р4/Р -

Усилия в верхнем отсеченном конце сваи приняты положитель-^ ным'и: для продольной силы Л^, если проекция силы А^ на ось 02-противоположна положительному направлению оси 02; для попе4 речной силы 0,ь если проекция силы 0_х на ось ОХ противоположна" положительному направлению оси ОХ; для момента М{, если мо-* мент М{ действует против часовой стрелки.

Усилия в сваях и давление грунта на торцовую грань плиты фундамента совместно с внешними усилиями должны удовлетво-'| рять уравнениям равновесия, что служит проверкой правильности,, расчета. Эти уравнения будут:

проекция всех сил на ось 02

2 N1 сов 8,- — 2 Я: *»п В/ = И; (IX. 18а) >

проекция всех сил на ось ОХ

2 ЛГ, 8ш 8,- + 2 <?, со8 8,- + и 2 ЬР^ + р 2 65<^с) = Я_ж; (IX. 186) момент всех сил относительно оси О К 2Х-*/ сов В,- — 2 <?/*/ 81П 8,- + 2 М1 + и 2 *5(^с) + р 2 ^^<с) = Му.

(1Х.18в)

Расчет симметричного фундамента и фундамента из вертикаль-, ных свай. Если в симметричной схеме плоскость 20У расположить; в плоскости симметрии, то в единичных реакциях г обратятся в' ноль суммы, содержащие нечетные члены (члены с Хг или зтб,).-

Тогда

О

и система канонических уравнений будет:

гъуУ — Л^= 0; /•««и + ^рР— Н_х=0;

Эта система может быть еще упрощена.

Дадим фундаменту перемещение и=1. Для этого следует (рис. IX. 11) приложить к началу координат горизонтальную силу г_ии и* момент гр„ (момент гр„ обеспечивает горизонтальное перемещение без поворота). Момент г$_и можно заменить силой

1"ии> ПрИЛОЖеН-НОЙ в точке С, на расстоянии

~Г~ (IX. 19)

'ии

С — 262

С т

от точки О. Таким образом, если начало координат перенести в точ­ку С, то в новых координатах ре­акция гр„ обратится в ноль, так как единичное горизонтальное пере­мещение будет вызываться толь­ко одной силой г_ии. Точка С на­зывается упругим центром. Она обладает тем свойством, что лю­бая горизонтальная сила, прохо­дящая через нее, вызывает только поступательное перемещение пли­ты (без поворота).

Перенеся в точку С начало ко­ординат и обозначая все величи­ны в осях 2СХ, получим:

г$_и=г_и? =0;

Рис. 1Х.11. Схема к определению уп­ругого центра

/"/ум — Г и

[— ^г№— /"г/Я ~^рг/— •

Для.вычисления реакции грр нужно составить уравнение момен­тов относительно точки С при повороте плиты на угол р=1. В этом случае на плиту действует момент грр и горизонтальная сила г_мр. Момент этих сил относительно точки С

В новых осях координат канонические уравнения будут:

г_тУ — N=0;

7_иЛ-Н_х^0; I (IX. 20)

ТюТ-м_у=о

при

ЛГ=ЛГ; ~Н_Х=Н_Х; М_у=М_у-~Н_хс,

где V, и, р — перемещения точки С.

Найдя из (IX. 19) неизвестные V, и и р, определим перемещения плиты (точки О):

(IX.21)

у=ь; и=и—$с; р=р.

Подставляя эти значения в (1Х.17), найдем усилия в сваях. При вертикальных сваях зт6*=0 и созб*=1, следова­тельно, единичные реакции будут:

^VV— 2рп".

г_иа=2р2_; + 2*/^?(с);

263

В новых осях координат (с началом в упругом центре) окон­чательно получим

^г»р=^гр»=2^Р1'^ЛГ'^:

^Г«_Р = ^«^ -2 к» + 2*5^(с)-

Чтобы освободиться от побочной 'реакции г_к^=г^, достаточно положить

ЕР-

X: = 0.

^N1

2р1»*/=2-г^_!

Если рассматривать величину ЕР_{/Ьт как некоторую условную площадь сечения 1-й сваи, то левая часть записанного равенства представит собой статический момент условных площадей свай относительно оси ОУ и г_м—г^ будут равны нулю тогда, когда ось ОУ будет проходить через центр тяжести условных площадей свай. Центр тяжести свай находят по общим правилам:

ЕР,

Ь,

2^-*-*п

_г„ _ 'N1

ЕР, '

где Хн — расстояние от г'-й сваи до произвольной оси /—/, параллельной оси ОУ.

Если в фундаменте сваи одинаковые, то

*о=—• (^1Х-²²>

п

Ось /—/ рекомендуется проводить через крайний ряд свай. В симметричных схемах центральная ось свай совпадает с осью симметрии ОУ. Поместив начало координат в центре тяжести свай, получим

/•рр =2 рк-4 + 2 № + 2 Ы^(с), где х_м — расстояние от каждой сваи до центральной оси.

Остальные единичные реакции остаются без изменений. Чтобы обратить в ноль побочную реакцию г_и»—г_еи, следует начало коор­динат поместить в упругом центре.

По формуле (IX. 19) имеем

С= ——. (IX. 26)

2р2/ + 2^^(с)

264

_ N	- их и— ; Г1Ш
Му	Му — сНх

■сг

а?

сг„

Подставляя значения перемещений упругого центра V, И и р в (1Х.21), найдем перемещения точки О плиты, после чего по фор­мулам (IX. 17) получим усилия в сваях.

Если плита не заглублена в грунт, то во всех приведенных выше формулах нужно ее сопротивление положить равным нулю. Для этого необходимо принять Ь = 0. Все расчеты легко программируют­ся для выполнения их на ЭВМ.

Для фундаментов с одинаковыми вертикальными сваями и пли­той, расположенной вне грунта, усилия в сваях и перемещения точ­ки О плиты будут: продольные усилия

Ч

(IX. 24а)

М_У+0,5Н_ХЬ_М

4-

■Щ1

1Ь

п

М,=

N

РЬ

м

2*Й1 +

изгибающие моменты в верхнем сечении

N

(М_У + 0,5Н_ХЬ_М)

1Ь

^Нх¹М

м

(IX. 246)

РЬ

■*ог

и

2и

N

АГ; =

РЬ

м

Е*п/ +

поперечная сила

(1Х.24в)

О, = Н_х: п;

горизонтальное перемещение плиты

_1_ ь

(IX. 25а)

1-м(^Му+ЪМ1_хГ-_м)

1Р

121п

I ₉ ¹¹К \

'N

угол поворота плиты вокруг оси ОУ

(IX. 256)

1 М_у + %,Ж_ХЬ_М

в =—

N

Е р / _ 1Ь

РЬ

м

24 +

^ЬЛГ

265

Определение расчетных усилий в сваях с учетом фактического положения их в пространстве. В результате расчета фундаментов как плоских систем находят продольные и поперечные силы н изгибающие моменты, приложенные в расчет­ных плоскостях 20Х и 2.0У к верхним концам свай. Однако эти усилия не всегда будут расчетными. Так, например, если свая наклонена только в плоско-

10—2644

Рис. 1Х.12. Схемы к определению уси­лий в главных плоскостях сваи

сти 20У, то при расчете в плоскости 20Х эта свая проектируется в вертикаль­ную и усилия в ней будут найдены в вертикальной плоскости, тогда как расчет­ные усилия в свае должны быть расположены в плоскостях, образуемых про­дольной осью сваи и главными осями инерции ее поперечного сечения. Поэтому для проверки прочности свай необходимо усилия, полученные от заданного соче­тания внешних нагрузок в расчетных плоскостях 20Х и 20У, привести к уси­лиям, действующим в плоскостях, проходящих через главные оси каждой сваи.

Рассмотрим общий случай, когда ось сваи расположена наклонно к коорди­натным плоскостям 20Х и 20У (рис. IX.12). Известные из расчета плоских схем перемещения начала координат О обозначим через¹:

и_г — продольное перемещение вдоль оси 02;

и_х — то же, вдоль оси ОХ;

и.у — то же, вдоль оси ОУ;

$_х — то же, вокруг оси ОХ;

Ри — то же, вокруг оси ОУ.

Как и ранее, продольные перемещения считаем положительными, если они направлены вдоль положительного направления соответствующих осей, угловые перемещения положительны при вращении по часовой стрелке при взгляде с по­ложительного конца оси, относительно которой происходит врашение.

Центральные оси сваи с началом координат 0\, расположенные в центре тяжести поперечного сечения головы сваи, обозначим через 0_{Х_{ и О^й про­дольную ось сваи обозначим через 0\2\. Проведем вспомогательные прямоуголь­ные оси: вертикальную ось 0\2\ ось 0\Х', совпадающую с осью О1Ж1, и ось 0\У. Легко видеть, что оси 0₁У₁, 0\2_и 0\2' и 0\У' лежат в одной вертикальной плоскости и что угол между осями 0\2' и 0_Х2_Х, а также угол между осями 0\\" и 0[У| равны углу б наклона сваи и вертикали.

Перемещения верхнего конца сваи в координатах 0\2'Х'У будут:

«V = ^г + х$_у + у$_х; ^иу = ^их ^с°а Чх + и_у сов у_у; и_к,— ы_х 51Н ч_х — и_увтчу\

$х' = $У ^С08 Чх + Ру ^с°5 Чу, Ру = Ру ^81п Чх— Рж зш чу.

Здесь х, у — координаты точки 0\;

4>х, 4>у — углы наклона проекции оси сваи на плоскость ОХУ к осям ОХ и ОУ.

Перемещения верхнего конца сваи в осях 0₁2₁Х₁У₁ будут:

V, = V,, С05 Б + И„, 51П Й; 2_Х х. У

и„ — — V., 81П й + и„, сов й;

т * У

К=К^С05Ь-

Рис. IX. 13. Схема к расчету симмет­ричного фундамента на кручение

Усилия в свае найдутся по формулам:

<?*, = Р2^их, — рзР^;

(IX. 26)

^Мх,= ?$хг— Рз"ь

где р — характеристики жесткости сваи.

Эти усилия действуют на верхнюю отсеченную часть сваи. За положитель­ные приняты усилия, направления которых противоположны положительным направлениям перемещений.

Определение наибольших моментов в свае. По длине сваи изги­бающий момент 'изменяется. В уровне поверхности грунта момент

где М, 0. — момент и поперечная сила в верхнем конце сваи.

Ниже поверхности грунта величина момента зависит от упру* гих свойств грунта, окружающего сваю, и ее жесткости. Прибли­женно наибольшее значение этого момента может быть найдено по формуле

М'=М + <}

(IX.27)

(*+т)-

¹ Здесь подразумеваются перемещения, вызванные одновременным действи­ем внешних сил в обеих плоскостях, при котором определение расчетных усилий в сваях с учетом их фактического положения имеет практическое значение.

Коэффициент т определяют по табл. 1Х.З в зависимости от ве­личины а и На, а при Ла<3 также и от величины

266

10*

267

)

Таблица 1Х.З

от перемещения ф" — крутящий момент в плоскости У^О^Х\

	йа»3,5	Йа=3	Йа=2,5			Йа=2
а			7,=1,5 -Ю-4	^ = 1,5-10—3	^=.1,5-10-2	^ = 1,5-10-4	1;=1,5-10_3	15 = 1,5-10—2
			Коэффициент т
0,10 0,125 0,15 0,175 0,20	0,75 0,75 0,75 0,75 0,75	0,7 0,7 0,7 0,7 0,7	0,67 0,66 0,65 0,65 0,65	0,70 0,68 0,66 0,66 0,66	0,81 0,77 0,75 0,73 0,71	0,55 0,54 0,52 0,52 0,51	0,65 0,61 0,57 0,56 0,55	0,94 0,88 0,81 0,78 0,75 /

сваи повернется на угол ф и переместится нормально к радиусу р/

На величину Ы;=фр;.

Разложим перемещения головы сваи на перемещения в двух плоскостях, каждая из которых проходит через ось сваи 0\2.\ и одну из главных осей инер­ции ее поперечного сечения 0\Х\ или 0\У\. Перемещение ф разложим на пере­мещение в плоскости 2\0\Х\

ф' = ф 81П В/

и на перемещение в плоскости У\0\Х\

ф" = ф сов в,-.

Перемещение щ разложим на перемещение в плоскости 2₁0₁К₁:

и'=фр,-С05 (?/ + (!,■)

и на перемещение в плоскости 2.\0\Х\.

и"= фр_г 51П (?/ + сс/).

Здесь б,—угол наклона оси сваи к вертикали в плоскости 2\0{У\\

аг — угол между положительным направлением оси ОХ и радиу­сом р,; ф_г—угол между проекцией на плоскость ХОУ положительного на­правления оси сваи 0\2\ и положительным направлением оси ОУ. В результате этих перемещений в свае возникнут следующие усилия, препят­ствующие кручению (повороту плиты):

от перемещения ф' — изгибающий момент и поперечная сила в плоскости 2,0,*,:

4ЕЛ,

М_ф,=

■ ф 81П 8/ ,

'М

6ЕГ_и

<?*.=

Несимметричные фундаменты нужно рассчитывать как пространственные.

268

М_ф„ = — -— ф сое Ьг,

от перемещения и' — продольная и поперечная силы в плоскости 2.\0{У\\

ЕР

ЛГ_И» = —— ф_Р/ С05 (10/ + И/) 81П Й/, С„, = "э—*" фр, С05 (?/ + О/) 81П ЬГ,

от перемещения и" — изгибающий момент н поперечная сила в плоскости 2,0 А:

^6ШУг

^миг = — —7Т~ 4Ф/ вш (<(1 + а,); ^см

^12Е1У1 <?«•= — ~7з— 4*Р» (51П <а + а,-).

Здесь 1_У , — момент инерции поперечного сечения г-й сваи относительно оси О^й 1'_х — то же, относительно оси 0\Х\\

/о ■— полярный момент инерции поперечного сечения г-й сваи; О — модуль сдвига материала сваи (для железобетона О=0,4Е). Остальные обозначения прежние.

За положительные усилия в сваях приняты: продольная сила — сжимающая; изгибающий момент и поперечная сила, если они вращают отсеченную часть сваи по часовой стрелке при взгляде на- сваю с положительного конца главной оси инерции поперечного сечения сваи, перпендикулярной к плоскости действия изгибающего момента и поперечной силы; крутящий момент — при кручении отсеченной части сваи по часовой стрелке при взгляде с положительного на­правления оси 0\2.\.

Беря проекции усилий в сваях на плоскость ХОУ и составляя уравнение равновесия, выражающее равенство нулю суммы моментов всех сил относи» тельно точки О, получим

2 Г — Щ' + ^Ми") ⁸>^{п 6}«- + ^Мг ^{С08 В}<"^{— (<?}4" + Сф") Р/ + + {И_ит 5Ш В/ — С_цг сое В,-) _Р;] = М_г,

где плечи:

Р; = р/ 81й (у/ + а,-);

Р;= р,-со5(9,-+ а,-).

Знак 2 означает суммирование по всем сваям.

Обозначая через М значение выражения в квадратных скобках при ф=1, можно записать

Ф2м=м_г,

откуда ф — М_г : 2 ЛЬ

Определив таким образом угол поворота плиты фундамента, по приведенным выше формулам можно найти усилия в сваях.

269

(IX. 29)

Рис. 1Х.15. Деформация основания столба

1Х.З. РАСЧЕТ ФУНДАМЕНТОВ ИЗ СВАИ КОНЕЧНОЙ ЖЕСТКОСТИ

Расчет столба конечной жесткости. По излагаемой методике рассчитывают фундаменты, учитывая совместные деформации свай и окружающего их грунта. Такой более точный расчет необ­ходим, если величина Н—аН<2 м при опирании свай на сжимае­мый грунт и й<4 м при опирании на несжимаемый грунт. Расчет­ные схемы таких фундаментов показаны на рис. IX. 1. Основным, их элементом служит столб, заделанный в упругую среду — грунт,' деформации которого необходимо изучить в первую очередь.

Рассмотрим столб шириной Ь_р, нагруженный в уровне поверх­ности грунта горизонтальной силой #о и моментом М₀. Оси коор­динат расположим, как показано на рис. IX. 14. Дифференциальное уравнение изогнутой оси столба при коэффициенте постели, пропор­циональном глубине, будет

Е1 —^- + КЬ_ргу=0.

(IX. 28)

йг*

м₀

а,2Е1

н_л

С,+

•О,

а»Е1

Решением этого уравнения является функция

Здесь

Е1 — жесткость столба на изгиб;

Уо,

К — коэффициент пропорциональности (см. п. VIII.1); Фо-—прогиб и угол поворота сечения столба при 2=0; а — коэффициент деформации см. формулу (1Х.5а), численные зна­чения которого приведены в табл. 1Х.2; Ль В^С^х — функции влияния безразмерного аргумента г=аг.

М₀

■У/ЛШЖ "7ЯШ.

в.) Но

\г

Рис. IX. 14. Расчетная схема одиноч­ного столба

Функции влияния выражаются следующими сходящимися ря­дами с бесконечным числом членов:

_г5 _г 10 _г15 2%0

А_г= 1 —-—-+6 - — 6 - 11 +6 ■ 11 ■ 16' — ...

5! 101 15! 20!

- 7б ¹7и ^16 721

В_х=г — 2 + 2-7 —2-7- 12 +2-7-12- 17 - — ,

6! 11! . 16! 21!

г2 7? ^12 717 722

^С1==-2Г-³^Г ^{+ 3}-⁸127-³-⁸-¹³1?Г ^{+ 3}-⁸-¹³-¹⁸127- Т³ 7⁸7¹³71⁸7²³

/?!=—— —4—- + 4-9 —4-9 -14 Ь 4 ■ 9 • 14 • 19

3! 81 13! 18! 23!

Последовательно дифференцируя функцию (1Х.29), получим:

-**- = _тА% ^^в₂₊^._С2 + ~^_ГП₂; (1Х.30а)

а а а²Е1 а³Е1

М._Х Юп Мг, Н()

-^Т=-тАз + —Яз + -г^г С₃ + —%- Оз; (1Х-306)

-§- = УоА_{4 +} ?°-_{Щ +} ^. _Л^_ (1Х.80В)

а³Е1 а а^Е/ а³Е1

где А₂ ..., В₂ ..., С₂ ..., В₂ ..., И^ — функции влияния, полученные соот­ ветствующим дифференцированием функций А\, В_и С_г и !>!.

Значения функций влияния и их производных для аргумента от € до 5 приведены в табл. 1Х.4.

В выражениях (1Х.29) и (1Х.30) положительными приняты: прогиб у_г в положительном направлении оси ОУ; угол поворота ф₂ при повороте сечения против часовой стрелки (на рис. IX. 14 угол ■фо отрицателен); момент М₂ при растяжении левых волокон столба (при кривизне выпуклостью в сторону отрицательной оси ОУ); по­перечная сила 0__г при действии на верхнюю отсеченную часть в на­правлении отрицательной оси ОУ.

Полученное решение в строительной механике называют реше­нием в форме метода начальных параметров; за последние приня­ты прогиб уо, угол поворота фо, изгибающий момент М₀ и попереч-яая сила О_₀. Неизвестные начальные параметры у₀ и ф₀ определя­ют из условий опирания нижнего конца столба. Рассмотрим два случая опирания.

Первый случай: подошва столба расположена в нескаль-ном грунте или опирается на скалу без заделки в нее (рис. IX. 15). Под действием внешних сил М₀ и Я₀ подошва повернется на неко­торый угол ф;г. На элементарную площадь ёР_осш подошвы (основа­ния) столба будет действовать реактивное давление

<1Ыу= Учь.С_оснаР_осп.

270

271

Это давление создает элементарный момент относительно оси, проходящей через центр тяжести подошвы перпендикулярно к пло­скости У 02:

ам = у.аы_у = — ^лСосн^осв ■

Момент Мн от отпора грунта по подошве столба получим сум-* мированием элементарных моментов, распространенных на всю площадь подошвы:

М_к = Г Ш = -теСдаЛда,. (1Х.31а1

оси

Здесь Сосн — коэффициент постели грунта в вертикальном направлении на! глубине к [см. формулу (1Х.4, а)]; /осн — момент инерции площади подошвы столба.

Знак минус в выражении (1Х.31а) связан с тем, что положитель­ный момент М_н от отпора грунта по подошве столба возникает при отрицательном угле фл ее поворота.

Выражение (1Х.31а) является одним из условий для определе­ния начальных параметров. Вторым условием будет

С)_й=0 (ГХ.316)

(силой трения по подошве столба пренебрегаем).

Второй случай: нижний конец столба заделан в скальный грунт. В этом случае начальные параметры находятся из условий:

№г=0; (1Х.32а>

9й=0. (1Х.32б>

При заделке столба в скальную породу глубину его заложения принимают

Л = Л_с + да,

где Не — глубина расположения поверхности скальной породы;

АЛ — дополнительная глубина, равная 0,51) при забуривании в слабые раку­шечники или мергель, П/3 при забуривании в известняк или песчаник и равная нулю при забуривании в кристаллические породы {В — диа­метр столба).

Чайдем единичные перемещения столба в уровне поверхности-грунта, вызванные действием силы Н₀=1 (М_о=0).

При опирании столба на нескальный грунт или скалу (без за-буривания в нее) используем выражения (1Х.31а) и (1Х.30а), иа которых следует:

а—<

м

я к ч

5

ооо|'*оо(м^^'-10010-<'*ьмю^1ЬМ01!м-<'*1Со^со1М'-|

ооооооооооооооо.

I .ч СО

I I I

ооооео^г-1н-101га(м(0 0юоюпм»^0(оюмо|^ооо

ООООСПСПС35СПООГ~.1ЛС<1Г~.СЛООСч10 05 00-*-*—1СМ-*п->00«300!МС35

юоп

ОООООС)ФС10101СТС:00|^С010г003100СОРО'-'СО^СОдаООЮ

О —<<М

г-чмт

ООООООООООО'

I I

ОООСОССОООО-^ЮСОЬЮ^ЫОЮСОЮ^- ^(^СОС^СООСОООО ОООО00^ЬС^«0^Р5'-^,10'-^,'^^Ю^^^,С0ЮС\)^.О00'-1О'--1а1(Г1 ОООСПС!аоОЬ^ОСОСООООООС010^УЭСТ10-^(>)СО^'*ООСОгн^.

I I

_ __, г^о о о оо^осГоооооооооооо"оо ^(N«9^^^

I I

_{°°11"??????????????????тттт??т::"}

О^СО^СОООО^СО^ЮсОЮООСОО>^а>ОСОО^СОСГ>СОСОСОООО'—' 00^^00<^Ь^^СО'-н^-^|Л'ОСПСО'-<гнсОС0010СОЬсОО)К1000 ОСОО-^С^ССЮС»С^ЮС^00С010Ю^'-<С0С^О(>)01С^СС10Ь'--|1ЛЮ ООООООООО-нгн(»МИ^ЮЮ00агнГ0Ь^ЬО)СС05 10с^^

осГо осГо о"о о о сГсГсГо о о о о о ннн^меом -^-^сТ.—«

ООООООС0Ю0йМгн^^.[ч.С0^С0^1>1ОС^ЬС^ОС0'Н^^.(0О ООООООаОООК-^СОООСМЬСООСОСОСЙО'-ЮОЬ'^ЬО^^Об 01ПЮ001ПО>^0>^а>СО^^СОСО^ОСО^^С^СОСО<»^СОСОС^^

о о о о о о сГсГо о о сГсГсГо 1—1 *~* *~1 »-• —"—«с^(мс^сосос^ооос^

I 1 ^

о"оО 0"0 0 0^Ч0*'ООС _^_7_Г_,„₁_н_₁^^_ч_^_н__юсОе^

М_Н= -С

\ а а³Е1 /

осн' осн

Подставляя это выражение в выражение (1Х.306), получаем:

аЕ1 \ а а³Е1 ) а а³Е1

(1Х.ЗЗа> 272

I*

000(Х)^^ЮОЬОО^СО^СС¹СО'-<0'-1СОЬ'С^'-|'--'^,*000101СОССО

оооаспNсо^^сNоююс^осNсосоо^-I(^ос^)а)^-^|•^^ноо)соср^-^

0 000501.0501СЛ<ЛС)01С75а05СТ)0)0)ОООС)^ЬЮГООС0 0101000СО

1ММ7

■* С^ СО -^ Ю СО (^ 00 СП С^-^СООО Ю Ю

оооооооооо*

273

I (М

ТС

о

«

о о,

с

274

Э2Я?2?^сп52Ь:^^сп0юиз'^-^'^-''^-^°огоо«з—I—1—1^спцзо10«о

ОС^СПСПСПСПСП05СЛСПСПСП0500001^.СОЮгО'-нОСОЮоО-^^,10001—I»—«СО

^н^^ОООООООООООООООООООО--нСч1^СОГО го" СП 1--

•-■СМ О! С^|

ОО^ОСЯСХЭС^ОС^СПСГ>0000Г0С0Сч1С0^О1-~.Сч1ЮСч1^ОС^^>0СП10

922°9^0,н^^1Лсй^оо1Л101^пэ-нсос310со^^1005^,*01^05ь

ОООООООООО.-гн^'0^(0с0ОсЧС0(3)С001С0Оа!ЦЗШОО

юсо О I 1 со

ооооооооооооооооо_Т7Т7с_|1._ПТ2

ОС0ЬОС0^-<ЛС0О^ССС^ОО'^С1С^С0Ь1000С^'-1С0аО10С^ОО ОСОСООСОСОСПОЗСОООСТэС^ЮЮЮО^^^^а^Ю^С^О^СОСЪСОе^⁴* ООСМО^^(^^ОСМС^СМ^ООСООСО^^(^ОСООС^^С©^^>Л

оооосм^^^(^^со^^^о^ю.^осм(^юсм^^сос©1осло

ооооооо'Н^-(мсо^ю^аI^нсос^О)(мюсо(N^-^о^^РЗ(X)^.

ОООООООООООООООгнн^н(»(мг0^1ЙЦЗЮ100С>М

IIIIIIIIIIIIIIIIIIIIII I I I I |~^ю

ООООО<Й-^О10С0'-1С0С0С^,0С000С0Г0000100'-|'--|>00000с0С30ОС ОООООа0101(ч^сОсОЬ.Ю'^Ю0 1>1С^а1'НСООСПЮ(>10СО'Нг-|

оо^^со^г^^^осъо^сосоо^сг1^сп^г>1сосо^со(^^ссоо

ОООСО^^нС^^СО^^<^1NСОа^-^(^1С^,ОЮ^^Ой'-ГОтI^чСОСпОСNСNО

ч СП Ю СЛ

>Сч1СМ(М!М ■

I I I I

ооооооооооооооо-

I I

оооооэ--н^10"*1оюсос^о^С1ю^(мст1сооо-а1спсомооо

о о о о аз а> сп сп ооь то со со оо о ю со -н а> юю с4ю ь "-н ■* >л "* ю ооооаас^спспо^аспсоьЮсоосогнсо^Ь'о^спглю^.оою о^^сNсссс^юсо^^соспо^^смсо^юю^соо^осссп^^ооооо^сс

«ОО ОЮЮОО ■—< | 1^СМ^

ооооооооооо.

ооспсп^смососссNс^^^оо^ч1^^^о^осос^о^^оосссоспсо^с^сс•--^

ООС)СПСПСЛОСТСПсЮК»0С0ОЮ^С^-^(>100ОЬ^,*ЬОС0'*₁-|00О

оослослс^!слослооооососо(^союсо^смос©^;ос^

1—|^^ОООООООООООООС;ООООООО'-нС0^ч*О(^.^СЛ

1111 177ЧТ

о^со^со^о^^соос^оосоос©^ю^^г^сп(^оосп(^.оооо

ОО-^С0-^С^<»О'^С0С^С^СГ>«О<таС0^^--10СС'С0СМ00^1^С01^.1С|Ю

оооос^юоо^т^со^пьспосо^ьсосо»л!соа1^.а1сооа1со оооооо^с^союсо^^.со^1^1^спI^I^.^-'Ососп-^сп'*соо■5^,

ООООООООООО ^^С^С0-^ЮС000ОСССПС01О(^-СП10(^-СС|СЛ сГсГо О О о" о" о" о" о" о" о" О О О О о"о О 1—< -нгнс^СО т*Чо СП ^н (^. 1—I

I I I I I I I I I I I I I I I I Н I I I I М МТ I^м

ОЬС0О^С0ОС0С^^С^С^^СС10ООСС^С0Ю'*ЬС0'-<Х--<С0С0О

ОО^^ООСО^Ю^СО^^^ЮСОСОсОЮ^ЮСО^^СООСТЭ^ОэСО ОООО^С^СОЮООС^^МХЮЮЮ^.ОЮ'-нОСП^МО'^гНгнСОЬ-ООООООООО^-н(>1С^,<1С0^^,0С000СП--нс^С0^С0'-|ЮСПС0С0СЛ

ооооооооооооооооооо_{7ТтТ1)Т7Т}

г—' СЧ СО тС Ю СО Г-- ОО 05 -<МЮ'*ЮЮ|^аоа) СМ^СООО Ю Ю ОООООООООО^гнгчгнгн_гч1-чгЧгчгн(^(МИ(^(МПК)'**>Л

Из выражений (1Х.30в) и (1Х.316) следует, что

*ьА* + ^ЖВ_а + -±—О_а=Ъ. (1Х.336)

а а³Е/

Совместным решением уравнений (1Х.ЗЗа) и (1Х.336) нахо­дим единичные перемещения столба в уровне поверхности грунта:

₍₀) ₌ ^_ . (В,Р₄-В₄Р_{г) +} К_кф,Р<-В₄Р₂) ^нн ФЕ1 {Аф₄—А₄В₃) + Кн{А₂В₄ — А₄В₂) _В(0) ₌ I (^3^4 - А₄Р₃) + Кн (А₂Р₄- А_АР₂) _{(1Х 34б)}

^мн &Е1 " (А₃В₄-А₄В₃) + Кн(А₂В₄ — А₄В₂)

_Яр„/С_Л=-%^.^. (1Х.34в)

аЕ I

Если на столб действует только момент Мо=1 (#о=0), анало­гично можно получить (Ъмм⁼ —*о)

₍0) ₌ 1(АзС₄ - А₄С₃) + Кн (А₂С₄ - А₄С₂)

^мм аЕГ ' (А₃В₄~А₄В₃) + Кн(А₂В₄~А₄В₂) '

Перемещение ^в//л= ^вУя определяем по формуле (1Х.346).

Величина Кн определяет влияние сопротивления грунта пово­роту подошвы столба на его перемещения в уровне поверхности грунта. Анализ показал, что, когда при опирании фундамента на нескальный грунт Н = аН^З, а при опирании на скалу й=аЛ^З,5, без ущерба для точности расчета можно принимать /(л=0.

Если столб заделан в скальную породу, то, учитывая условия (1Х.32а) и (1Х.326), аналогично будем иметь:

₅(С)__^. Ы-В& ^нн аЗЕ1 А₂В₁ — А₁В₂

_Б(0) _ .(0) 1_ . _Д.2С1-В1С₂.. _(1Х д_6б)

_В(0) -Л-. А&1-А& _{т (1Х}.збв)

^мм аЕ/ А₂В₁~Аф₂ ^К '

В выражениях б⁽⁰> значения функций влияния А, В, С и О с со­ответствующими индексами берутся для аргумента х = аН.

Численные значения выражений, входящих в формулы для оп­ределения 6<°), приведены в табл. 1Х.5.

Зная перемещения столба на уровне поверхности грунта от еди­ничных усилий, можно определить перемещения на том же уровне от силы Н₀ и момента М₀:

_т = Н₀ъ%>„ + М₀Ь%; % = - ("<А + Л*сО-(^1Х -³⁷>

С помощью выражений (1Х.306) и (1Х.30в) строят эпюры изги­бающих моментов и поперечных сил в сечениях столба.

Горизонтальные'давления на грунт по боковой поверхности столба

с_{г= КяВя}= Кг (щАг + ^ В, + -^- С, + -^ ^). (1Х.38)

275

^

I Расчет фундамента из несколь­ких столбов конечной жесткости.

Рассмотрим симметричный фун­дамент, состоящий из нескольких вертикальных столбов, объеди­ненных сверху распределительной плитой бесконечно большой жест­кости (рис. IX. 16). Действующие на фундамент внешние силы при­водим к точке О — центру тяже­сти подошвы плиты (рисунок со­ответствует расчету в плоскости 20Х). Выражения перемещений столба (со свободной головой) на уровне низа плиты от единичных усилий, приложенных к тому же уровню, имеют следующий вид.

1. При действии горизонталь­ной силы Н_х= 1;

горизонтальное перемещение

Т^чТч^

'•I

Рис. 1Х.16. Расчетная продольной рамы

о?>\\УУ^ -ХЖ

схема плоской

^ьяя =

ЗЕ1

Ь% + Ь1Ь^_М+2ЦЬ%;

угловое перемещение

/²

°мн~-

°НМ'

2Е1

2. При действии момента М_у=1:

- + Мйи + »да

°МН'

горизонтальное перемещение угловое перемещение

^ьмм

_ _^°_ _В(0)

ми-

Е1

= О ЯЛ,

Вертикальное перемещение головы столба, вызванное силой N=1, будет складываться из деформаций тела столба и основания. Пренебрегая силами трения по боковой поверхности столба, это перемещение

°рр =

ь₀ + ь

ЕЕ

С₀ск' оси

при

где ЕР — жесткость столба на сжатие;

_Кп _ коэффициент, учитывающий уменьшение деформации основания с уменьшением площади подошвы столба; йосн — диаметр подошвы столба, м.

При единичном горизонтальном перемещении плиты в голове столба возникнут горизонтальная сила рнн и момент рмн\ эти силы

277

''

найдем из системы уравнений (угловое перемещение равно нулю):

?нн^ьнн + Рлш⁸лш= !; Рни^ьмн + Рлш^влш = °-Отсюда

"ММ

Р//я = -I—: ^—; (1х.зэк)

^ьнн^ьмм ~ ^ъмн

~^ъмн Ын = ~_ь : Г2 • (1Х.396)

Усилия р_Мм и рнм в голове столба от единичного углового пе­ремещения плиты получим дз уравнений:

Рмм^ъмм + Р/ш⁸л//= ¹"> Рмм^ьим + Рнм^ьнн= °> Откуда

рлл1= т—: п—; (гх,40а)

^ьнн^ъмм — ^ънм ~^ьнм

Как и следовало ожидать, бмн = бнм.

Сила дрр от единичного вертикального перемещения

РРР=~Г~⁼ / Л-Н и • ^(1Х-⁴¹⁾

Ьрр ь₀ + я ^ к_п

Е* ^осн* осн

Усилия р нужно вычислить для всех столбов. Суммарные еди­ничные реакции метода перемещений, возникающие при вертикаль­ном V=^ и горизонтальном ы=1 перемещениях точки О плиты, а также при повороте р=1 плиты относительно той же точки, бу­дут:

г^= 2 р_рр; /•««= 2 9_НН'< | ₄₂

^/"рр = 2рл1л + 2^л:2рря; ^/"_иР = '"р«=2Рл1я. I

Неизвестные перемещения плиты V, и и р определяются кано­ническими уравнениями (1Х.11) метода перемещений, решив кото­рые, получим:

N г^Нх — г^Му

-—; и= 1 ;

(1Х.43)

ГидМу — Г_и?Н_х

^Р~ Г г —г¹

' ии' р р ' _ир

278

)

Изложенный способ расчета фундаментов из нескольких стол­бов отличается от расчета высо­ких свайных ростверков тем, что 9 нем распределенное сопротив­ление грунта не заменяется ус­ловными жесткими закреплени­ями.

"—4 1

0,15 0,1 0,25 0,3 0,35 0,4 0,45 0,5 0,55 Й

Рис. IX. 17. График для определения глубины им расположения условной заделки столбов

Канд. техн. наук К. С. Заври-евым проведен анализ возможно­сти использования условных жест­ких закреплений при расчете фун­даментов из столбов. Анализ по­казал, что при глубине заложения столбов, отвечающей условию й=аЛ<2, перемещения фунда­мента (V, и, и р), а также усилия

Л', Н и М, действующие на голову каждого из столбов, можно оп­ределять по формулам гибких свай (см. п. 1Х.2), если расчетные длины столбов на изгиб .^м и сжатие Ьц определять по формулам:

_К„ЕР (IX. 44)

^ОСН' ОСН 9 )

где Н_м — глубина (от поверхности грунта) расположения условного жесткого закрепления против горизонтальных смещений и поворотов столба, оп­ределяемая по графику (рис. IX. 17) в зависимости от коэффициента

Использование расчетных длин, вычисляемых по формуле (1Х.44), обеспечивает достаточно хорошее совпадение результатов расчета, основанного на использовании условных жестких закреп­лений, с соответствующими результатами расчета, учитывающего распределенное сопротивление грунта перемещениям столбов. Исключение составляет определение величины наибольшего момен­та М_н, действующего на части столба, заделанной в грунте. Эту величину М_н К. С. Завриев рекомендует определять по формуле

М

(IX. 45)

н-

М + <3(Ь₀ + /1_ММ),

где Ад

-глубина, определяемая по табл. 1Х.6 в зависимости от а и 2=00/1, а при г=аН<3 также и от значения коэффициента т)=Л/₀сн: (Е1), учитывающего влияние сопротивления грунта повороту подошвы столба на величину Мн-Формула (1Х.45) основана на схеме, в которой столб на глуби­не Н_Мм рассматривается заделанным, а выше этой глубины сво­бодным от грунта.

Способ, основанный на использовании условных жестких за­креплений, не охватывает случаев расчета фундаментов со столба­ми, погруженными через толщу нескальных грунтов и забуренны­ми в скальную породу.

279

Таблица IX.6

	г>3,5	г=3		2=2,6			г=2,0	1
								г, = 1,5-Ю-^
а			т)-1,5-10—4	1) = 1,5-г0~3	г;=1,5-1(Г~2	1] = 1,5.НГ^	г,=1,5-10—а
				Глуб	нна кмм,	м
0,1	7,3	. 6,9	6,5	6,8	7,8	5,3	6,3	1- 9,0
0,125	5,9	5,7	5,4	5,6	6,4	4.4	5,1	7,2
0,15	5	4.6	4.3	4,4	5,0	3,5	3,8	5,4
0,175	4,3	4,0	3,7	3,8	4,2	3,0	3,2	4,5
0,2	3,7	3,5	3,2	3,3	3,5	2,6	2,7	3,7
0,225	3,3	3,1	2,9	2,9	3,2		.
0,25	3	2,8	2,6	2,6	2,8	.	.
0.275	2,7	2,5				.
0,3	2,5.	2.3
0,325	2,3		—			.
0,35	2.1	—				,
0.4	1,8	—	—	—	—	—	—	—

Плиту можно считать абсолютно жесткой, если ее толщина Н_п составляет не менее одной четверти расстояния Ь_кр между осями крайних столбов, расположенных в расчетной плоскости.

Если расчет ведется только на горизонтальную силу Н_х (при М_у = 0), плиту принимают абсолютно жесткой при условии

Т--7Г^<2,0'

где /_п — момент инерции поперечного сечения плиты относительно оси, нор­мальной к плоскости действия сил; Ь — расстояние между столбами в расчетной плоскости; Ьм — расчетная длина столба на изгиб;

/с — суммарный момент инерции столбов, расположенных в одном ряду, нормальном плоскости действия сил.

Если плиту ростверка нельзя считать абсолютно жесткой, то фундамент рассчитывают как раму с упругой заделкой стоек на уровне поверхности грунта. Упругая заделка стоек характеризует­ся единичными перемещениями б<°>, которые определяют по фор­мулам (1Х.34) — (1Х.36). Раму рассчитывают по общим правилам строительной механики, причем жесткость плиты (ригеля рамы) учитывают только на участках между столбами в свету.