
Математика. Экзаменационный документ
.doc
МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ (МАДИ)
УТВЕРЖДЕНА
на заседании кафедры высшей
математики (протокол № от декабря 2014 года)
Зав. кафедрой высшей математики
проф. Буслаев А.П.
ПРОГРАММА ПИСЬМЕННОГО ЗАЧЕТА ПО
УЧЕБНОЙ ДИСЦИПЛИНЕ
МАТЕМАТИКА
Факультет: ДП
Подготовительные курсы
Форма обучения: очная
Курс 1, семестр 1
Москва 2014 г.
На выполнение письменной зачетной работы по математике отводится 120 минут (2 астрономических часа). Билет состоит из двух теоретических вопросов и двух задач. Задания можно выполнять в любом порядке. Трудоемкость заданий: два теоретических вопроса – по 30 минут, две задачи – по 20 минут. Резерв времени на оформление работы и понимание условий заданий – 20 минут. Зачтенной считается работа, где выполнено не менее половины заданий билета, причем решена хотя бы одна задача. Пересдача зачета проводится по таким же билетам и на тех же условиях. Пересдача зачета комиссии проводится в виде теста, где студенту предлагается 20 заданий с выбором варианта ответов (трудоемкость каждого задания – 5 минут).
ПРОГРАММА
письменного зачета по математике для
слушателей ПК
первый семестр
1. Определители и их свойства.
2. Решение систем линейных уравнений. Правило Крамера.
3. Матрицы, действия над матрицами.
4. Обратная матрица.
5. Ранг матрицы.
6. Решение систем линейных уравнений в матричной форме.
7. Теорема Кронекера-Капелли.
8. Векторы, сложение векторов, умножение вектора на скаляр.
9. Прямоугольная система координат, координаты точки и вектора. Длина вектора.
10. Скалярное произведение векторов. Условие перпендикулярности векторов.
11. Векторное произведение векторов. Условие коллинеарности двух векторов.
12. Смешанное произведение векторов. Условие комплпанарности трех векторов.
13. Деление отрезка в заданном отношении.
14. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение плоскости.
15. Уравнение плоскости, проходящей через три заданные точки.
16. Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.
17. Расстояние от точки до плоскости.
18. Уравнение прямой на плоскости с угловым коэффициентом. Уравнение прямой, проходящей через две данные точки.
19. Угол между двумя прямыми на плоскости. Условие коллинеарности и перпендикулярности прямых на плоскости.
20. Канонические и параметрические уравнения прямой в пространстве.
21. Уравнение прямой в пространстве, проходящей через две заданные точки.
22. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности двух прямых в пространстве.
23. Расстояние между двумя прямыми в пространстве..
24. Условия параллельности и перпендикулярности прямой и плоскости. Точка пересечения прямой и плоскости.
25. Канонические уравнения окружности и эллипса.
26. Канонические уравнения гиперболы и параболы.
27.Определение функции. Способы задания функций.
28. Основные элементарные функции и их графики.
29. Определение предела функции в точке. Свойства пределов.
30. Первый замечательный предел.
31. Второй замечательный предел.
32. Сравнение бесконечно малых.
33. Непрерывность функции. Точки разрыва и их классификация.
34. Определение производной, ее механический и геометрический смысл.
35. Дифференциал функции.Применение дифференциала к приближенным вычислениям.
36. Производные высших порядков.
37. Правило Лопиталя.
38. Возрастание и убывание функции.
39. Максимум и минимум функции. Достаточные условия существования экстремума функции.
40. Выпуклость и вогнутость графика функции.Точки перегиба.
41. Асимптоты графика функции.
42. Общая схема исследования функции и построения графиков.
Типовые задачи
1.
Даны две матрицы А=
 и В=
и В= ,
найти: А
,
найти: А![]() В,
В
В,
В![]() А,
А,
![]() .
.
2.
Проверить совместность системы уравнений
 и в случае совместности решить ее: а) по
формулам Крамера; б) матричным способом
и в) методом Гаусса.
и в случае совместности решить ее: а) по
формулам Крамера; б) матричным способом
и в) методом Гаусса.
3.
Проверить совместность системы уравнений
 и в случае совместности решить ее: а) по
формулам Крамера; б) матричным способом
и в) методом Гаусса.
и в случае совместности решить ее: а) по
формулам Крамера; б) матричным способом
и в) методом Гаусса.
4.
Решить однородную систему уравнений
 .
.
5.
Решить однородную систему уравнений
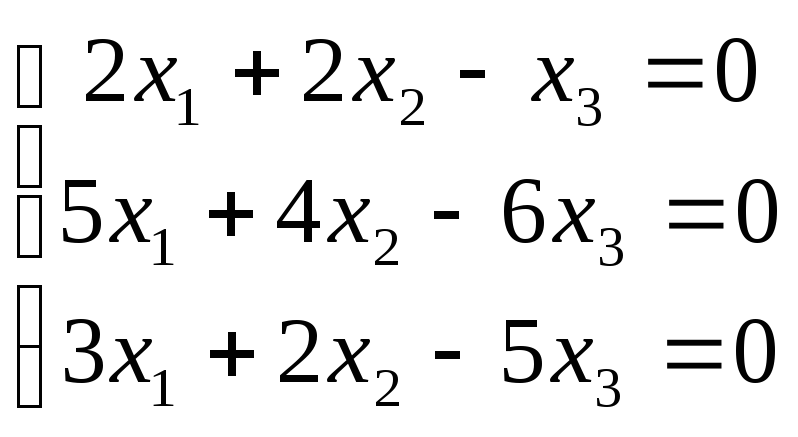 .
.
6.
Даны вершины четырехугольника
![]() .
Вычислить угол
.
Вычислить угол
![]() между его диагоналями.
между его диагоналями.
7.
При каком значении
![]() векторы
векторы
![]() и
и
![]() ортогональны?
ортогональны?
8.
Найти координаты вектора
![]() ,коллинеарного
вектору
,коллинеарного
вектору
![]() ,
если известно, что
,
если известно, что
![]() .
.
9.
В некотором базисе векторы заданы
координатами
![]()
![]() .
Убедиться, что векторы
.
Убедиться, что векторы
![]() образуют
базис и найти в нем координаты вектора
образуют
базис и найти в нем координаты вектора
![]() .
.
10.
Найти координаты вектора
![]() , направленного по биссектрисе угла
между векторами
, направленного по биссектрисе угла
между векторами
![]() и.
и.
![]() .
.
11.
Определить координаты концов А и В
отрезка ,который точками
![]() и
и
![]() разделен на три равные части.
разделен на три равные части.
12.
Дано:
![]() ,
,![]() ,
,![]() ,
вычислить
,
вычислить![]() .
.
13. Вычислить площадь треугольника АВС и длину высоты, проведенной из вершины В , если А(1,2,0);В(3,0,3);С(5,2,6).
14. Даны вершины пирамиды А(2,0,4);В(0,3,7);С(0,0,6);S(4, 3,5).Вычислить ее объем и длину высоты, проведенную из вершины S.
15. Лежат ли точки А(1,2,-1) ;В(4,1,5); С(-1,2,1) ;D(2,1,3) в одной плоскости?
16.
Найти проекцию вектора
![]() на вектор
на вектор
![]() ,
если А(4,6,3);
В(-5,2,6);С(4,-4,-3).
,
если А(4,6,3);
В(-5,2,6);С(4,-4,-3).
17. Найти проекцию точки D(1,0,3) на плоскость, проходящую через точки А(1,2,3);В(2,-1,1); С(4,3,2).
18. Найти проекцию точки D(1,0,3) на прямую, проходящую через точки А(1,2,3);В(2,-1,1);
19.
Составить уравнение плоскости, проходящей
через точку Р(1,0,2) перпендикулярно к
двум плоскостям
![]() .
.
20.
Составить уравнение плоскости,
параллельной вектору
![]() и отсекающей на координатных осях ОХ и
ОУ отрезки а=3 и в= -2.
и отсекающей на координатных осях ОХ и
ОУ отрезки а=3 и в= -2.
21. Найти координаты точки Q,симметричной точке Р(-3,1,-9) относительно плоскости 4х-3у-z-7=0
22. Вычислить расстояние между параллельными плоскостями
x-2y-2z-12=0 ;x-2y-2z-6=0.
23. Написать уравнение плоскости, проходящей через точки М(-1,-2,0) и Р(1,1,2) и перпендикулярной к плоскости х+2у+2z-4=0.
24.
Записать уравнения прямой
![]() в канонической форме.
в канонической форме.
25.
Написать уравнения прямой, проходящей
через точку М(-1,2,-2) параллельно прямой
![]() .
.
26.
Найти расстояние от точки М(3,0,4) до
прямой
![]() .
.
27.
Найти угол между прямой
![]() и
плоскостью 2х+у+z-4=0.
и
плоскостью 2х+у+z-4=0.
28.
Написать уравнение плоскости, проходящей
через прямую
![]() и точку Р(3,4,0 ).
и точку Р(3,4,0 ).
29. Найти проекцию точки М(2,3,4) на прямую х = у = z.
30.
Найти кратчайшее расстояние между
прямыми
![]() и
и
![]() .
.
31.
Упростить уравнение линии и определить
ее вид:
![]() .
.
32.
Упростить уравнение линии и определить
ее вид:
![]() .
.
33.
Упростить уравнение линии и определить
ее вид:
![]() .
.
34.
Упростить уравнение линии и определить
ее вид:
![]() .
.
35. Составить уравнение кривой второго порядка, если расстояние между фокусами равно 6, а эксцентриситет равен 0,6.
36.
Установить взаимное расположение прямой
и плоскости и в случае их пересечения
найти координаты точки пересечения:
![]() и
и
![]() .
.
37.
Установить взаимное расположение прямой
и плоскости и в случае их пересечения
найти координаты точки пересечения
![]() и
и![]() .
.
38.
Установить взаимное расположение прямой
![]() и
плоскости
и
плоскости
![]() и в случае их пересечения найти
координаты точки пересечения.
и в случае их пересечения найти
координаты точки пересечения.
39.
Найти:
![]() .
.
40.
Найти:
![]() .
.
41.
Найти:
![]() .
.
42.
Найти:
![]() .
.
43.
Найти:
![]() .
.
44.
Найти:
![]() .
.
45.
Найти:
![]() .
.
46.
Найти:
![]() .
.
47.
Найти:
![]() .
.
48.
Найти:
![]() .
.
49.
Найти:
![]() .
.
50.
Найти:.
![]() .
.
51.
Найти:
![]() .
.
52.
Найти производную функции![]() ,
заданной неявно.
,
заданной неявно.
53.
Найти производную функции
![]() ,
заданной неявно.
,
заданной неявно.
54.
Найти производную от у по х, если
 .
.
55.
Найти производную от у по х ,если
 .
.
56.
Найти производную от функции у по
аргументу х, если
![]() .
.
57.
Найти производную от функции у по
аргументу х, если
 .
.
58.
Найти производную от функции у по
аргументу х, если
![]() .
.
59.
Вычислить вторую производную функции
![]() .
.
60.
Вычислить вторую производную функции
![]()
61.
Вычислить вторую производную функции
![]() ,заданной
неявно.
,заданной
неявно.
62.
Вычислить вторую производную функции
у по х , если![]() .
.
63.
С помощью дифференциала вычислить
приближенно
 .
.
64.
С помощью дифференциала вычислить
приближенно
![]() .
.
65.
С помощью дифференциала вычислить
приближенно
![]() .
.
66.
Исследовать функцию на непрерывность
и построить ее график, если

67.
Исследовать функцию
![]() на непрерывность в точках
на непрерывность в точках
![]()
68.
Найти предел, используя правило Лопиталя
:![]() .
.
69.
Найти предел, используя правило Лопиталя:
![]() .
.
70.
Найти предел, используя правило Лопиталя
:![]() .
.
71.
Найти предел, используя правило Лопиталя:
![]() .
.
72.
Найти предел, используя правило Лопиталя:
![]() .
.
73.
Найти предел, используя правило Лопиталя:
![]() .
.
74.
Найти предел, используя правило Лопиталя
:![]() .
.
75.
Найти наименьшее и наибольшее значение
функции
![]()
на отрезке [-1/2; 0].
76.
Провести полное исследование функции
![]() и построить её график.
и построить её график.
77.
Провести полное исследование функции
![]() и построить её график.
и построить её график.
78.
Провести полное исследование функции
![]() и построить её график.
и построить её график.
79.
Провести полное исследование функции
![]() и построить её график.
и построить её график.
80.
Провести полное исследование функции
![]() и построить её график.
и построить её график.
81.
Провести полное исследование функции
![]() и построить её график.
и построить её график.
