Информатикаmp3_inf

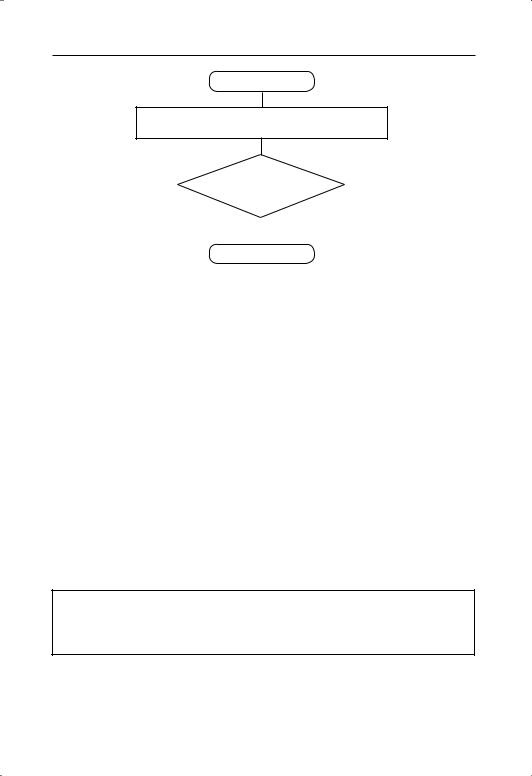
Приложение

Начало

Вычислить цену самой дешёвой — ­ третьей шоколадки

Дохо­ дить­ до пере­мен­ ных­ и чисел­ в этом алго­рит­ ме­ представ­ля­ ет­ ся­ неце­ле­ со­ об­ раз­ ным,­ так как пере­во­ да­ в копей­ки­ число­вые­ исход­ные­ данные­ зада­чи­ и выпол­ня­ е­ мые­ действия не требу­ют,­ а включе­ние­ в алго­ритм­ деталь­ной­ рабо­ ты­ с состав­ной­ имено­ван­ ной­ вели­чи­ ной­ значи­­ тельно­ ослож­нит­ его, и, на наш взгляд, не имеет­ смысла­.

Исполь­зо­ва­ние­ мето­да­ ­ после­до­ва­тель­ной­ дета­ли­за­ции­

При реше­нии­ более­ сложных­ тексто­вых­ задач­ реко­мен­ ­ду­ет­ся исполь­зо­ ­вать метод­ после­до­ ­ва­тель­ной дета­ли­ ­за­ции. Приме­не­ ­ние этого­ мето­да­ помо­га­ ­ет детям­ учиться­ поис­ку­ реше­ния­ зада­чи,­ когда­ оно не очевид­но­ .

Приве­дём­ несколь­ко­ приме­ров­ разно­го­ уровня­ сложнос­ти­ (будем,­ по прежне­ ­му, рассмат­ ­ри­вать зада­ ­чи, алго­ ­рит­мы реше­ ­ния кото­ ­рых содер­жат­ ветвле­ния)­ .

Пример­ 7. Учебник­ Арги­нс­ ­кой И.И., 2 класс, № 409, с. 174 В пункте­ 1) зада­ния­ предла­га­ ­ет­ся решить­ зада­чу:­

Столяр­ почи­нил­ в первый­ день 7 столов,­ во второй­ — в 2 раза­ больше,­ чем в первый,­ а в третий­ — на 2 стола­ меньше,­ чем во вто­ рой. Успел­ ли он закон­чить­ рабо­ ту,­ если­ требо­ва­ лось­ почи­нить­ 41 стол?

В учебни­ке­ мате­ма­ ти­ ки­ из этой зада­чи­ путём­ сниже­ния­ сложнос­ти­ была­ полу­че­ на­ зада­ча­ № 424, рассмот­рен­ ная­ ранее­. Будем­ учить искать­

221

Информатика и ИКТ. 3 класс

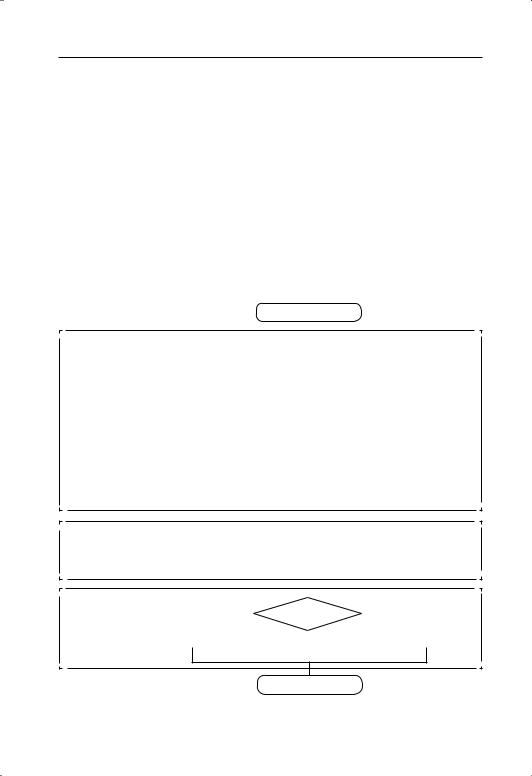
реше­ ние­ такой­ зада­чи­ за счёт состав­ле­ ния­ алго­рит­ ма­ мето­дом­ после­­ дова­ тель­ ной­ дета­ли­ за­ ции­  — в два этапа­.

Запи­ шем­ укруп­нён­ ный­ алго­ритм­ (этап 1).

Нача­ло­

1.Опре­де­ ­лить, сколько­ столов­ чинил­ столяр­ каждый­ день.

2.Вычис­лить,­ сколько­ столов­ почи­нил­ столяр­ за 3 дня.

3.Сравнить­ коли­че­ ­ст­во почи­нен­ ­ных столов­ с коли­че­ ­ст­вом ­ столов,­ кото­рые­ требо­ва­ ­лось почи­нить,­ и отве­тить,­ ­ успел­ ли столяр­.

Конец­

На этапе­ 2 состав­ля­ ем­ блок схему­.

Конец

222

Приложение

Пример­ 8. Учебник­ Петер­сон­ Л.Г., 2 класс, часть 3, № 4, с. 4

В сорев­но­ ва­ ни­ ях­ по стрельбе­ за коман­ду­ школы­ высту­па­ ли­ Алёша, Кирилл­ и Сергей­. Алёша­ набрал­ 250 очков­. Это на 40 очков­ больше,­ чем у Кирил­ла,­ но на 90 очков­ меньше,­ чем у Сергея­. Прошла­ ли их коман­да­ в следу­ю­ щий­ тур, если­ проход­ной­ балл — 750 очков?­

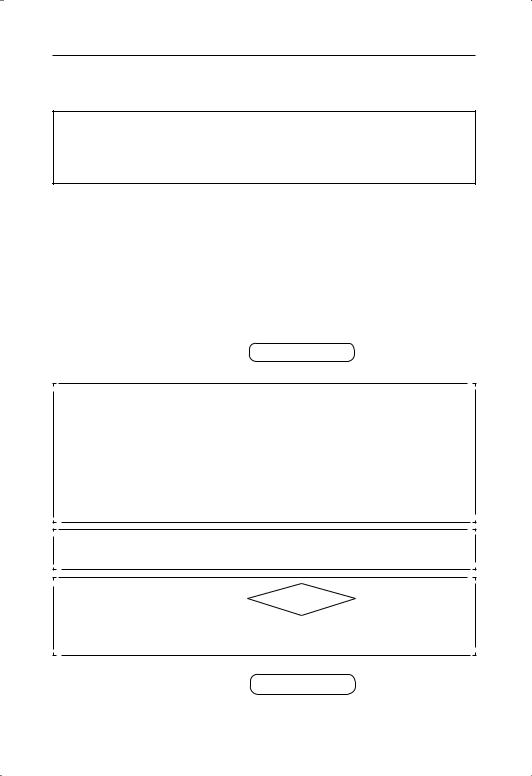
Укруп­ нён­ ный­ алго­ритм­ запи­шем­ так:

Нача­ло­

1.Опре­де­ ­лить, сколько­ очков­ набрал­ каждый­ стрелок­.

2.Вычис­лить,­ сколько­ очков­ набра­ ­ла коман­да­ .

3.Сравнить­ коли­че­ ­ст­во набран­ ­ных очков­ с коли­че­ ­ст­вом ­

требу­е­ ­мых очков­ и отве­тить,­ прошла­ ли коман­да­ .

Конец­

Ему отве­ча­ ет­ блок схема:­

Конец

223

Информатика и ИКТ. 3 класс

Пример­ 9. Учебник­ Арги­нс­ кой­ И.И., 3 класс, № 358, с. 158

Поми­до­ ры­ укла­ды­ ва­ ют­ ся­ в одина­ко­ вые­ ящики­ поров­ну­ . В семи­ ящиках­ поме­ща­ ет­ ся­ на 32 кг больше­ поми­до­ ров,­ чем в трёх. Хватит­ ли для уклад­ки­ 872 кг поми­до­ ров­ 120 ящиков?­

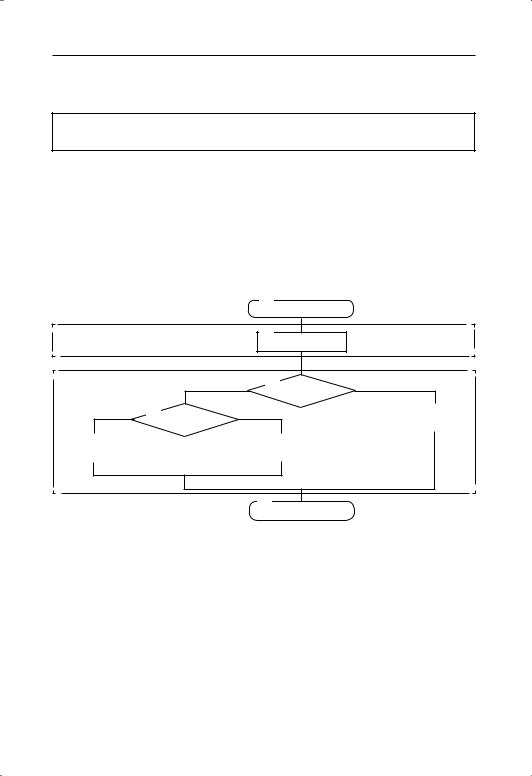
Укруп­ нён­ ный­ алго­ритм­ может­ быть пример­но­ таким:­

Нача­ло­

1.Узнать,­ сколько­ поми­до­ ­ров (в кг) поме­ща­ ­ет­ся в один ящик (А).

2.Вычис­лить,­ сколько­ поми­до­ ­ров (в кг) поме­ща­ ­ет­ся ­ в 120 ящиках­ (В).

3.Сравнить­ резуль­тат­ (В) с задан­ным­ (в кг) коли­че­ ­ст­вом поми­­ доров­ (872) и дать ответ,­ хватит­ ли ящиков­.

Конец­

Пример­ный­ вид блок схемы:­

Конец

224

Приме­ча­ние­. Если­ дети­ соста­вят­ алго­ритм­ самос­то­ ­я­тель­но, они могут­ не учесть, что звери­ быва­ют­ и одно­го­ возрас­та,­ и поэ­то­ ­му вклю­ чить в него­ только­ один блок провер­ки­ усло­вия­ . Выяс­ни­ ­те причи­ну:­ не поду­ма­ ­ли о таком­ вари­ан­ ­те или сравни­ли­ возраст­ уже при состав­ле­ ­нии алго­рит­ ­ма. В первом­ случае­ доста­точ­ ­но испра­вить­ ошибку,­ во вто­ ром — очень важно­ объяс­нить,­ что в процес­се­ состав­ле­ ­ния алго­рит­ ­ма вычис­ле­ ­ния не произ­во­ ­дят­ся.

Отме­тим­ также,­ что в правиль­ном­ самос­то­ ­я­тель­но состав­лен­ ­ном алго­рит­ ­ме усло­вия­ могут­ быть и иными­. Напри­мер,­ в блоке­ 5 можно записать А = 14, обме­няв­ содер­жи­ ­мое блоков­ 6 и 7. Подоб­ные­ возмож­­ ности­ будут­ и в других­ алго­рит­ ­мах.

225

Информатика и ИКТ. 3 класс

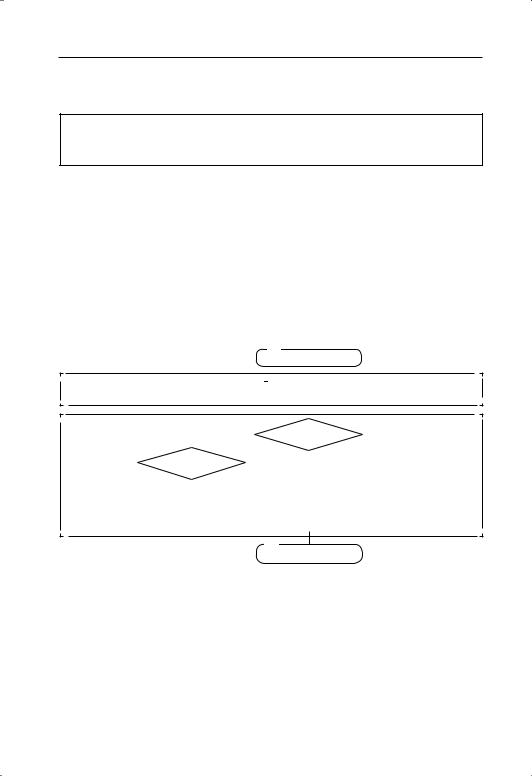
Пример­ 11. Учебник­ Петер­сон­ Л.Г., 2 класс, часть 2, № 4, с. 48 Зада­ние­ содер­жит­ зада­чу­ в одно­ действие:

Водном­ паке­те­ 15 шоко­лад­ ­ных конфет­ и 38 ирисок,­ а в дру­ гом — 26 шоко­лад­ ­ных конфет­. Каких­ конфет­ больше­ в этих паке­тах:­ шоко­лад­ ­ных или ирисок?­

Взада­че­ требу­ет­ ­ся опре­де­ ­лить, каких­ конфет­ больше­ в двух паке­­ тах вместе­.

Укруп­нён­ ­ный алго­ритм­ можно­ запи­сать­ так:

Нача­ло­

1.Вычис­лить­ А — коли­че­ ­ст­во шоко­лад­ ­ных конфет­ ­ в двух паке­тах­ вместе­.

2.Сравнить­ коли­че­ ­ст­во шоко­лад­ ­ных конфет­ с коли­че­ ­ст­вом ирисок­ (38) и дать ответ­.

Конец­

Блок схема­ алго­рит­ ­ма может­ быть такой:­

1

8

Конец

Приме­ча­ние­. При самос­то­ я­ тель­ ной­ рабо­ те­ над алго­рит­ мом­ не все дети­ учтут,­ что коли­че­ ст­ во­ разных­ конфет­ может­ совпасть,­ и поэ­то­ му­ не включат­ блоки­ 5 и 6. Возмож­ные­ ситу­а­ ции:­

1)случай­ность­ или ошибка,­ кото­рую­ доста­точ­ ­но испра­вить;­

2)вычис­ле­ ­ния в процес­се­ состав­ле­ ­ния алго­рит­ ­ма, недо­пус­ ­ти­мость кото­рых­ необ­хо­ ­ди­мо объяс­нить­ детям;­

3)созна­ ­тель­ное исклю­ ­че­ние раве­ ­н­ства в силу­ пони­ ­ма­ния, что сумма­ нечёт­но­ ­го и чётно­го­ чисел­ равна­ нечёт­но­ ­му числу­ (а 38 — чётное­ число)­ .

226

Приложение

В этом случае­ упро­щён­ный­ алго­ритм­ ребён­ка­ следу­ет­ признать­ верным,­ но пояс­нить,­ что ал­горитм­ обычно­ стремят­ся­ сделать­ таким,­ чтобы­ при изме­не­нии­ исход­ных­ данных­ доста­точ­но­ было­ заме­нить­ в нём числа­.

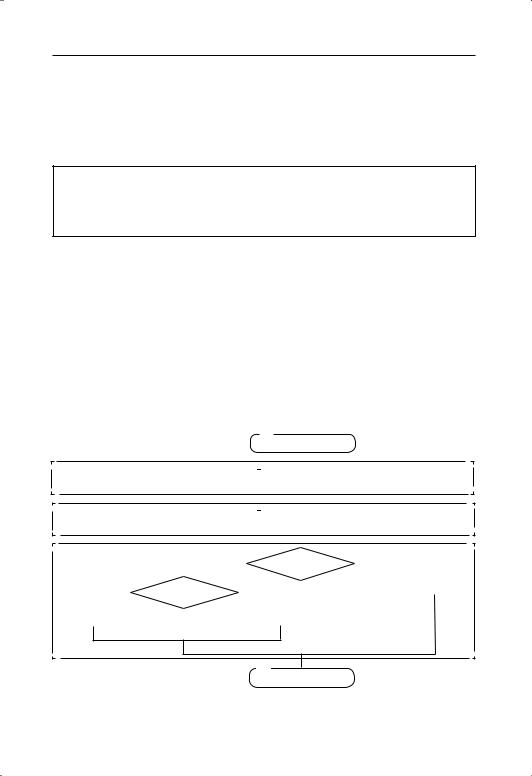
Пример­ 12. Учебник Чекина А.Л., 3 класс, часть 2, № 143, с. 52 Задание содержит задачу с вычислением площадей:

Миша и Маша красили пол в доме у бабушки. Миша красил в комнате, длина которой 5 м, а ширина — 3 м. Маша красила на веранде, которая имеет квадратную форму со стороной 4 м. Кто из них сделал бо′льшую работу?

Укрупнённый алгоритм, цель которого — определить, кто сделал бо′льшую работу, и сформулировать ответ, можно записать так:

Начало

1.Вычислить площадь комнаты.

2.Вычислить площадь веранды.

3.Сравнить площади и дать ответ.

Конец

Составим блок схему (через K обозначена площадь комнаты в квадратных метрах, через V — площадь веранды):

9

Конец

227

Информатика и ИКТ. 3 класс

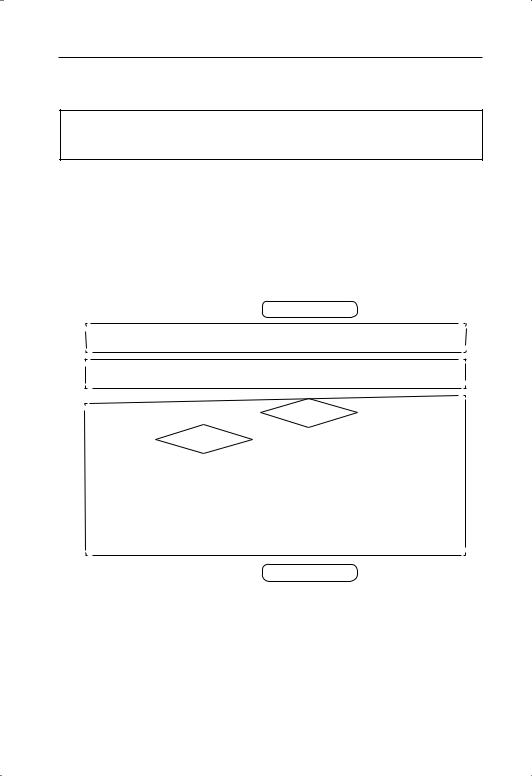
Пример­ 13. Учебник­ Арги­нс­ кой­ И.И., 3 класс, № 308, с. 135 Зада­ние­ содер­жит­ зада­чу­ на движе­ние­ .

Один путе­ше­ ст­ вен­ ник­ был в пути­ 8 дней и прохо­дил­ в день 28 км, а другой­ путе­ше­ ст­ во­ вал­ 9 дней и прохо­дил­ в день 25 км. Кто из них прошёл­ бо′льший­ путь и на сколько?­

Укруп­ ­нён­ный алго­ритм­ может­ быть пример­но­ таким:­

Нача­ло­

1.Вычис­лить­ А — путь 1 го путе­ше­ ­ст­вен­ни­ка (в км).

2.Вычис­лить­ В — путь 2 го путе­ше­ ­ст­вен­ни­ка (в км).

3.Сравнить­ А и В, опре­де­ ­лить их разность­ С и напи­сать­ ответ­.

Конец­

Блок схема­ может­ выгля­ ­деть так:

Начало

Конец

Приме­ча­ние­. Если­ дети­ разра­ба­ ты­ ва­ ют­ алго­ритм­ самос­то­ я­ тель­ ­ но, высо­ка­ веро­ят­ ность,­ что многие­ не учтут­ возмож­ность­ прохож­де­ ния­ одина­ко­ во­ го­ пути,­ и соот­ве­ т­ ствен­ но­ включат­ только­ один блок провер­­ ки усло­вия­ . Возмож­ные­ ситу­а­ ции:­

1)случай­ность­ или ошибка,­ кото­рую­ доста­точ­ ­но испра­вить;­

2)вычис­ле­ ­ния в процес­се­ состав­ле­ ­ния алго­рит­ ­ма, недо­пус­ ­ти­мость кото­рых­ необ­хо­ ­ди­мо объяс­нить­ детям;­

228

Приложение

3) учёт особен­нос­ тей­ число­вых­ данных,­ когда­ ребё­нок­ созна­тель­ но­ исклю­ча­ ет­ вари­ант­ раве­н­ ства,­ пони­мая,­ что произ­ве­ де­ ние­ чётных­ чисел­ (значит,­ чётное­ число)­ не может­ равнять­ся­ произ­ве­ де­ нию­ нечёт­ных­ чисел (то есть нечёт­но­ му­ числу)­ . В этом случае­ упро­щён­ ный­ вари­ант­ не счита­ет­ ся­ ошибоч­ным,­ но необ­хо­ ди­ мо­ пояс­нить,­ что алго­ритм­ обычно­ делают­ таким,­ чтобы­ при изме­не­ нии­ исход­ных­ данных­ доста­точ­ но­ было­ заме­нить­ в нём числа­.

Пример­ 14. Учебник­ Арги­нс­ кой­ И.И., 3 класс, № 139, правая­­ зада­ча,­ с. 64

Зада­ние­ содер­жит­ состав­ную­ зада­чу:­

В киос­ке­ было­ 493 тетра­ди­ в клетку­ и 504 тетра­ди­ в линей­ку­ . Каких тетра­дей­ оста­лось­ меньше­ и во сколько­ раз, когда­ прода­ли­ 486 тетра­дей­ в клетку­ и 469 в линей­ку?­

Приве­дём­ укруп­нён­ ный­ алго­ритм­ и блок схему:­

Нача­ло­

1.Вычис­лить­ А — коли­че­ ­ст­во остав­ших­ ­ся тетрадей в клетку­.

2.Вычис­лить­ В — коли­че­ ­ст­во остав­ших­ ­ся тетрадей в линей­ку­ .

3.Сравнить­ А и В, опре­де­ ­лить частное­ С и напи­сать­ ответ­.

Конец­

Начало

229

Информатика и ИКТ. 3 класс

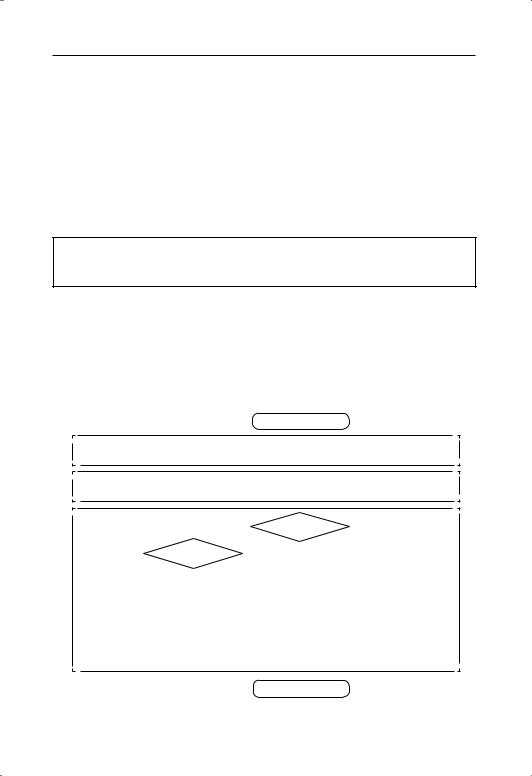
Пример­ 15. Учебник­ Петер­сон­ Л.Г., 2 класс, часть 3, № 6, с. 85 Зада­ние­ содер­жит­ состав­ную­ зада­чу:­

Дональд­ Дак пошёл­ в терра­ри­ ум­ . Там он увидел­ чере­пах,­ ящериц­ и змей. Всего­ он насчи­тал­ 230 живот­ных­ . Чере­пах­ было­ 24,­ а ящериц­ — в 3 раза­ больше,­ чем чере­пах­ . Кого­ больше­ было­ тер­ рари­у­ ме­  — змей или ящериц,­ и на сколько?­

Укруп­ нён­ ный­ алго­ритм­ может­ быть пример­но­ таким:­

Нача­ло­

1.Вычис­лить­ А — число­ ящериц­.

2.Вычис­лить­ В — число­ змей.

3.Сравнить­ А и В, опре­де­ ­лить их разность­ С и напи­сать­ ответ­.

Конец­

Приве­дём­ блок схему­ (через­ S обозна­че­ но­ общее­ коли­че­ ст­ во­ яще­ риц и чере­пах)­ .

230