II этап: Решение задачи на эвм средствами пакета Excel

1. Формируем диапазон ячеек с исходными данными А1:F7 (см. рис. 22).

2. Определяем ячейки, в которых будут содержаться переменные (неизвестные) задачи B11:E13.

Примечание: Диапазон неизвестных удобно оформить в виде таблицы.

Присваиваем неизвестным произвольные значения, например, предполагаем, что от каждого завода к каждому объекту необходимо перевезти 1 усл. ед. кирпича (см. рис. 22).

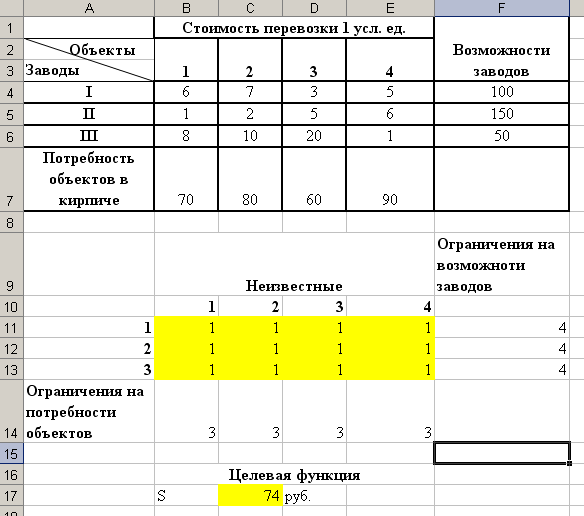
Рис.22 Оформление задачи в Excel

3. Вводим формулу в ячейку, где будет находиться значение целевой функции С17 (см. рис. 23).

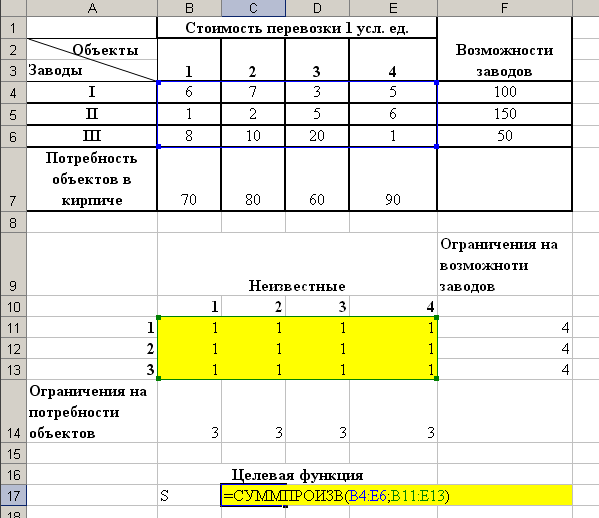
Рис.23 Ввод целевой функции

Примечание: Для удобства ввода рекомендуется воспользоваться функцией СУММПРОИЗВ() (Перемножает соответствующие элементы заданных массивов и возвращает сумму произведений.).

Аргументами функции являются массив со стоимостями перевозок В4:Е6 и массив с неизвестными В11:Е13.

4. Вводим зависимости для ограничений (см. рис.24).

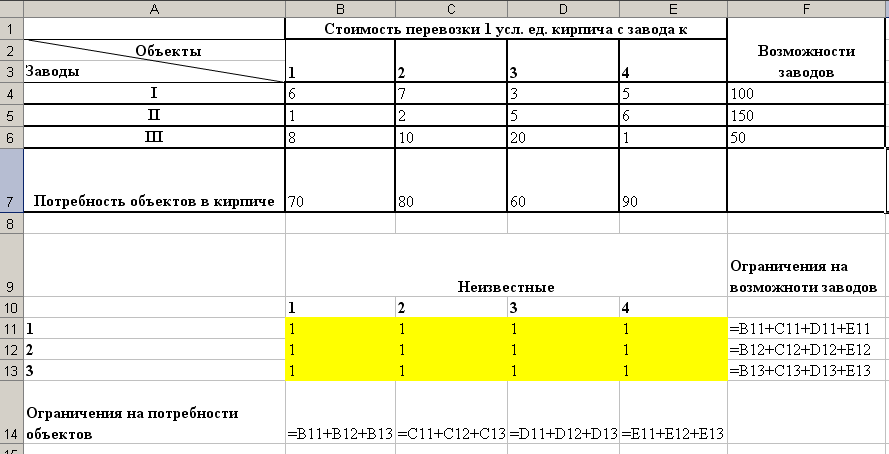
Рис.24 Ввод ограничений

Примечание: В ячейках F11:F13 и B14:E14 занесены левые части ограничений, правые части ограничений содержаться в ячейках F4:F6 и B7:E7.

Примечание: Ограничения 20 и 21 будут учтены в окне Поиск решения.

5. Для получения численного решения задачи используем инструмент Поиск решения (Сервис/Поиск решения).

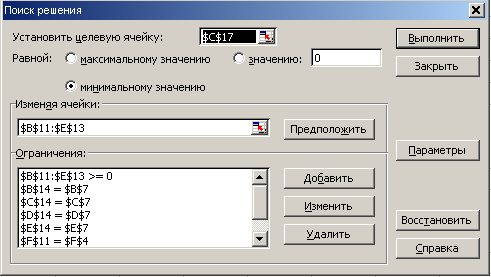
Рис.25 Поиск решения

• В окне Установить целевую ячейку указываем адрес ячейки с целевой функцией С17.

• В разделе Равной указать Минимальному значению.

Примечание: Для заполнения окна Установить целевую ячейку необходимо на листе выделить ячейку, в которой содержится значение целевой функции.

• В окно Изменяя ячейки вносим адреса ячеек с неизвестными задачи B11:E13.

Примечание: Для ввода неизвестных можно нажать кнопку Предположить.

• Для ввода ограничений необходимо перейти в поле Ограничения и нажать кнопку Добавить. В появившемся диалоговом окне Добавление ограничения, последовательно, для каждого неравенства в разделе Ссылка на ячейку указать адрес ячейки, соответствующей левой части ограничения, а в разделе Ограничения – адрес правой части ограничения.

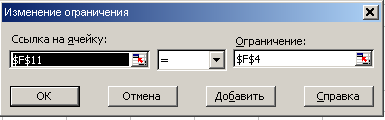
Рис. 26 Ввод ограничения 1

Примечание: Ограничения 14-19 вводятся аналогично

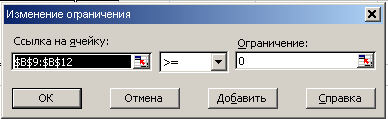
Рис. 6 Ввод ограничения 8

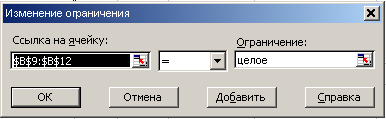
Рис. 7 Ввод ограничения 9

• Нажать кнопку Выполнить.

Ответ

В результате решения задачи был получен следующий ответ:

x11=0 (с первого завода на первый объект кирпичи не поставляются),

x12=0 (с первого завода на второй объект кирпичи не поставляются),

x13=60 (с первого завода на третий объект необходимо поставить 60 усл ед. кирпичей),

…

X34=50 (с третьего завода на четвертый объект необходимо поставить 50 усл. ед. кирпичей),

.

При этом минимальная стоимость перевозки будет 660 руб., .

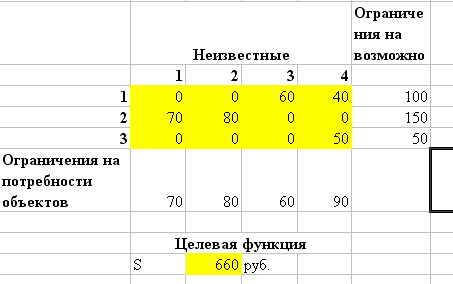
Рис. 29 результат решения задачи

1.3.2.2 Открытая транспортная задача Постановка задачи

Изменим условие задачи 4 следующим образом: допустим, что потребность первого завода в кирпиче возросла вдвое и составила 140 ед. кирпича в день. Остальные данные остались неизменными.

Таблица 12

	Стоимость перевозки 1 усл. ед. кирпича с завода к строящемуся объекту				Возможности заводов
Объекты Заводы	1	2	3	4
I	6	7	3	5	100
II	1	2	5	6	150
III	8	10	20	1	50
Потребность объектов в кирпиче	140	80	60	90

Данная задаче уже является открытой, т.к. 140+80+60+9>100+150+50, т.е. потребности превышают запасы на 160 ед.

Введем нового поставщика - IV завод с возможностью 160 ед.

Так как груз от фиктивного поставщика к фиктивному потребителю не перевозится, то стоимость перевозок полагается равной нулю.

Таблица 12 примет вид:

Таблица 13

	Стоимость перевозки 1 усл. ед. кирпича с завода к строящемуся объекту				Возможности заводов
Объекты Заводы	1	2	3	4
I	6	7	3	5	100
II	1	2	5	6	150
III	8	10	20	1	50
IV	0	0	0	0	160
Потребность объектов	140	80	60	90

Данная задача уже является закрытой и решается аналогично задаче

Применение транспортных моделей к решению экономических задач

Алгоритм и методы решений транспортной задачи могут быть применены для решения некоторых классов экономических задач. К таким задачам относятся:

• Задача о назначениях. Она позволяет определить какой механизм и на какую работу надо назначить, чтобы добиться максимальной производительности или минимизировать затраты времени.

• Задача о закреплении самолетов за воздушными линиями.

• Оптимальное закрепление за станками операций по обработке деталей и др.