3 Анализ моделей

Для сравнения нормированных корреляционных функций воспользуемся критерием среднего квадратичного отклонения по первым 10 отсчетам. , где

–выборочная нормированная корреляционная функция исходного процесса, – рассчитанная теоретическая нормированная корреляционная функция для модели АРСС (M,N):

, где

- параметры модели АРСС(M,N),

- выборочная нормированная корреляционная функция исходного процесса.

Для модели СС(0) теоретическая нормированная корреляционная функция будет подсчитываться по формуле:

Для модели АР(3):

Для модели АРСС(2,3):

Результаты сравнения выборочной и теоретических нормированных корреляционных функций представлены в Таблице 3:

Таблица 3 – Оценка качества моделей АРСС через СКО

M	N
	0	1	2	3
0	1,9921948	-	-	-
1	4,1844862	-	-	-
2	0,0009685	0,0007573	0,0001302	0,0000005
3	0,0008266	-	0,0007394	0,0000135

Теперь смоделируем 3 выборки по наилучшим моделям АР(M), СС(N) и АРСС(M,N).

Алгоритм моделирования:

1. Генерируем случайный вектор из 6000 компонентов, имеющих стандартный нормальный закон распределения (белый шум). Для этого воспользуемся стандартной функцией пакета Scilab:

Y=grand(6000,1,'nor',0,1).

2. Преобразуем каждый компонент вектора по формуле:

, где

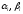- параметры модели АРСС(M,N),

- белый шум,

- выборочное среднее исходного процесса.

считая элементы с отрицательными индексами нулевыми.

3. Отбрасываем первую 1000 компонент как брак.

Выборочные нормированные корреляционные функции рассчитываются по формуле:

, где

–соответствующие компоненты вектора смоделированного процесса,

- исправленная выборочная дисперсия:

, где

–соответствующие компоненты смоделированного вектора ,

– выборочное среднее,

– объем выборки.

– выборочное среднее:

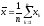, где

–соответствующие компоненты смоделированного вектора ,

– объем выборки;

– объем выборки.

Теперь построим графики теоретических и выборочных нормированных корреляционных функций для указанных наилучших моделей, коими являются, как видно из таблицы 3, модели АРСС(0,0) (СС(0)), АРСС(3,0) (АР(3)) и АРСС(2,3), и изобразим их на рисунках 3-5. Рисунок 2 – Теоретическая нормированная корреляционная функция для модели СС(0)

Рисунок 3 – Теоретическая нормированная корреляционная функция для модели АР(3)

Рисунок 4 – Теоретическая нормированная корреляционная функция для модели АРСС(2,3)

4 Спектральная плотность мощности

Спектральная плотность мощности связывается с корреляционной функцией так:

Для построенных моделей АРСС найдем оценку теоретической спектральной плотности мощности по формуле:

Изобразим построенную оценку и теоретическую спектральную плотность мощности на рисунках 5-7.

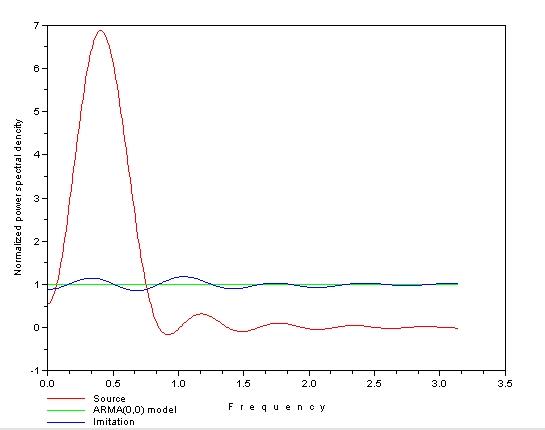
Рисунок 5 – Спектральная плотность мощности для модели СС(0)

Рисунок 6 – Спектральная плотность мощности для модели АР(3)

Рисунок 7 – Спектральная плотность мощности для модели АРСС(2, 3)

5 Моделирование

Теперь изобразим фрагменты реализаций исходного и смоделированных процессов

графически на рисунках 8-11.

Рисунок 8 – Фрагмент реализации исходного случайного процесса

Рисунок 9 – Фрагмент реализации сгенерированного случайного процесса по модели СС(0)

Рисунок 9 – Фрагмент реализации сгенерированного случайного процесса по модели АР(3)

Рисунок 9 – Фрагмент реализации сгенерированного случайного процесса по модели АРСС(2,3)

Как видно, лучшие результаты показали модели АРСС(2,3) и АР(3). Это и следовало ожидать из оценки ошибки по критерию среднего квадратичного отклонения теоретических корреляционных функций по первым 10 отсчетам.