3 Анализ моделей

Будем анализировать качество построенных моделей, сравнивая их нормированную корреляционную функцию с оценкой нормированной корреляционной функции исходного процесса. Для сравнения возьмём первые 10 значений нормированных корреляционных функций и для каждой модели вычислим среднее квадратическое отклонение.

Результаты вычислений занесём в таблицу 3.

Таблица 3 – Оценка качества моделей АРСС через СКО

M	N
	0	1	2	3
0	0.1758	0.1694	0.0298	0.0020
1	0.1744		-	0.0020
2	0.0292	0.0182	0.0040	0.0020
3	0.0262		-	0.0015

В таблице тёмно-бирюзовым цветом отмечена лучшая модель АРСС, а серым цветом – лучшие модели из классов АР и СС. Как и следовало ожидать, это модели АРСС(3, 3), АР(3) и СС(3) соответственно. Видно также, что все модели с СС-составляющей равной 3 оказались очень неплохими, чего нельзя сказать о соответствующих моделях с АР-составляющей равной 3.

Теперь построим графики теоретических нормированных корреляционных функций для указанных наилучших моделей и изобразим их на рисунках 2, 3 и 4 соответственно. Будем считать, что для всякой модели АРСС(M, N) (N+M+1) значение нормированной корреляционной функции совпадает, а остальные значения отыщем из системы:.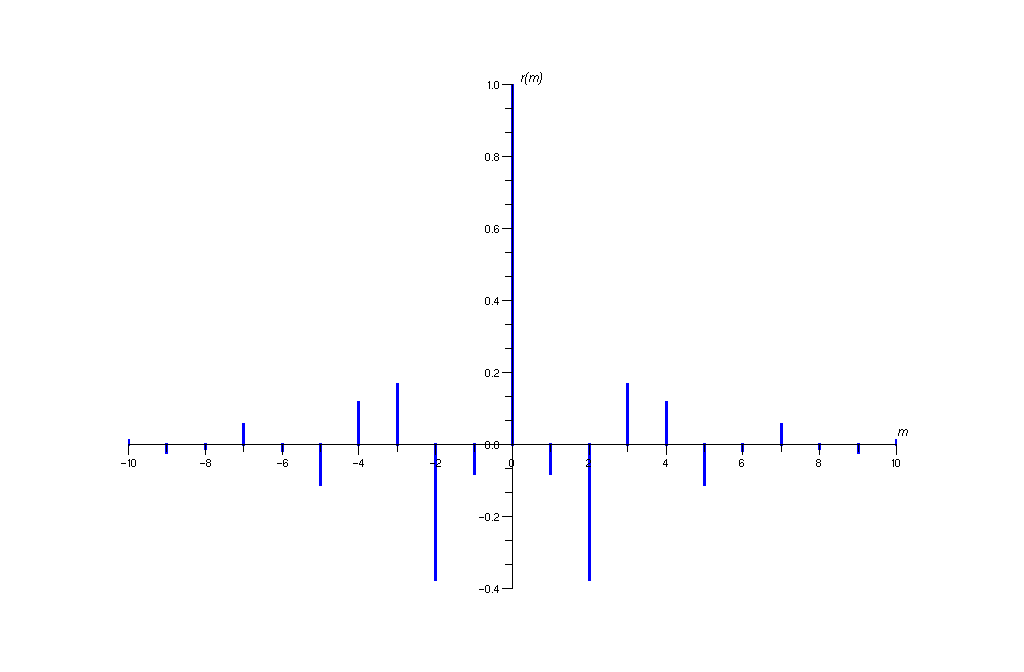Рисунок 2 – Теоретическая нормированная корреляционная функция для модели АР(3)

Рисунок 3 – Теоретическая нормированная корреляционная функция для модели СС(3)

Рисунок 4 – Теоретическая нормированная корреляционная функция для модели АРСС(3, 3)

Смоделируем три процесса на основе лучших моделей, руководствуясь формулой из таблицы 2. Белый шум будем генерировать как последовательность из копий случайной величины, распределённой по нормальному закону с нулевым математическим ожиданием и единичной дисперсией. Несколько первых значений генерируемого случайного процесса положим нулевыми как основание рекурсии. Чтобы придать новому процессу нужное математическое ожидание (непосредственно после генерации оно близко к нулю), просто прибавим его к каждому отсчёту. Таким образом сгенерируем 6000 отсчётов, после чего отбросим первую 1000 как брак.

Построим ещё 3 рисунка, разместив на каждом из них график выборочной нормированной корреляционной функции исходной выборки, график параметрической оценки нормированной корреляционной функции для соответствующей модели и график выборочной нормированной корреляционной функции для сгенерированного по этой модели процесса. На рисунке 5 изобразим соответствующий график для модели АР(3), на рисунке 6 – для модели СС(3), а на рисунке 7 – для АРСС(3, 3). Чтобы 3 графика не слишком мешали друг другу, придётся изобразить их линейную интерполяцию. При этом следует помнить, что на самом деле нормированные корреляционные функции дискретных процессов определены только в целых координатах, а всё остальное – это просто их линейное продолжение, которое сделано исключительно для наглядности.

Рисунок 5 – Анализ нормированной корреляционной функции модели АР(3)

Рисунок 6 – Анализ нормированной корреляционной функции модели СС(3)

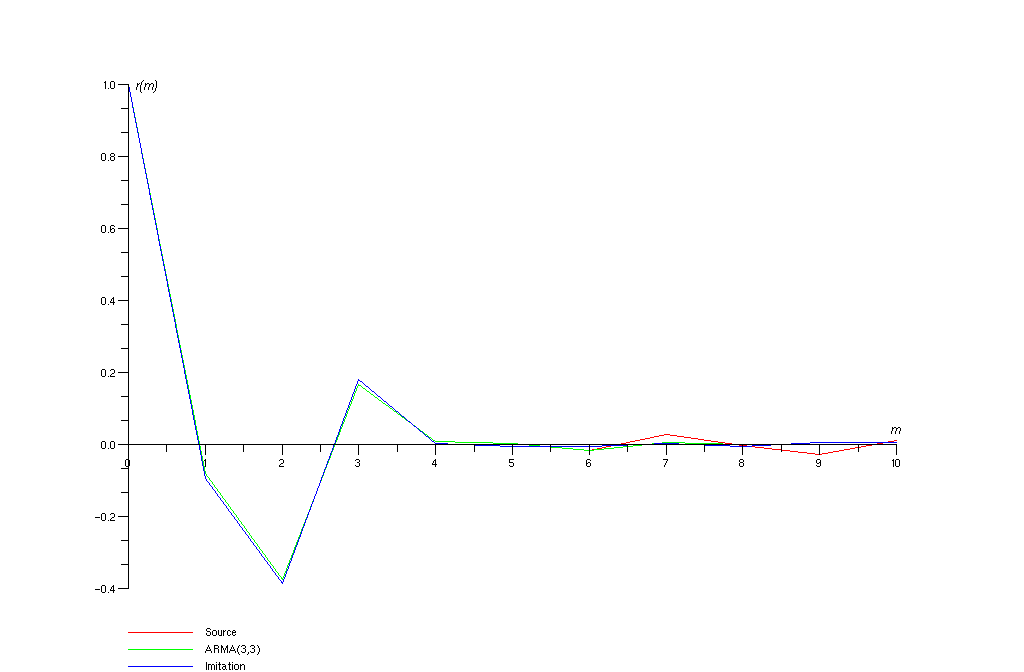
Рисунок 7 – Анализ нормированной корреляционной функции модели АРСС(3, 3)

На этих рисунках красные линии – выборочные нормированные корреляционные функции исходной выборки, зелёные – параметрические оценки нормированных корреляционных функций моделей, синие – выборочные нормированные корреляционные функции соответствующих смоделированных процессов.