3 Анализ моделей

Будем анализировать качество построенных моделей, сравнивая их нормированную корреляционную функцию с оценкой нормированной корреляционной функции исходного процесса. Для сравнения найдем первые 10 значений корреляционных функций. Будем считать, что для всякой моделипервыезначений нормированной корреляционной функции совпадаютc соответствующими значениями корреляционной функции исходной выборки, а остальные значения отыщем из системы:

Для модели АР(3):

Для модели СС(2):

Для модели АРСС (3,3):

Таблица 3 – Первые 10 значений нормированных корреляционных функций лучших моделей

Нормированная корреляционная функция для модели АР(3)
1.0000	0.6370	0.2487	0.1674	0.1870
0.1463	0.0820	0.0497	0.0412	0.0330
Нормированная корреляционная функция для модели СС(2)
1.0000	0.6370	0.2487	0.0000	0.0000
0.0000	0.0000	0.0000	0.0000	0.0000
Нормированная корреляционная функция для модели АРСС(3,3)
1.0000	0.6370	0.2487	0.1674	0.1812
0.1361	0.0654	0.0303	0.0267	0.0245
Нормированная корреляционная функция исходной выборки
1.0000	0.6370	0.2487	0.1674	0.1812
0.1361	0.0654	0.0349	0.0314	0.0167

Для каждой модели вычислим среднее квадратическое отклонение

где – рассчитанная теоретическая нормированная корреляционная функция для модели АРСС(M,N)

Результаты вычислений занесём в таблицу 3.

Таблица 4 - Оценка качества моделей АРСС через СКО

M	N
	0	1	2	3
0	0.5538	–	0.0862	–
1	0.0346	0.0461	0.0089	–
2	0.1092	–	­	0.0271
3	0.0019	0.0011	0.0011	0.0007

В таблице синим цветом отмечена лучшая модель АРСС, а зеленым цветом – лучшие модели из классов АР и СС. Это модели АРСС(3, 3), АР(3) и СС(2) соответственно. Видно также, что все модели с АР-составляющей равной 3 оказались очень неплохими, чего нельзя сказать о соответствующих моделях с СС-составляющей равной 3.

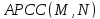
Теперь построим графики теоретических нормированных корреляционных функций для указанных наилучших моделей и изобразим их на рисунках 2, 3 и 4 соответственно. Будем считать, что для всякой модели значение нормированной корреляционной функции совпадаетc соответствующим значением корреляционной функции исходной выборки, а остальные значения отыщем из системы:

Рисунок 2 – Теоретическая нормированная корреляционная функция для модели АР(3)

Рисунок 3 – Теоретическая нормированная корреляционная функция для модели CC(2)

Рисунок 4 – Теоретическая нормированная корреляционная функция для модели АРСС(3,3)

4 Спектральная плотность мощности

Спектральная плотность мощности связывается с корреляционной функцией так:

Для построенных моделей АРСС найдем оценку теоретической спектральной плотности мощности по формуле:

где

Таким образом, спектральные плотности мощностей для лучших моделей АР, СС и АРСС будут выглядеть следующим образом:

Изобразим построенную оценку и теоретическую спектральную плотность мощности на рисунках 5-7.

Рисунок 5 – Спектральная плотность мощности для модели АР(3)

Рисунок 6 – Спектральная плотность мощности для модели СС(2)

Рисунок 7 – Спектральная плотность мощности для модели АРСС(3,3)