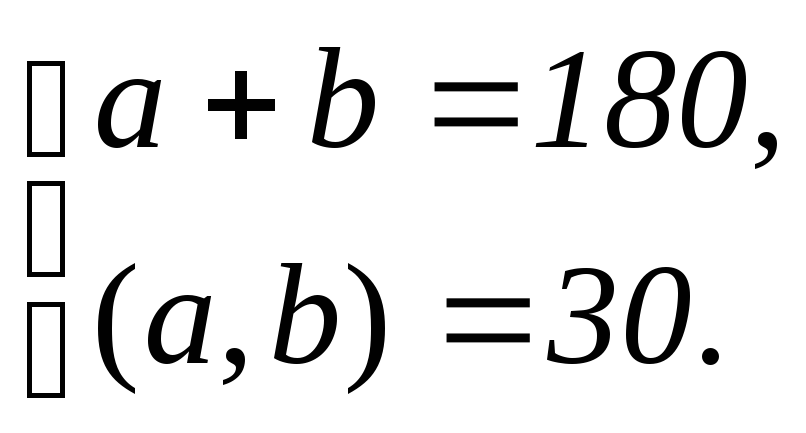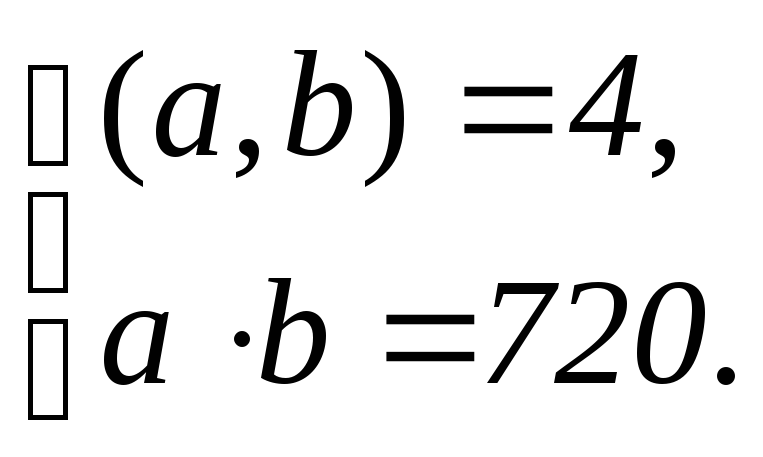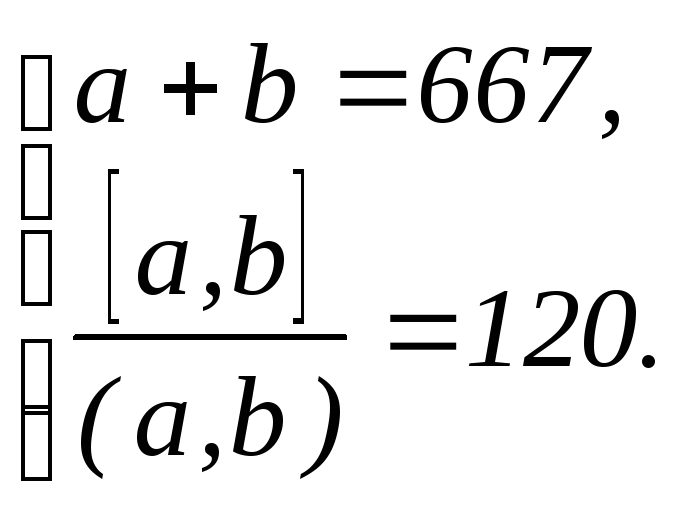Практическое занятие 4. Маршруты графа. Связные графы.

Контрольные вопросы:

1. Маршрут графа.

2. Матрица маршрутов.

3. Теорема о нахождении маршрутов длины kграфа.

4. Достижимая вершина графа.

5. Матрица достижимости.

6. Нахождение матрицы достижимости графа.

7. Матрица контрдостижимости.

8. Связь между матрицами достижимости и контрдостижимости графа.

9. Критерий взаимной достижимости вершин графа.

10. Матрица сильных компонент графа.

План занятия.

1. Теоретический диктант.

2. Проверка домашнего задания.

3. Решение типовых задач.

Номер задания	Аудиторная работа	Домашняя работа
1	1)	2)
2	1)	2)

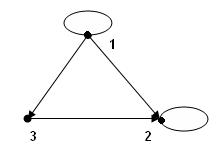
Задание 1.Для графаG найти:

а) матрицу маршрутов длины k;

б) найти все маршруты длины k.

1) G: 2)G:

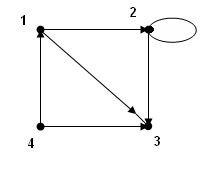k=3 k=4

Задание 2.Для графаG найти все сильные компоненты.

1) G: 2)G:

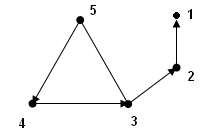
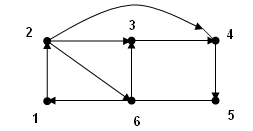
Практическое занятие 5. Метрические характеристики связных графов.

Контрольные вопросы:

1. Матрица расстояний графа.

2. Расстояние между вершинами графа.

3. Эксцентриситет вершины графа.

4. Диаметр связного неорграфа.

5. Радиус связного неорграфа.

6. Периферийная вершина.

7. Центральная вершина.

План занятия.

1. Теоретический диктант.

2. Самостоятельная работа.

3. Проверка домашнего задания.

4. Решение типовых задач.

Номер задания	Аудиторная работа	Домашняя работа
1	1)	2)

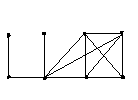
Задание 1.Для графаGнайти:

а) матрицу расстояний;

б) эксцентриситеты всех вершин;

в) диаметр и радиус;

г) периферийные вершины;

д) центральные вершины.

1) G: 2)G:

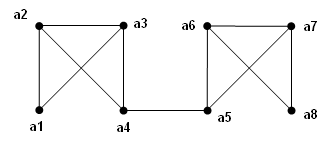
Практическое занятие 6. Нод и нок целых чисел. Алгоритм Евклида. Линейное представление нод.

Контрольные вопросы:

1. Определение отношения делимости двух чисел.

2. Деление с остатком.

3. Теорема о делении с остатком.

4. НОД целых чисел.

5. Алгоритм Евклида.

6. Теорема о линейном представлении НОД.

7. НОК целых чисел.

8. Теорема о нахождении НОК двух целых чисел.

9. Взаимно простые числа.

10. Каноническое представление натурального числа.

11. Теорема о нахождении НОД и НОК целых чисел с помощью канонического представления.

План занятия.

1. Теоретический диктант.

2. Проверка домашнего задания.

3. Решение типовых задач.

Номер задания	Аудиторная работа	Домашняя работа
1	1),2)	3),4)
2	1),2)	3),4)
3	1)	2),3)

Задание 1.Даны целые числаaиb. Найти:

а) наибольший общий делитель aиb;

b) линейное представление наибольшего общего делителяaиb;

с) наименьшее общее кратное aиb.

1. a=2576, b=154.

2. a=1073, b=3683.

3. a=2585, b=7975.

4. a=4598, b=1474.

Задание 2.Найти натуральные числа aиb, если:

1. 

2. 

3. 

Задание 3. Разложить на простые множители числоn!, если

1. n=45.

2. n=35.

3. n=40.

Практическое занятие 7. Числовые функции.

Контрольные вопросы:

1. Числовые функции.

2. Число всех натуральных делителей натурального числа.

3. Сумма всех натуральных делителей натурального числа.

4. Число всех натуральных чисел, меньших n и взаимно простых с n.

5. Теорема о каноническом разложении числа .

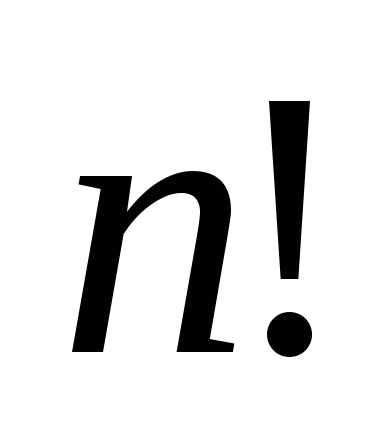План занятия.

1. Теоретический диктант.

2. Проверка домашнего задания.

3. Решение типовых задач.

Номер задания	Аудиторная работа	Домашняя работа
1	1),2)	3),4)
2	2)	1),3)

Задание 1.Для натурального числаnнайти:

1. число τ(n) всех натуральных делителей;

2. сумму σ(n) всех натуральных делителей;

3. количество φ(n) натуральных чисел, меньшихnи взаимно простых сn.

1. n=1542.

2. n=1440.

3. n=1575.

4. n=1404.

Задание 2.

1. Найти наименьшее натуральное число, имеющее 12натуральных делителей.

2. Найти натуральное число, которое делится на два простых числа, если число его натуральных делителей равно 6, а их сумма –28.

3. Найти количество натуральных чисел, меньших числа 1476и имеющих с ним наибольшим общим делителем число41.