А) Расчет по сНиП п-23-81*

Отношение жесткостей на 1 м длины ригеля и стойки n равно:

Изгибающие моменты в угловых сечениях 1 и 7 будут следующими:

от вертикальной нагрузки q (рис. 2, а настоящего приложения):

, кН×м;

от горизонтальной нагрузки Т (рис. 2, б настоящего приложения):

кН×м.

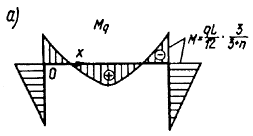
Рис. 2. Эпюры изгибающих моментов

а - от вертикальной нагрузки; б - от горизонтальной нагрузки Т; в -от лишней неизвестной Х

Коэффициенты расчетной длины m стойки определим по формуле (70, б) СНиП П-23-81* при р = п= 0,624:

.

В соответствии с п. 5.27* СНиП II-23-81* определяем:

относительный эксцентриситет ;

отношение площади полки к площади стенки: A_f/A_w= 048;

коэффициент влияния формы сечения h= 1,51;

приведенный относительный эксцентриситет m_ef = mh = 2,40;

гибкость стойки l= 71,5;

условную гибкость .

По табл. 74 СНиП II-23-81* принимаем коэффициент снижения расчетных сопротивлений j_е= 0,329.

Из формулы (51) СНиП II-23-81* находим расчетное значение параметра нагрузки P_d:

.

Б) Проверка области применения настоящих рекомендаций

Проверим условие (1):

.

Условие (1) выполнено, следовательно, раму можно рассчитывать на основе настоящего Пособия.

В) Вычисление параметра критической нагрузки Pе

Условие потери устойчивости рамы по антисимметричной форме имеет вид трансцендентного уравнения [19] - относительно параметра устойчивости v, равного

,

где - нормальная сила в стойке при Р = 1, равная

.

Первый (низший) корень трансцендентного уравнения при п = 0,624 равен v = 2,1. Соответствующее ему значение параметра критической нагрузки P_e будет равно

Г) Определение параметра нагрузки краевой текучести материала Ру

Согласно п. 5 настоящего приложения основной системой заданной свободной рамы будет соответствующая несвободная рама с фиктивной опорой от горизонтального смещения в уровне ригеля, которая полностью воспринимает горизонтальную нагрузку Т и не воспринимает вертикальную нагрузку q. Поэтому эпюра изгибающих моментов в основной системе рамы будет равна M_o = М_q (см. рис. 2, а настоящего приложения), а эпюра изгибающих моментов от лишней неизвестной z (горизонтального смещения рамы) будет равна М_z=М_r (см. рис. 2, б настоящего приложения).

Наиболее напряженным поперечным сечением, в котором возникает первый пластический шарнир, является правое опорное сечение ригеля. По формулам (10) и (9) настоящего приложения находим:

Д) Определение параметра нагрузки пластической усталости Pa

Наибольший размах напряжений Ds имеет место в крайнем внутреннем волокне концевого сечения правой стойки. В этом волокне наибольшее сжимающее напряжение s_тах имеет место при сочетании нагрузок q(P), V(P) и Т(Р), а наименьшее сжимающее (или наибольшее растягивающее) напряжение s_min - при сочетании нагрузок q(0,5P), V(0,5P) и Т(-Р). По формулам пп. 5 и 6 вычисляем:

кН×м;

кН×м;

кН×м;

кН×м;

м.

Согласно п. 6 настоящего приложения параметр нагрузки пластической усталости Р_a вычисляется при нормативных значениях нагрузок. Примем среднее значение коэффициента перегрузки k= 1,2.

.

е) Построение кривой предельного равновесия “в большом” Р_р = Р_р (h)

Для иллюстрации применим оба метода предельного равновесия: статический и кинематический. В силу симметрии рамы и нагрузки будем рассматривать только верхнюю половину рамы. В соответствии с эпюрами моментов M_q (рис. 2, а) и М_r (рис. 2, б) примем безразмерные координаты расчетных поперечных сечений i такими: 0; 0,1; 0,2; 0,3; 0,4; 0,5; 1,0.