Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Альметьевский государственный нефтяной институт

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Тесты по математике

.pdf

Скачиваний:

219

Добавлен:

15.05.2015

Размер:

1.12 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Найти сумму коэффициентов разложения подынтегральной дроби

	x 2 + 4
ò	x 2 (x - 8)dx

Вычислить определённый интеграл

ò x 4 dx

−1

Вычислить определённый интеграл

1 dx

0ò 1 + x

Вычислить определённый интеграл

-1

x 3

-2

Вычислить определённый интеграл

x - 2

Вычислить определённый интеграл

ò4 cos2 x dx

Вычислить определённый интеграл

−3

25 + 3x

												о	т			е			к
2

					- 1									1
							2				и			2
							2							2
0					48			4							4
					48		5							5
							5							5
ln 2				и	б				л					0
			б		ln3
	5		б		-		3							3
	5						3							3

	8						8							8
аяπ 1					π		1							π			1
16					-	16								1
3							3
8 +					- 8 -								- 8 +
8 +		4			- 8 -					4			- 8 +					4
1					0									-			2
														-			3
																	3

4815

−ln 2

- 85

π8 - 14

Вычислить определённый интеграл

e2	dx
eò
eò	x ln x

Вычислить определённый интеграл

1 x3dx

0ò x8 +1

Вычислить определённый интеграл

ò2 sin x ×cos2 x dx

Вычислить определённый интеграл

ò5 хх 2 -16dx

Вычислить определённый интеграл

π / 2

ò(x + 3) sin xdx

Вычислить определённый интеграл

ò1

x2 + 2x

Вычислить

xdx

ò0 1+ 3x

Вычислить

ò1

3x - 2

Вычислить определённый интего

ал

ò0

(2x +1)3

										о	т	е		к
											т	е
-1							0					1
									и
		π				π		л	и		-		π
8					16			л				16
0				и	б		1					1
0							1					1
			б									3
												3
9							1					0
9							1					0
ая					-4							2
0					-4							2
		ln2			5ln3						0,5ln1,5
8							4				-4
1		ln13			ln13						13
	3	ln13
2							9					2
												9
52
52

ln 2

-π8

-13

-9

Вычислить определённый интеграл

πò

сos

cos

Вычислить определённый интеграл

ò1

x 2 + 5x + 4

Вычислить площадь фигуры,

ограниченной линиями

y = 4x − x 2 , y = 0

Вычислить площадь фигуры,

ограниченной линиями

y = −x 2 , x = 1, x = −1, y = 0

Вычислить площадь фигуры,

ограниченной линиями

y = ln x, y = 0, x = e

Вычислить площадь фигуры,

ограниченной линиями

y3 = x, y = 1, x = 8

Вычислить площадь фигуры,

ограниченной линиями

y = −x 2 , y = x − 2, y = 0

Вычислить площадь фигуры,

ограниченной линиями

y = x 2 − 2, y = x

														о	т		е	к
															т		е
			1				-2						и			0
	1	ln		5				1	ln 5				и				5
	1			5				1									5
	3			4				3								4
												л
	−		32				б					л				64
			3			и				3						3
			1		б	и				2						0
			1							2						0
			3							3
			3							3
			1				2e −1									e −1
ая
			1				4				1					4
											4
			1							1							1
			3							6						2
4,5								− 4,5								1,5

− 13

№

Текст задания

Вычислить	ò5	xdxò1		ydy
	3		0
Вычислить	ò4	dxò3	(x − y)dy
	1	1
Вычислить	ò2	dxò1	(х2 + y)dy
	1	0
	π	π
Вычислить	ò2	dxò2	sin(x + y)dy
	0	0
Вычислить	ò4	dxò2		dy
Вычислить	ò4	dxò2			2
	3	1 (x + y)
	ln 2	2x
Вычислить òdx òe x+ y dy
	0	x
Вычислить	2	2−x
Вычислить	òdx ò(х − y)dy
	0	0
Вычислить	2	х2
Вычислить	òdx ò(2х − у)dy
	1	х
Вычислить	1	2− х2
Вычислить	ò dx ò			(х − y)dy		т
	−3 2х−1					т
	−3 2х−1
Вычислить	ò3	dx2òх (х + 2y)dy
	2	х		е	к
	2	х

		Тема 8. Кратные интегралы													о
															о
													Варианты
					3							0		и
					1							2	л
					4							2
										и	б
					0				б		-4
					0				б		-2
					0						-2
						ая
				25							ln	25
				24								24
				н	0							5
				н								6
												6
			н		0						-2
	о				0						0,9
р
р				4	4							4
					15						15
				25			1				25
				25			3					3
							3					3
								54
								54

е		к
е
т
тветов
	3
	-4
	-3
	2	5
	2	6
		6
	2

ln 25

4		5
0
-2
4	5
	6

4

2		2x
Вычислить ò xdx		ò ydy
0	−		2x
4		y+4
Вычислить ò ydy			ò xdx
−2	0,5 y 2
0	y2
Вычислить òdy ò(x + 2y)dx
2	0
2π				2+cosϕ
Вычислить òsin ϕ dϕ					ò ρ dρ
0					1
0,5π					2 cosϕ
Вычислить ò	sin ϕdϕ				ò ρdρ
0					0
Вычислить площадь области,
ограниченной линиями:
у 2 = х +1, х + у = 1
Вычислить площадь области,
ограниченной линиями:
х 2 = у, у = 4, 4у = х2
Вычислить площадь области,
ограниченной линиями:
у 2 = х + 4, х + 3у = 0
Вычислить площадь области,
ограниченной линиями:
у = х2 − 2х, у = х

			т	р
Вычислить площадь области,
ограниченной линиями:
у 2 = 4 − х, х + 2у = 4	е	к
у 2 = 4 − х, х + 2у = 4

			90			-30
			30			90			л
			-11						л
			-11			-11,2
			0			б
			0		и	-1
			2	б	и	3
			2			3
			4,5			-4
			ая
			10			10		2
	н	н	20				5
о	н					6
						6
			4			3
			4			-4,5

и	о	т

е	к
0

112

20 56

-90

126

4,5

21Вычислить площадь области, ограниченной линиями:

у= 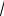х, у = 0, х = 4

22Вычислить площадь области, ограниченной линиями:

у = 2х 2 −1, х = у

23Вычислить площадь области, ограниченной линиями:

у= sin x, у = 0, x = 0, x = π

24Вычислить площадь области, ограниченной линиями:

у = −2 + 3х − x 2 , у = 0

25Вычислить площадь фигуры,

ограниченной линиями

	х = у 2 − 2у, х + у = 0
26	Изменить порядок интегрирования

	1	1−x2
	ò dx	ò f (x, y)dy
	−1	0
27	Изменить порядок интегрирования

	1	y						о
	òdy ò f (x, y)dx
	0	y
	0	y
28	Изменить порядок интегрирования
		ò1	dx3òx	f (x, y)dy		т	р
		ò1	dx3òx	f (x, y)dy
		0	2x
		0	2x
				е	к
				е

		16
				9
		8
		2
		6
				1
		3
						ая
1		1− y 2
ò dy			ò f (x, y)dx
0	н
0	−		1− y2
1		1− y 2
ò dy			ò f (x, y)dx
0	−		1− y		2
н	−		1− y
	2		2х
	òdy ò fdx +
	0		х
	3	1
	òdy ò fdx
	2		2х
					56


		16
			3			и
		0				и
		9			л
	и	б			л
	и	б
б		1
б				1
				1
		6

	3	1− y 2
	òdy	ò f (x, y)dx
	0	1− y 2

ò1 dх òх f (x, y)dу

0 х2

ò2 dyò2 f (х, у)dx

0 y


о	т	е						к

							3
		5
		27
		27
		2,25
						1
		6
		3

	1		1− y2
	ò dy			ò f (x, y)dx
	−1	−		1− y 2
	1	х2
	òdх ò f (x, y)dу
	0	− х
					y
	2	2
	ò dхò fdу +
	0				y
		3
	3	1
	ò dхò fdу
	2				y
		3

1		1− y2
òdх			ò f (x, y)dу
0	−		1− y 2
х2	1
òdyò f (x, y)dx

х0

	y
2	2

òdyò fdx +

ò3 dyò1 fdx

29	Изменить порядок интегрирования
	3	3− y
	òdy ò fdx
	0	0
30	Изменить порядок интегрирования
	ò1	dxòx	fdy + ò2	dx2ò− x fdy
	0	0	1	0
31	Изменить порядок интегрирования
	4	2
	òdxò fdy
	1	1
32	Изменить порядок интегрирования
	ò4		y
	ò4	dy ò fdx
	0	−	y
33						2	4− у
	Областью интегрирования òdу òdх
						0	у
	является
34						2	5
	Областью интегрирования òdу òdх
	является					0	у−2
	является							о
35						1	3	о
35						1	3
	Областью интегрирования òdxòdy
						0	р
						0	−1
	является					т
				е	к

												о	т			к
3		3−x				5		2−x						3	3
3		3−x				5		2−x						3	3
ò	dx	ò	fdy			ò	dx		ò	fdy				òе	ò	fdy
	dx		fdy				dx			fdy				dx		fdy
0		0				0			0		и			0	0
3		3−x				3		2− y						3 2−x
òdx		ò	fdy			òdy			ò	fdx				òdx	ò	fdy
0		0				0	б		0	л				0	0
0		0				0			0					0	0
4		2				2			4					2	2
òdxò fdy					и	òdуò fdх								òdуò fdх
1		1			и	1			1					1	1
1		1				1			1					1	1
4		2		б		2			4					2	4
òdxò fdy				б		ò fdyòdx								òdx ò fdy
0		0				−2			0					−2	x2
		ая			прямоугольник								треугольник
квадрат					прямоугольник								треугольник
н	круг						ромб							трапеция
	круг						ромб							трапеция
	круг						ромб						прямоугольник

3 3− у

òdу ò fdх

0	0
1	2− y

òdy ò fdx

0 y

2 4

òdxò fdy

1 1

ò4 dy ò2 fdx

x −2

круг

квадрат

36	Областью интегрирования
	1		1−х2
	òdx			òdy является
	−1	−		1−х2
37							3	5х
	Областью интегрирования òdx òdy
	является						1	2х
38	является
38							2	3х
	Областью интегрирования òdx òdy
	является						0	х / 2
39	является
39							4	3
	Областью интегрирования òdxòdy
	является						0	1
	является
40							−2	2х
	Областью интегрирования òdx òdy
	является						−10	0
	является
41							2	х+3
	Областью интегрирования òdx òdy
	является						−1	1	о
							−1	1
								р
					е	к	т	р

							о	т	е	к
								т	е
	круг			ромб					квадрат
трапеция					л	и			ромб
					л	и
				квадрат
квадрат				б					ромб
квадрат			треугольник						ромб
	круг	б	и					прямоугольник
	круг	параллелограмм						прямоугольник
	ая			квадрат					ромб
треугольник				квадрат					ромб
н
н				квадрат				треугольник
прямоугольник				квадрат				треугольник

треугольник

круг

прямоугольн

ик

квадрат

круг

трапеция

Вычислить тройной интеграл по области, ограниченной поверхностями:

òòò(x + y - z)dxdydz;

V x = -1, x = 1, y = 0, y = 1, z = 0, z = 2

Вычислить тройной интеграл по области, ограниченной поверхностями:

òòò(xy)dxdydz;

V x = 1, x = 2, y = -2, y = -1, z = 0, z =

Вычислить тройной интеграл по области, ограниченной поверхностями:

òòòzdxdydz;

V x = 0, y = 0, z = 0, x + y + z = 1

Вычислить тройной интеграл по

области, ограниченной
поверхностями:				р
òòò(xy)dxdydz;			т	р
òòò(xy)dxdydz;			т
V x2 + y2 = 1, z =	0, z = 1 (x ³ 0, y ³ 0)
	е	к
	е

0,5

о	н	н

24ая

б	и

-2

б1

	и	о	т
л		о

е	к
2

- 241

- 98

- 18

Вычислить тройной интеграл по области, ограниченной поверхностями:

xyzdxdydz;

òòòV x = 0, y = 0, z = 0, x2 + y2 + z2 = 1 (x ³ 0, y ³ 0, z ³ 0)

Вычислить тройной интеграл по области, ограниченной поверхностями:

òòòyzdxdydz;

V x2 + y2 + z2 = 1, z ³ 0

Вычислить тройной интеграл по области, ограниченной поверхностями:

òòò(4x + 3y + 2z +1)dxdydz;

V x = 0, x = 1, y = 0, y = 2, z = 0, z = 3

Вычислить объём тела,					о
ограниченного поверхностями:
2x + 3y + 4z = 12, x = 0, y =		0, z = 0
2x + 3y + 4z = 12, x = 0, y =		0, z = 0
Вычислить объём тела,				р
ограниченного поверхностями:
2z = x2 + y2 , z = 2			т
е	к		т
	к

										о	т	е	к
			1				1						0


		24				48			и
		24				48
		-2				б		л					2
						б		л
					и	0
			ая	б	и
						48
													48
													1
		54											1
н	н	12				-12							0
		4				0							4π

−1 4

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.05.201528.16 Кб53тест 1 экономика отрасли.doc
#
01.05.202528.17 Кб0Тест итоговый.docx
#
21.09.2019102.19 Кб47тест по экономике.docx
#
18.03.2016149.5 Кб20Тесты КЭТ 1.doc
#
01.05.202545.89 Кб0тесты по аудиту - копия.docx
#
15.05.20151.12 Mб219Тесты по математике.pdf
#
01.05.202528.77 Кб0Тесты по Стратегическому менеджменту.docx
#
15.05.2015166.91 Кб68Тесты по теплоэнеретике.doc
#
01.04.2025606.72 Кб3ТЕСТЫ ПО ЭНЕРГОСБ..doc
#
01.09.201961.95 Кб4Техника тенниса.doc
#
01.04.2025305.15 Кб0техническая эксплуат 2.doc