6. В чём состоит суть метода определения момента инерции на трифилярном подвесе.

.

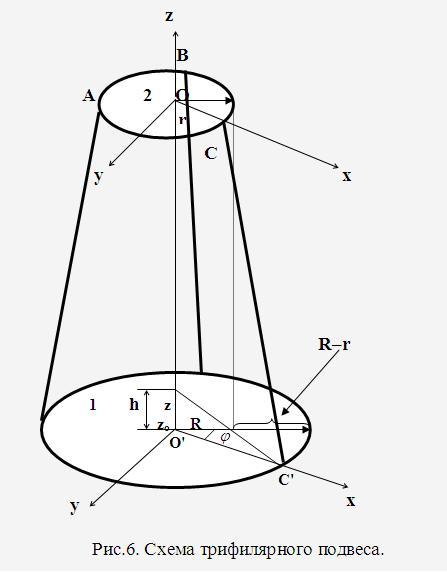
Одним из методов определения моментов инерции твердых тел, является метод крутильных колебаний, осуществляемый с помощью трифилярного подвеса (Рис.6), который состоит из платформы 1, подвешенной на трех симметрично закрепленных нитях к неподвижно закрепленному диску 2 меньшего диаметра. Центры масс диска 2 и платформы 1 находятся на одной оси ОО', относительно которой платформе можно сообщить крутильные колебания, при этом центр тяжести платформы точки О' перемещается по этой оси.

(ОСТАЛЬНОЕ В ОТДЕЛЬНОМ ДОКУМЕНТЕ!!)

Лабораторная работа № 2

1. Колебания. Гармонические колебания. Уравнения гармонических колебаний.

Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.

Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

или

,

где х— значение изменяющейся величины,t— время,

остальные параметры - постоянные: А— амплитуда колебаний,ω— циклическая частота колебаний,— полная фаза колебаний,— начальная фаза колебаний.

Обобщенное гармоническое колебание в дифференциальном виде

Любое нетривиальное решение этого дифференциального уравнение - есть гармоническое колебание с циклической частотой ω.

2. Параметры гармонических колебаний.

Амплиту́да— максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении. Неотрицательная скалярная величина, размерность которой совпадает с размерностью определяемой физической величины.

Циклическая частота колебаний- связана с частотой колебаний соотношением. Единица циклической частоты — радиан в секунду (рад/с,rad/s). В механике при рассмотрении вращательного движения аналогом циклической частоты служит угловая скорость.

Период колеба́ний— наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние, в котором она находилась в первоначальный момент, выбранный произвольно).

3. Маятник математический (теория).

Математическим маятникомназывается материальная точка, подвешенная на нерастяжимой невесомой нити, совершающая колебательное движение в одной вертикальной плоскости под действием силы тяжести.

Таким маятником можно считать тяжелый шар массой m, подвешенный на тонкой нити, длина l которой намного больше размеров шара. Если его отклонить на угол α (рис.7.3.) от вертикальной линии, то под влиянием силы F – одной из составляющих веса Р он будет совершать колебания. Другая составляющая , направленная вдоль нити, не учитывается, т.к. уравновешивается силой натяжения нити. При малых углах смещенияи, тогда координату х можно отсчитывать по горизонтальному направлению. Из рис.7.3 видно, что составляющая веса, перпендикулярная нити, равна

Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

Для вывода закона движения математического и физического маятников используем основное уравнение динамики вращательного движения

Момент силы относительно точки О: , и момент инерции:M = FL. Момент инерцииJв данном случае Угловое ускорение:

С учетом этих величин имеем:

или

(7.8)

Его решение ,

где и

(7.9)

Как видим, период колебаний математического маятника зависит от его длины и ускорения силы тяжести и не зависит от амплитуды колебаний.

4. Виды колебаний (свободные, затухающие, вынужденные), примеры.

Свободные (или собственные) колебания  — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегдазатухающие).

Простейшими примерами свободных колебания являются колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс видав природе невозможен.

Вынужденные колебания  — колебания, протекающие в системе под влиянием внешнего периодического воздействия.

Примеры: листья на деревьях, поднятие и опускание руки. При вынужденных колебаниях может возникнуть явление резонанса: резкое возрастание амплитуды колебаний при совпадении собственной частоты осциллятора и частоты внешнего воздействия.