
Контрольная работа № 3 по теме: «Функции многих переменных».
Задание 1. Найти дифференциал второго порядка данных функций.
2. Найти частные производные неявной функции
27.
![]()
28.
![]()
29.
![]()
30.
![]()
Задание 3. Найти градиент функции в точке М.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 4.
Найти
производную функции
![]() в
точке А по направлению к точке В.
в
точке А по направлению к точке В.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задание 5. Найти уравнения касательной плоскости и нормали к поверхности в заданной точке М.
Задание 6. Найти экстремумы функции двух переменных.
Контрольная работа № 4 по теме « Интегральное исчисление функций».
I. Найти неопределенный интеграл
1.
а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
2.
а) ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
3.
а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
4.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
5.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
6.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
7.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
8.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
9.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
10.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
11.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
12.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г).
;
г).![]()
13.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
14.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
15.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
16.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
17.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
18.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
19.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
20.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
21.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
22.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
23.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
24.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
25.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
26.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
27.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
28.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
29.
а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
30.а)![]() ;
б).
;
б).![]() в)
в)![]() ;
г)
;
г)![]() .
.
II. Найти неопределенный интеграл
1.![]() .
11.
.
11.
![]() .
.
2.
![]() .
12.
.
12.
![]()
3.
![]() .
13.
.
13.
![]() .
.
4.
![]() .
14.
.
14.
![]() .
.
5.
![]() .
15.
.
15.
![]() .
.
6.
![]() .
16.
.
16.
![]()
7.
![]() .
17.
.
17.
![]()
8.
![]() .
18.
.
18.
![]()
9.
![]() .
19.
.
19.
![]() .
.
10.
![]() .
20.
.
20.
![]() .
.
21.
![]() .
26.
.
26.
![]() .
.
22.
![]() .
27.
.
27.
![]()
23.
![]() .
28.
.
28.
![]() .
.
24.
![]() .
29.
.
29.
![]() .
.
25.
![]() .
30.
.
30.
![]() .
.
III.Вычислить определенный интеграл
1.а)![]() ; б)
; б) ;
;
2.а)![]() ;
б)
;
б)
 ;
;
3.а)
![]() ;
б)
;
б)
 ;
;
4.
а) ;
б)
;
б)

5.
а) ;
б)
;
б)
![]()
6.а)
![]() ;
б)
;
б)
 ;
;
7.а)
![]() ;
б)
;
б)

8.а)
![]() ;
б)
;
б)

9.а)
![]() б)
б)
 ;
;
10.а)
![]() ;
б)
;
б)

11.а)
 ;
б)
;
б)

12.
а)![]() ;
б)
;
б)

13.а)
![]() ;
б)
;
б)

14.а)
![]() ;
б)
;
б)

15.а)
![]() ;
б)
;
б)
![]()
16.а)
![]() ;
б)
;
б)

17.а)
![]() ;
б)
;
б)

18.а)
![]() ;
б)
;
б)

19.а)
![]() ;
б)
;
б)

20.а)
![]() ;
б)
;
б)

21.а)
 ;
б)
;
б)

22.а)
![]() ;
б)
;
б)

23.а)
 ;
б)
;
б)
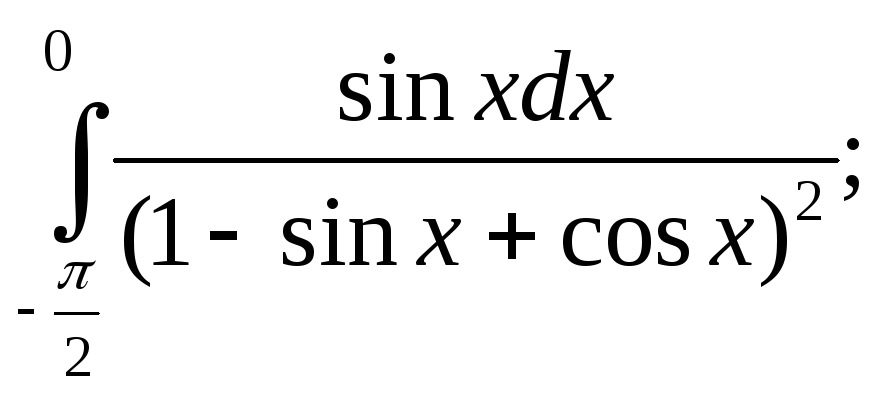
24.а)
![]() ;
б)
;
б)

25.а)
![]() ;
б)
;
б)

26.а)
![]() ;
б)
;
б)

27.а)
![]() ;
б)
;
б)

28.а)
![]() ;
б)
;
б)

29.а)
 ;
б)
;
б)

30.а)
![]() ;
б)
;
б)

IV.А) Вычислить площадь плоской фигуры, ограниченной линиями. Сделать чертеж.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
5.
![]() .
.
6.
![]() .
.
7.
![]() .
.
8.
![]()
9.
![]() .
.
10.
![]() .
.
11.
![]() .
.
12.
![]()
13.
![]()
14.
![]() .
.
15.
![]()
16.
![]() .
.
17.
![]()
18.
![]()
19.
![]() .
.
20.
![]() .
.
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
б) Найти длину дуги кривой, заданной параметрически
1.
 2.
2.

3.
 4.
4.
 .
.
5.
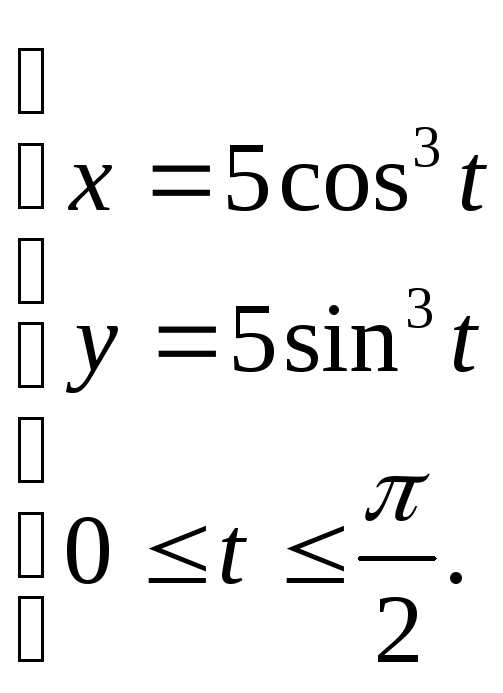 .
6.
.
6.

7.
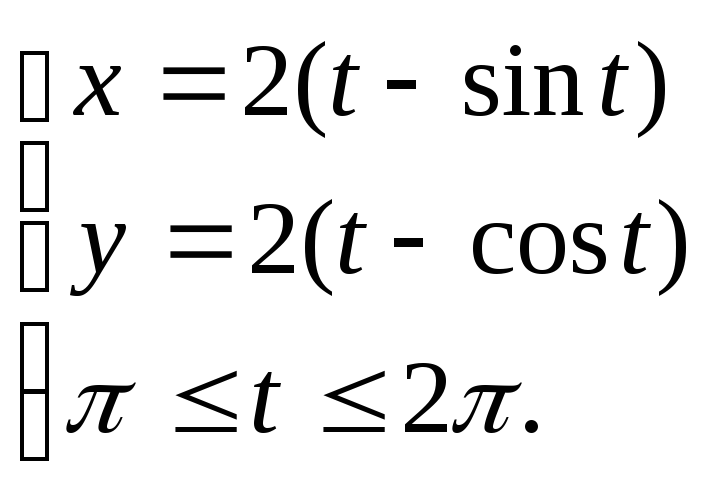 8.
8.
 .
.
9.
 10.
10.
 .
.
11.
 12.
12.

13.
 14.
14.

15.
 16.
16.
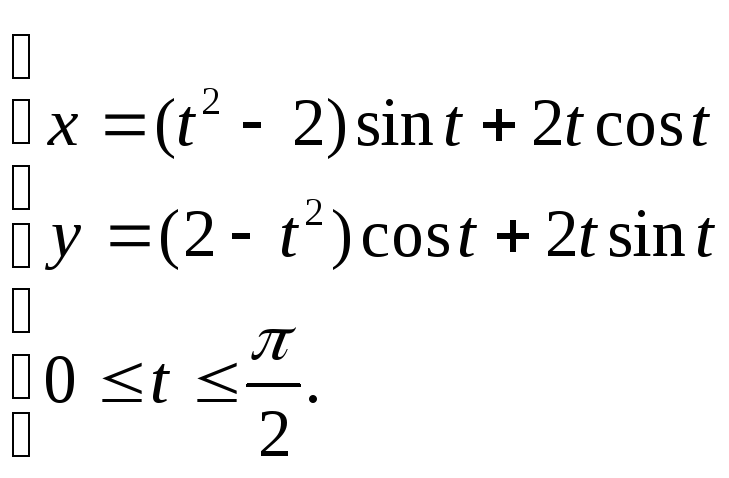
17.
 18.
18.

19.
 20.
20.

21.
 22.
22.

23.
 24.
24.

25.
 26.
26.

27.
 28.
28.

29.
 30.
30.

V. Вычислить несобственный интеграл или установить его расходимость
1.![]() .
2.
.
2.
![]() 3.
3.
![]() .
4.
.
4.
 5.
5.
![]() .
.
6. .
7.
.
7.![]() 8.
8.![]() 9.
9.
![]() 10.
10.
![]() .
.
11.![]() .
12.
.
12.
![]() .
13.
.
13.
![]() .
14.
.
14.![]() .
15.
.
15.
![]() .
.
16.![]() .
17.
.
17.![]() .
18.
.
18.![]() .
19.
.
19. .
20.
.
20. .
.
21.![]() .
22.
.
22. .
23.
.
23.![]() .
24.
.
24.![]() .
25.
.
25.![]() .
.
26.
![]() .
27.
.
27.![]() .
28.
.
28.![]() .
29.
.
29.![]() .
30.
.
30.![]() .
.
VI. Вычислить двойные интегралы:
1.

2.

3.

4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.

10.
![]()
11.
![]()
12.

13.

14.
![]()
15. Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]()
16.
Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]()
17.
Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]() .
.
18.
Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]() .
.
19.
Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]() .
.
20.
Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]()
21.
Вычислить
![]() ,
если областьD
удовлетворяет неравенствам:
,
если областьD
удовлетворяет неравенствам:
![]()
![]() .
.
22.
Вычислить
![]() ,
если область D
задана неравенствами:
,
если область D
задана неравенствами:
![]() .
.
23.
Вычислить
![]() ,
если D:
,
если D:![]() .
.
24.
Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]() .
.
25.Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]()
26.
Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]()
27.
Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]()
28.
Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]()
29.
Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]()
30.
Вычислить
![]() ,
если D
ограничена линиями:
,
если D
ограничена линиями:
![]()
VII. Вычислить криволинейные интегралы:
1. Вычислить
криволинейный интеграл![]() ,
где l
- дуга кривой у = х 2
от точки
А до В, где А (-3;9) до В (-1;1).
,
где l
- дуга кривой у = х 2
от точки
А до В, где А (-3;9) до В (-1;1).
2. Вычислить
криволинейный интеграл![]() ,
где l
- отрезок АВ, где А (1;1) до В (3;4).
,
где l
- отрезок АВ, где А (1;1) до В (3;4).
3. Вычислить по
формуле Грина:![]() ,
где С:
х 2
+ у 2 =
4.
,
где С:
х 2
+ у 2 =
4.
4. Вычислить
![]() ,
где А (0;0), В (π;2π), т.е. линия интегрирования
отрезок АВ от А к В.
,
где А (0;0), В (π;2π), т.е. линия интегрирования
отрезок АВ от А к В.
5. Вычислить по
формуле Грина:![]() ,
где С:
у = х; х = 2; у = 0.
,
где С:
у = х; х = 2; у = 0.
6. Вычислить по
формуле Грина:![]() ,
где С:
х 2
+ у 2 =
16.
,
где С:
х 2
+ у 2 =
16.
7. Вычислить
8. Вычислить по
формуле Грина:![]() ,
где С:
х 2
+ у 2 =
36.
,
где С:
х 2
+ у 2 =
36.
9. Вычислить по
формуле Грина:![]() ,
где С:
х 2
+ z
2 =
16.
,
где С:
х 2
+ z
2 =
16.
10. Вычислить
криволинейный интеграл![]() ,
где l
-отрезок прямой х = t
+1, y
= 2t
+1, z
= 3t
+1 от точки А (1;1;1) до В (2;3;4).
,
где l
-отрезок прямой х = t
+1, y
= 2t
+1, z
= 3t
+1 от точки А (1;1;1) до В (2;3;4).
11. Вычислить
криволинейный интеграл![]() ,
где l
-отрезок прямой y
= kx
от точки А (0;0) до В (2;6).
,
где l
-отрезок прямой y
= kx
от точки А (0;0) до В (2;6).
12. Вычислить
криволинейный интеграл![]() вдоль линии у = ln
x
от точки А (1;0) до В (е;1).
вдоль линии у = ln
x
от точки А (1;0) до В (е;1).
13. Вычислить
криволинейный интеграл![]() вдоль линии у = x
при 0≤х≤2
вдоль линии у = x
при 0≤х≤2
14. Вычислить
криволинейный интеграл:![]() ,
где С –
прямоугольник,
образованный прямыми: х
= 0, х = 1, у =
0, у = 2.
,
где С –
прямоугольник,
образованный прямыми: х
= 0, х = 1, у =
0, у = 2.
15. Вычислить
криволинейный интеграл
 .
.
16. Вычислить
криволинейный интеграл![]() , где L
– дуга параболы х = у 2
от точки А
(1;1) до В (25;5).
, где L
– дуга параболы х = у 2
от точки А
(1;1) до В (25;5).
17. Вычислить
криволинейный интеграл![]() , где L
– дуга кривой у = х 2
от точки А
(1;1) до В (2;4).
, где L
– дуга кривой у = х 2
от точки А
(1;1) до В (2;4).
18. Вычислить
криволинейный интеграл:![]() ,
где С – контур
треугольника, образованного осями
координат и прямой
,
где С – контур
треугольника, образованного осями
координат и прямой
![]() (обход против часовой стрелки).
(обход против часовой стрелки).
19. Вычислить
криволинейный интеграл![]() , где АВ – дуга кривой у = х 2
от точки А
(1;1) до В (2;4).
, где АВ – дуга кривой у = х 2
от точки А
(1;1) до В (2;4).
20. Вычислить
криволинейный интеграл![]() , где АВ – дуга кривой у = х 2
от точки А
(0;0) до В (1;1).
, где АВ – дуга кривой у = х 2
от точки А
(0;0) до В (1;1).
21. Вычислить
криволинейный интеграл
 .
.
22. Вычислить
криволинейный интеграл![]() ,
вдоль окружности х 2
+ у 2
=1 , обходя ее против хода часовой стрелки.
,
вдоль окружности х 2
+ у 2
=1 , обходя ее против хода часовой стрелки.
23. Вычислить
криволинейный интеграл![]() , где АВ – дуга кривой у = х 2
от точки А
(-1;1) до В (1;1).
, где АВ – дуга кривой у = х 2
от точки А
(-1;1) до В (1;1).
24. Вычислить
криволинейный интеграл![]() вдоль линии у = 2 x
при 0≤х≤2
вдоль линии у = 2 x
при 0≤х≤2
25. Вычислить
криволинейный интеграл![]() вдоль линии у = x
при 0≤х≤1
вдоль линии у = x
при 0≤х≤1
26. Вычислить
криволинейный интеграл![]() вдоль линии у = x
при 0≤х≤1
вдоль линии у = x
при 0≤х≤1
27. Вычислить
криволинейный интеграл![]() вдоль линии у = 2x
при 0≤х≤1
вдоль линии у = 2x
при 0≤х≤1
28. Вычислить
криволинейный интеграл![]() вдоль линии у = 4x
при 0≤х≤2
вдоль линии у = 4x
при 0≤х≤2
29. Вычислить
криволинейный интеграл![]() вдоль линии у = x2
при 0≤х≤1
вдоль линии у = x2
при 0≤х≤1
30. Вычислить
криволинейный интеграл![]() вдоль линии у = x
при 0≤х≤1
вдоль линии у = x
при 0≤х≤1
