
- •1. Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.
- •Закон сохранения заряда
- •Закон кулона
- •8. Поле равномерно заряженного бесконечного цилиндра (нити). Бесконечный цилиндр
- •11. Геометрическое место точек, имеющих одинаковые потенциалы, называют эквипотенциальной поверхностью
- •Второй закон Кирхгофа:
1. Электри́ческий заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.
Закон сохранения заряда
Электрический заряд замкнутой системы[5] сохраняется во времени и квантуется — изменяется порциями, кратными элементарному электрическому заряду, то есть, другими словами, алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе.
В рассматриваемой системе могут образовываться новые электрически заряженные частицы, например, электроны — вследствие явления ионизации атомов или молекул, ионы — за счёт явления электролитической диссоциации и др. Однако, если система электрически изолированна, то алгебраическая сумма зарядов всех частиц, в том числе и вновь появившихся в такой системе, всегда равна нулю.
Закон кулона
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме направлена вдоль прямой, соединяющей заряды, прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
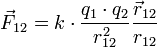
![]()
Относи́тельная диэлектри́ческая проница́емость среды ε — безразмерная физическая величина, характеризующая свойства изолирующей (диэлектрической) среды. Связана с эффектом поляризации диэлектриков под действием электрического поля (и с характеризующей этот эффект величиной диэлектрической восприимчивости среды). Величина ε показывает, во сколько раз сила взаимодействия двух электрических зарядов в среде меньше, чем в вакууме.
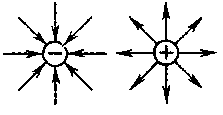
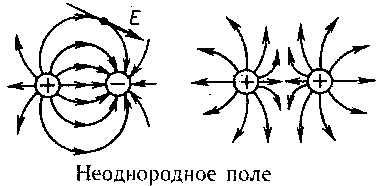
2. Электрическое поле – особый вид материи, через которое передается взаимодействие электрических зарядов. Оно возникает вокруг электрических зарядов.
Напряжённость электри́ческого по́ля —
векторная
физическая величина, характеризующая
электрическое
поле в данной точке и численно
равная отношению силы
![]() действующей
на неподвижный[1]
пробный
заряд, помещенный в данную точку
поля, к величине этого заряда
действующей
на неподвижный[1]
пробный
заряд, помещенный в данную точку
поля, к величине этого заряда
![]() :
:
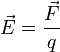 .
.
3. Если в данной точке пространства различные заряды создают электрические поля, напряженности которых E1, E2, E3, … , то результирующая напряженность поля в этой точке равна векторной сумме полей:
![]()
4.
Вектор электрической индукции, в сущности, представляет собой сумму двух совершенно различных физических величин: напряженности поля и ( умноженной на 4л) поляризации единицы объема среды. Тем не менее введение в рассмотрение этого вектора чрезвычайно упрощает изучение поля в диэлектриках. [3]
Итак, вектор электрической индукции представляет собой силу, действующую на точечный заряд в единицу положительного электричества, когда этот заряд помещен в бесконечно узком - зазоре, грани которого
D = 0E.
Поток линий
N = ES0cos α
5. теорема Остроградского—Гаусса: поток вектора напряженности через замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на произведение электрической постоянной и диэлектрической проницаемости среды.
![]()
В качестве поверхности площадью S
выберем цилиндрическую поверхность,
образующая которой перпендикулярна
плоскости. Основания этого цилиндра
расположены перпендикулярно линиям
напряженности по обе стороны от плоскости.
Так как образующие цилиндра параллельны
линиям напряженности (α = 90°, cos α
= 0), то поток через боковую поверхность
цилиндра отсутствует, и полный поток
через поверхность цилиндра равен сумме
потоков через два основания: N = 2ES.
Внутри цилиндра заключен заряд q =
σS, поэтому, согласно теореме
Остроградского-Гаусса,
![]() ,
где ε = 1 (для вакуума), откуда следует,
что напряженность поля равномерно
заряженной бесконечной плоскости
,
где ε = 1 (для вакуума), откуда следует,
что напряженность поля равномерно
заряженной бесконечной плоскости
![]()
6. Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +0. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией.
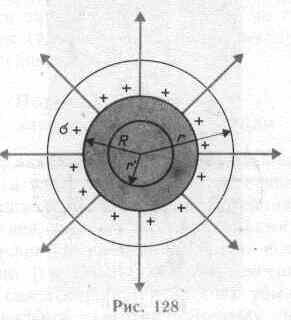
Поэтому линии напряженности направлены радиально (рис. 128). Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса (81.2), 4r2E=Q/0, откуда
![]()
При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. График зависимости E от r приведен на рис. 129. Если r'<R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E=0).
7. Шар
радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью (=dQ/dV— заряд, приходящийся на единицу объема). Учитывая соображения симметрии (см.п.3), можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае (см. (82.3)). Внутри же шара напряженность поля будет другая. Сфера радиуса r'<R охватывает заряд Q'=4/3r'3. Поэтому, согласно теореме Гаусса (81.2), 4r'2E=Q'/0=4/3r3/0. Учитывая, что =Q/(4/3R3), получим
![]()
Таким образом, напряженность ноля вне равномерно заряженного шара описывается формулой (82.3), а внутри его изменяется линейно с расстоянием r' согласно выражению (82.4). График зависимости E от r приведен на рис. 130.
