
шпоры часть 2
.docx|
Определенный интеграл. Формула Ньютона-Лейбница. |
|
|
|
Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю:
где
Формула Ньютона-Лейбница Пусть функция f (x) непрерывна на замкнутом интервале [a, b]. Если F (x) - первообразная функции f (x) на[a, b], то
Замена переменной в определенном интеграле Определенный
интеграл
Новые пределы интегрирования по переменной t определяются выражениями
где g -1 - обратная функция к g, т.е. t = g -1(x). Интегрирование по частям для определенного интеграла В этом случае формула интегрирования по частям имеет вид:
где |
Свойства определенного интеграла
Ниже предполагается, что f (x) и g (x) - непрерывные функции на замкнутом интервале [a, b].
-

-
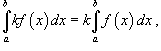 где k -
константа;
где k -
константа; -

-

-
Если
 для
всех
для
всех  ,
то
,
то  .
. -
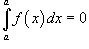
-
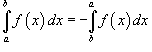
-
Если
 в
интервале [a,
b], то
в
интервале [a,
b], то 


 по
переменной x можно
преобразовать в определенный интеграл
относительно переменной t с
помощью подстановки x
= g (t):
по
переменной x можно
преобразовать в определенный интеграл
относительно переменной t с
помощью подстановки x
= g (t):