34.Величины, характеризующие напряженное состояние тела.

35.Напряжения, возникающие в теле под действием внешних сил.

В случае одноосного растяжения возникающие в теле напряжения равны. Сила Р (рис.3.1), приложенная к некоторой площадке F,обычно направле­на к ней под некоторым углом. Поэтому в теле возникают нормальные и касательные напряжения. Различают временные напряжения, обусловленные действием внешней нагрузки, которые исчезают после снятия нагрузки, и внутренние напряжения, возникающие и уравновешивающиеся в пределах те­ла.

Образование внутренних напряжений связано в основном с неоднород­ным распределением деформаций (в том числе и микродеформаций) по объ­ему тела.

Наличие в испытуемом образце механических надрезов, трещин внут­ренних дефектов металла приводит к неравномерному распределению напря­жений, создавая у основания надреза пиковую концентрацию нормальных напряжений (нормальные напряжения бывают растягивающими и сжимающи­ми)(рис.3.2). Действие надрезов, сделанных в образце, аналогично конфи­гурации изделий, имеющих сквозные отверстия, резьбу и т.п., или влия­нию внутренних дефектов металла (неметаллических включений, графитных выделений в чугуне, трещин и др.), нарушающих его цельность. Поэтому всевозможные надрезы, отверстия, галтели и другие источники концентра­ции напряжений называют концентраторами напряжений.

Напряжения вызываются различными причинами. Различают времен­ные, обусловленные действием внешней нагрузки и исчезающие после ее снятия ; внутренние остаточные напряжения, возникающие и уравновеши­вающиеся в пределах тела без действия внешней нагрузки. Внутренние нап­ряжения наиболее часто возникают в процессе быстрого нагрева или ох­лаждения металла вследствие неодинакового расширения (сжатия) поверх­ностных и внутренних слоев. Эти напряжения называют тепловыми. Кроме того, напряжения возникают в процессе кристаллизации, при неравномер­ной деформации, при термической обработке вследствие структурных прев­ращений по объему и т.д., эти напряжения называют фазовыми или струк­турными.

Внутренние напряжения классифицируют:

-напряжения 1 рода (или зональные),называемые также макронапряжени­ями, они уравновешиваются в объеме всего тела, возникают главным обра­зом в результате технологических процессов, которым подвергают деталь в процессе ее изготовления.

-напряжения 2 рода уравновешиваются в объеме зерна (кристаллита) или нескольких блоков (субзерен), их называют иначе микронапряжениями. Чаще всего они возникают в процессе фазовых превращений и деформации металла, когда разные кристаллиты и блоки внутри них оказываются в различном упругонапряженном состоянии.

-напряжения 3 рода, локализующиеся в объемах кристаллической ячей­ки, представляют собой статические искажения решетки, т. е. смещения атомов на доли ангстрема из узлов кристаллической решетки.

36.Главные нормальные и главные касательные напряжения.

См. 34 вопрос+

Через точку тела, находящегося в напряженном состоянии, можно провести бесконечное множество взаимно перпендикулярных плоскостей. И только на единственной тройке плоскостей будут отсутствовать касательные напряжения и действовать только нормальные. Такие площадки называются главными. Нормальные напряжения на этих площадках называются главными нормальными напряжениями и обозначаются , а оси, вдоль которых они действуют –главными осями. Напряженное состояние в точке вполне определяется направлением главных осей и величиной главных нормальных напряжений.

Различают 9 схем главных напряжений: 2 линейные (растяжение, сжатие), 3 плоские (р-р, с-с, р-с) и 4 объемные (р-р-р, с-с-с, р-с-с, р-р-с).

 

Если напряженное состояние точки задано главными напряжениями, то все формулы значительно упрощаются.

 

Полное напряжение: 

Нормальное напряжение: 

Касательные напряжения:

Проекции полного напряжения: ; ; .

Используя соотношение , получим. Это уравнение эллипсоида, отнесенное к центру и главным осям, называют эллипсоидом напряжений. Полуоси эллипсоида напряжений равны главным напряжениям. Любой отрезок от центра до пересечения с поверхностью представляет величину полного напряжения S на площадке, перпендикулярной отрезку. При равенстве двух главных напряжений эллипсоид превращается в эллипсоид вращения, а при равенстве трех главных напряжений – в шар.

Если из главных плоскостей построить куб, то внутри этого куба имеется 6 плоскостей, на которых действуют главные касательные напряжения. Эти плоскости проходят через диагонали куба.

Главные касательные напряжения (с учетом знака) определяются по формулам:

Графическое представление соотношения главных нормальных и главных касательных напряжений дают круги Мора.

 

На площадках, где действуют главные касательные напряжения, имеются и свои нормальные напряжения. Они определяются по следующим формулам:

Шесть плоскостей главных касательных напряжений образуют правильный двенадцатигранник – додекаэдр. Поэтому их иногда называют додекаэдрическими.

ОКТАЭДРИЧЕСКИЕ НАПРЯЖЕНИЯ

Наряду с площадками, по которым действуют главные нормальные и главные касательные напряжения, большое значение в теории пластической деформации имеют площадки, равнонаклоненные к главным осям, а значит отсекающие от них отрезки одинаковой длины. Эти площадки называются октаэдрическими. Всего их 8 и вместе они образуют правильный 8-гранник – октаэдр. Эти площадки попарно взаимно параллельны. Поэтому независимых всего 4. Напряжения, действующие на этих площадках, называются октаэдрическими.

 

 

Определим нормальное и касательное октаэдрические напряжения.

Поскольку площадки равнонаклонены к главным осям, . Тогда из равенстваимееми

Полное октаэдрическое напряжение определим по формуле , подставив туда значение направляющих косинусов:

.

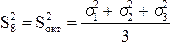Из выражения получим выражение для нормального октаэдрического напряжения:

Касательное октаэдрическое напряжение:

После всех преобразований получим выражение для интенсивности касательных напряжений в главных осях:

.

В произвольных напряжениях:

,

в главных касательных напряжениях:

.

По аналогии с интенсивностью касательных напряжений вводится понятие интенсивность нормальных напряжений:  ; 

 

Таким образом, через точку тела, находящегося в напряженном состоянии, можно провести 13 характерных площадок:

_- 3 главные площадки, на которых действуют только нормальные напряжения _;

- 6 площадок, на которых действуют главные касательные напряжения и нормальные_;

- 4 октаэдрические площадки, на которых действуют равные для всех площадок октаэдрические напряжения .

 

Если к этим 13-и площадкам добавить им параллельные, то получится 20-гранник.