8.6. Дисперсионный анализ для разложения общей суммы квадратов отклонений. Степени свободы для соответствующих сумм квадратов отклонений

Применим изложенную выше теорию для парной линейной регрессии.

После того, как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.

Оценка значимости уравнения регрессии в целом даётся с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т.е. b = 0, и, следовательно, фактор х не оказывает влияния на результат у.

Непосредственному расчёту F-критерия предшествует анализ дисперсии. Центральное место в нём занимает разложение общей суммы квадратов отклонений переменной у от среднего значения на две части – “объяснённую” и “необъяснённую”:

(8.21)

Общая сумма квадратов отклонений =

Сумма квадратов отклонений, объяснённая дисперсией

Остаточная сумма квадратов отклонений

Здесь

Уравнение (8.21) является следствием системы нормальных уравнений, выведенных в одной предыдущих тем.

Доказательство выражения (8.21).

Осталось доказать, что последнее слагаемое равно нулю.

Если сложить от 1 до n все уравнения

y_i = a+bx_i+e_i, (8.22)

то получим y_i = a1+bx_i+e_i. Так как e_i =0 и 1 =n, то получим

. (8.23)

Тогда .

Если же вычесть из выражения (8.22) уравнение (8.23), то получим

. (8.24)

Или

, (8.25)

В результате получим

.

Последние суммы равны нулю в силу системы двух нормальных уравнений.

Общая сумма квадратов отклонений индивидуальных значений результативного признака у от среднего значения вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы. Если фактор на оказывает никакого влияния на результат, то линия регрессии параллельна осиOX и . Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связана с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объяснённая регрессией, совпадает с общей суммой квадратов.

Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный влиянием фактора х, т.е. регрессией у по х, так и вызванный действием прочих причин (необъяснённая вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объяснённую вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное влияние на признак у. Это равносильно тому, что коэффициент детерминации будет приближаться к единице.

Любая сумма квадратов связана с числом степеней свободы (df – degrees of freedom), с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n и с числом определяемых по ней констант. Применительно к исследуемой проблеме число степеней свободы должно показать, сколько независимых отклонений из n возможных [] требуется для образования данной суммы квадратов. Так, для общей суммы квадратовтребуется (n-1) независимых отклонений, ибо по совокупности из n единиц после расчёта среднего свободно варьируют лишь (n-1) число отклонений. Например, мы имеем ряд значений у: 1,2,3,4,5. Среднее из них равно 3, и тогда n отклонений от среднего составят: -2, -1, 0, 1, 2. Так как, то свободно варьируют лишь четыре отклонения, а пятое отклонение может быть определено, если предыдущие четыре известны.

При расчёте объяснённой или факторной суммы квадратов используются теоретические (расчётные) значения результативного признака

Тогда сумма квадратов отклонений, обусловленных линейной регрессии, равна

.(8.26)

Поскольку при заданном объёме наблюдений по x и y факторная сумма квадратов при линейной регрессии зависит только от константы регрессии b, то данная сумма квадратов имеет только одну степень свободы.

Существует равенство между числом степеней свободы общей, факторной и остаточной суммой квадратов отклонений. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет n-2. Число степеней свободы общей суммы квадратов определяется числом единиц варьируемых признаков, и поскольку мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы, т.е. df_общ. = n–1.

Итак, имеем два равенства:

, (8.27)

n-1 = 1 + (n-2)

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D.

;

;

.

Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчёте на одну степень свободы, получим величину F-критерия Фишера

,

где F-критерий для проверки нулевой гипотезы H₀: D_факт = D_ост.

Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для H₀ необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при различных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признаётся достоверным, если оно больше табличного. Если F_факт > F_табл, то нулевая гипотеза H₀: D_факт = D_ост об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи.

Если F_факт < F_табл, то вероятность нулевой гипотезы H₀: D_факт = D_ост выше заданного уровня (например, 0,05) и она не может быть отклонена без серьёзного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Гипотеза H₀ не отклоняется.

В рассматриваемом примере из главы 3:

= 131200 -7*144002 = 30400 – общая сумма квадратов;

= =1057,878*(135,43-7*(3,92571)²) = 28979,8 – факторная сумма квадратов;

=30400-28979,8 = 1420,197 – остаточная сумма квадратов;

D_факт = 28979,8;

D_ост = 1420,197/(n-2) = 284,0394;

F_факт =28979,8/284,0394 = 102,0274;

F_{=0,05; 2; 5} =6,61; F_{=0,01; 2; 5} = 16,26.

Поскольку F_факт > F_табл как при 1%-ном, так и при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).

Величина F-критерия связана с коэффициентом детерминации . Факторную сумму квадратов отклонений можно представить как

,

а остаточную сумму квадратов – как

.

Тогда значение F-критерия можно выразить как

.

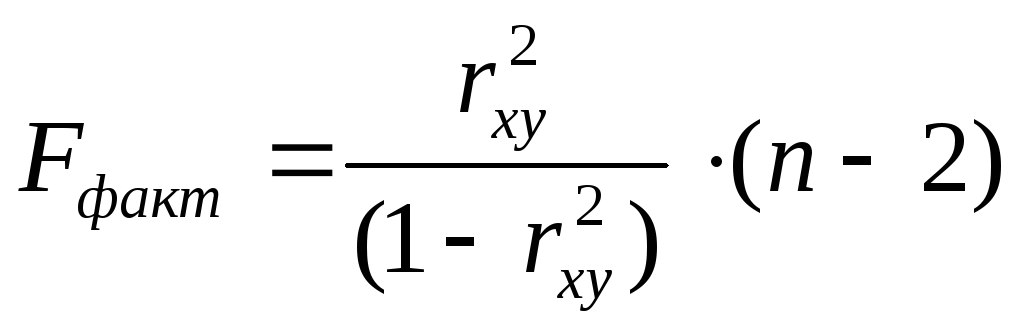Оценка значимости регрессии обычно даётся в виде таблицы дисперсионного анализа

Источники вариации	Число степеней свободы	Сумма квадратов отклонений	Дисперсия на одну степень свободы	F-отношение
				фактическое	Табличное при =0,05
Общая	6	30400
Объяснённая	1	28979,8	28979,8	102,0274	6,61
Остаточная	5	1420,197	284,0394

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из его параметров определяется его стандартная ошибка: m_b и m_a.

Стандартная ошибка m_b коэффициента регрессии b, как было выведено ранее, определяется по формуле

где - остаточная дисперсия D_ост на одну степень свободы.

Для нашего примера

Стандартная ошибка коэффициента регрессии a определяется по формуле

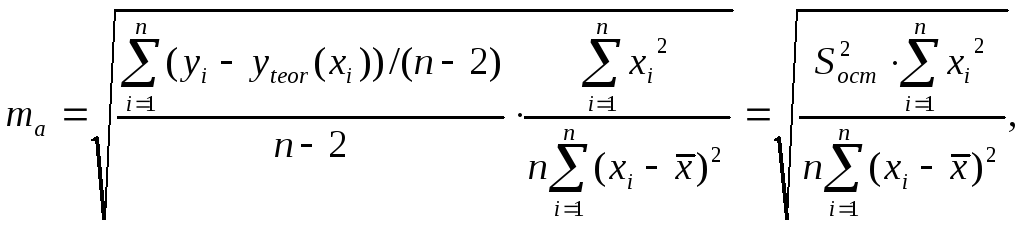
где – остаточная дисперсия D_ост на одну степень свободы.

Процедура оценивания существенности данного параметра а такая же, как и для параметра b: вычисляется t-критерий , его величина сравнивается с табличным значением при определённом уровне значимости α и числе степеней свободы (n-2).