8.3. Доверительные интервалы для зависимой переменной

Одной из центральных задач эконометрического моделирования является предсказание (прогнозирование) значений зависимой переменной при определенных значениях объясняющих переменных. Здесь возможен двоякий подход: либо предсказать условное математическое ожидание зависимой переменной при определенных значениях объясняющих переменных (предсказание среднего значения), либо прогнозировать некоторое конкретное значение зависимой переменной (предсказание конкретного значения).

Предсказание среднего значения. Пусть построено уравнение парной регрессии y_teor(x_i) = b₀ + b₁x_i, на основе которого необходимо предсказать условное математическое ожидание М(YХ = х_p) переменной y_teor(x_p) при X = х_p. В данном случае значение y_teor(x_p) = b₀ + b₁x_p является оценкой (приближением) М(YХ = х_p). Тогда естественным является вопрос, как сильно может уклониться модельное среднее значение y_teor(x_p), рассчитанное по эмпирическому уравнению регрессии, от соответствующего истинного условного математического ожидания y_teor,true(x_p) = ₀ + ₁x_p. Ответ на этот вопрос дается на основе интервальных оценок, построенных с заданной надежностью (1-) при любом конкретном значении х_р объясняющей переменной.

Чтобы построить доверительный интервал, покажем, что случайная величина y_teor(x_p) имеет нормальное распределение с конкретными параметрами. Используя формулы (8.1), (8.2), имеем:

y_teor(x_p) = b₀ + b₁x_p = d_i y_i +( c_i y_i)x_p = (d_i +c_ix_p)y_i.

Следовательно, y_teor(x_p) является линейной комбинацией нормальных случайных величин и, значит, сама имеет нормальное распределение.

My_teor(x_p) = M(b₀ + b₁x_p) = M(b₀)+ M(b₁)x_p = ₀ + ₁x_p ,

Dy_teor(x_p) = D(b₀ + b₁x_p) = D(b₀)+ D(b₁) +2cov(b₀ ,b₁)x_p, (8.12)

(здесь используются формулы: D(X+Y) = D(Х)+D(У)+ 2соv(Х, Y); D(сХ) = с²D(Х); cov(Х, bY) = bсоv(Х, Y)).

cov(b₀ ,b₁) = M[(b₀ – M(b₀)(b₁ – M(b₁))] =

= M[(b₀ - ₀)(b₁ – ₁)] = M[((b₁ – M(b₁))] =

= - M[(b₁ - M(b₁)(b₁ – M(b₁))] =  M[(b₁ - ₁)(b₁ – ₁)] =

= -D(b₁) = .

Следовательно,

==

=.(8.13)

Так как

,

Поскольку

Подставив вместо ² её несмещенную оценку получим выборочную исправленную дисперсию D(y_teor(x_p)) рассматриваемой случайной величины. Тогда случайная величина

(8.14)

имеет распределение Стьюдента с числом степеней свободы  = n–2. Следовательно, по таблице критических точек распределения Стьюдента по требуемому уровню значимости  и числу степеней свободы =n–2 можно определить критическую точку t_/2,n-2, удовлетворяющую условию Р(Т < t_/2,n-2) = 1–.

С учетом (7.3) имеем:

(8.15)

После алгебраических преобразований получим:

=1-. (8.16)

Таким образом, доверительный интервал для гипотезы H₀: M(YX=x_p) = ₀ + _0*х_р имеет вид:

;

. (8.17)

В верхней строке приведена нижняя граница доверительного интервала, в нижней строке – верхняя граница доверительного интервала, в котором с надёжностью 1– находятся значения зависимого фактора, лежащие на линии регрессии

Для проверки гипотезы

H₀: M(YX=x_p) = y_p;

H₁: M(YX=x_p)  y_p;

используется статистика:

(8.18)

имеющая распределение Стьюдента с числом степеней свободы  = n -2. Поэтому H₀ отклоняется, если |T_набл |  t_/2,n-2 (– требуемый уровень значимости).

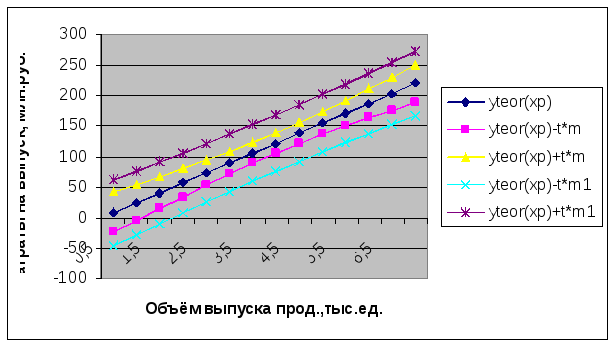Рис. 8.1. Диаграмма нижних и верхних доверительных границ для индивидуальных значений и значений, лежащих на линии регрессии, а также самой линии регрессии

Поскольку фактические индивидуальные значения зависимой переменной Y варьируют около среднего регрессионного значения y_teor(x_p) = b₀ + b₁x_p, и так как они могут отклоняться от y_teor(x_p) = b₀ + b₁x_p на величину среднеквадратического отклонения ², которая оценивается как корень квадратный из дисперсии , то нижние и верхние границы оцениваются соответственно следующим образом:

;

.