ния равноточные, можно считать, что все эти дисперсии равны между собой (предпосылка 2⁰) D(_i) = _² = .

Приведем формулы связи дисперсий коэффициентов D(b₀) и D(b₁) с дисперсией ² случайных отклонений _i. Для этого представим формулы определения коэффициентов b₀ и b₁ в виде линейных функций относительно значений Y:

.

Отсюда

,

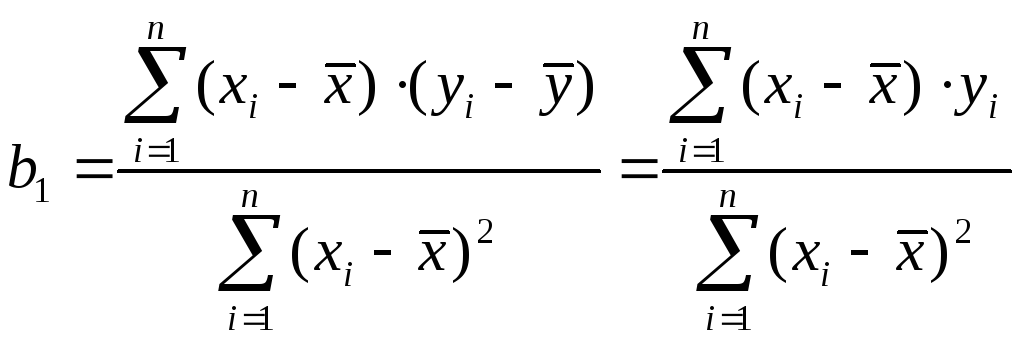так как .

Введя обозначение

,

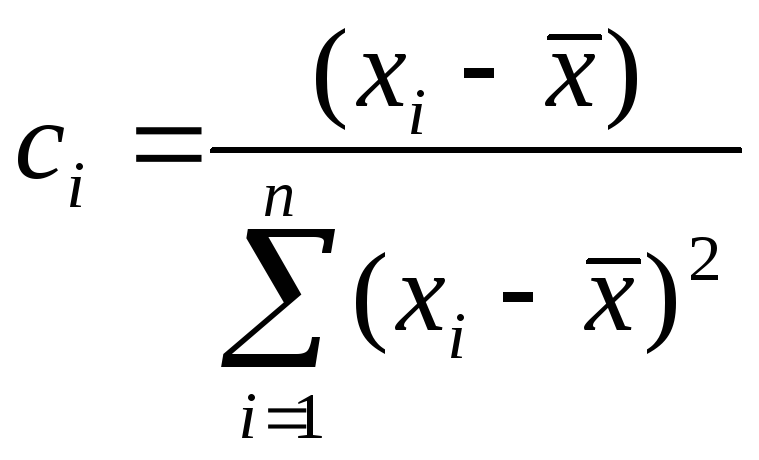имеем:

. (8.1)

Аналогично:

.

Обозначив

,

имеем:

. (8.2)

Так как предполагается, что дисперсия Y постоянна и не зависит от значений X, то с_i и d_i можно рассматривать как некоторые постоянные. Следовательно,

, (8.3)

и,

.

Таким образом,

D(b₀)= . (8.4)

Из соотношений (8.3), (8.4) очевидны следующие выводы.

• Дисперсии b₀ и b₁ прямо пропорциональны дисперсии случайного отклонения ² зависимой переменной Y. Следовательно, чем больше фактор случайности по переменной Y, тем менее точными будут оценки.

• Чем больше число n наблюдений, тем меньше дисперсии оценок. Это вполне логично, так как чем большим числом данных мы располагаем, тем вероятнее получение более точных оценок.

• Чем больше дисперсия (разброс значений ) объясняющей переменной X, тем меньше дисперсия оценок коэффициентов. Другими словами, чем шире область изменений объясняющей переменной, тем точнее будут оценки (тем меньше доля случайности в их определении).

В силу того, что случайные отклонения _i по выборке определены быть не могут, при анализе надежности оценок коэффициентов регрессии они заменяются отклонениями e_i = y_i – b₀ – b₁x_i значений y_i переменной Y от оцененной линии регрессии. Дисперсия случайных отклонений D(_i) = ² заменяется ее несмещенной оценкой

. (8.5)

Тогда

, (8.6)

. (8.7)

Здесь – необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии). Отметим, что корень квадратный из необъясненной дисперсии, т.е. , называется стандартной ошибкой оценки (стандартной ошибкой регрессии).

и – стандартные отклонения случайных величин b₀ и b₁, называемые стандартными ошибками коэффициентов регрессии (иногда они обозначаются m_b0 и m_b1 соответственно или стандартными ошибками). Надо отметить, что их значения вычисляются автоматически при построении регрессии первым и вторым способами.

8.2. Проверка гипотез о значимости коэффициентов линейного уравнения регрессии

Эмпирическое уравнение регрессии определяется на основе конечного числа статистических данных. Поэтому коэффициенты эмпирического уравнения регрессии являются случайными величинами, изменяющимися от выборки к выборке. При проведении статистического анализа перед исследователем зачастую возникает необходимость сравнения эмпирических коэффициентов регрессии b₀ и b₁ с некоторыми теоретически ожидаемыми (истинными по генеральной совокупности) значениями ₀ и ₁ этих коэффициентов. Данный анализ осуществляется по схеме статистической проверки гипотез, которая подробно проанализирована в пунктах 2.3–2.4.

Для проверки гипотезы

Н₀: b₁ = ₁,

H₁: b₁ ≠ ₁

используется статистика

, (8.8)

которая при справедливости гипотезы Н₀ имеет распределение Стьюдента с числом степеней свободы  = n–2, где n – объем выборки. Следовательно, Н₀: b₁ = ₁ отклоняется на основании данного критерия, если

, (8.9)

где  — требуемый уровень значимости. При невыполнении (8.9) считается, что нет оснований для отклонения H₀.

Наиболее важной на начальном этапе статистического анализа построенной модели все же является задача установления наличия линейной зависимости между Y и X. Эта проблема может быть решена по той же схеме:

Н₀: b₁ = 0,

H₁: b₁ ≠ 0.

Гипотеза в такой постановке обычно называется гипотезой о статистической значимости коэффициента регрессии. При этом, если Н₀ принимается, то есть основания считать, что величина Y не зависит от X. В этом случае говорят, что коэффициент b₁ статистически незначим (он слишком близок к нулю). При отклонении Н₀ коэффициент b₁ считается статистически значимым, что указывает на наличие определенной линейной зависимости между Y и X. В данном случае рассматривается двусторонняя критическая область, так как важным является именно отличие от нуля коэффициента регрессии, и он может быть как положительным, так и отрицательным.

Поскольку полагается, что ₁ = 0, то формально значимость оцененного коэффициента регрессии b₁ проверяется с помощью анализа отношения его величины к его стандартной ошибке . При выполнении исходных предпосылок модели эта дробь имеет распределение Стьюдента с числом степеней свободы = n-2, где n – число наблюдений. Данное отношение называется t–статистикой:

. (8.10)

Для t-статистики проверяется нулевая гипотеза о равенстве ее нулю. Очевидно, t = 0 равнозначно b₁ = 0, поскольку t пропорциональна b₁. Фактически это свидетельствует об отсутствии линейной связи между X и У.

По аналогичной схеме на основе t-статистики проверяется гипотеза о статистической значимости коэффициента b₀:

(8.11)

Отметим, что для парной регрессии более важным является анализ статистической значимости коэффициента b₁, так как именно в нем скрыто влияние объясняющей переменной X на зависимую переменную Y. Рассмотрим все сказанное выше на примере из главы 3.

Пример 3.1. Пусть имеются статистические данные об объёме выпуска некоторой продукции (X, тыс. единиц) и соответствующих затратах на производство (Y, млн. руб.). Требуется построить линейную регрессионную зависимость затрат от объёма выпуска.

i - номер измерения	Объём выпуска продукции, Xi, тыс. ед.	Затраты на выпуск продукции, Yi, млн руб.	Затраты на выпуск прод. теор, Yteor(xi), млн руб.	ei^2=(Yi–Yteor(xi))^2	xi^2
1	1	30	24,7481	27,582216	1
2	1,5	40	41,0106	1,0213898	2,25
3	3	100	89,7981	104,07702	9
4	4,5	120	138,585	345,42944	20,25
5	5,2	150	161,353	128,89638	27,04
6	5,8	170	180,868	118,11935	33,64
7	6,5	230	203,635	695,07132	42,25
xcp.=	3,92857	120		1420,1971	135,43
				(xi^2)cp.=	19,3471
			(xi^2)cp.-(xcp.)^2=		3,91346

10,36857.

3,220027.

10,10087.

Критическое значение при уровне значимости  = 0,05 равно 2,571.

Сравним модуль наблюдаемого значения = 10,10086 с критическим значениемt_0,025;5=2,571. Поскольку =10,10086> 2,571 =t_кр, то нулевая гипотеза {t = 0} должна быть отвергнута в пользу альтернативной при выбранном уровне значимости. Это подтверждает статистическую значимость коэффициента регрессии b₁.

Аналогично проверяется статистическая значимость коэффициента b₀:

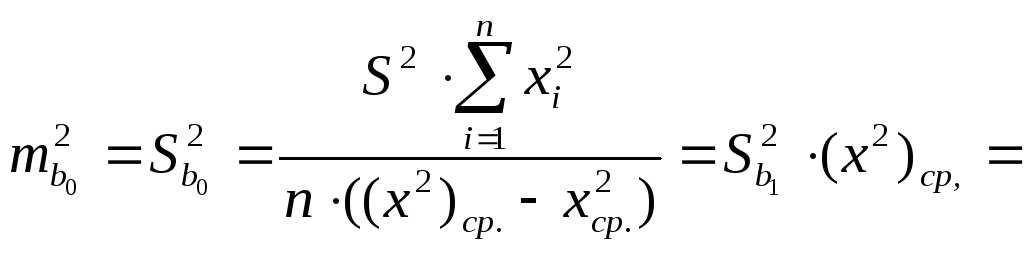10,3685619,3471 =

= 200,6021.

14,16341.

-0,54908.

Так как = 0,54908 < 2,571 =t_кр, то гипотеза о статистической незначимости коэффициента b₀ не отклоняется. Это означает, что в данном случае свободным членом уравнения можно пренебречь в смысле значимости.

При оценке значимости коэффициента линейной регрессии на начальном этапе можно использовать следующее «грубое» правило, позволяющее не прибегать к таблицам.

Если стандартная ошибка коэффициента больше его модуля (t 1), то коэффициент не может быть признан значимым, так как доверительная вероятность при двусторонней альтернативной гипотезе составит менее чем 0,7.

Если 1 <t 2, то найденная оценка может рассматриваться как относительно (слабо) значимая. Доверительная вероятность в этом случае лежит между значениями 0,7 и 0,97.

Если 2 <t 3 то это свидетельствует о значимой линейной связи между X и Y. В этом случае доверительная вероятность колеблется от 0,95 до 0,99.

Наконец, если t> 3, то это почти гарантия наличия линейной связи.

Конечно, в каждом конкретном случае имеет значение число наблюдений. Чем их больше, тем надежнее при прочих равных условиях выводы о значимости коэффициента. Однако для n>10 предложенное «грубое» правило практически всегда работает [3].