Формулы симметрии и тридцать два вида симметрии кристаллов

Перечень всех элементов симметрии кристалла, записанный в виде их символов, на­зывается формулой симметрии. Например, если в кристалле имеются три оси 1,2, три плоскости симметрии и центр симметрии (рис. 25, а), то его формулой симметрии будет З-С^ЗРС. Если кристалл обладает одной осью симметрии третьего порядка Ьз,тремя вертикальными и одной горизонтальной плоскостью симметрии и тремя осями второго порядка (рис. 25, б), то его формула симметрии будет ЬъЪЬъ^Р. Но одновременно в этом кристалле ось Ьз является осью 1^6. Поэтому его формулу симметрии можно записать и так: Х,-631/24Р. В таких формулах порядок записи следующий: сначала главные оси, затем другие, потом плоскости и центр инверсии.

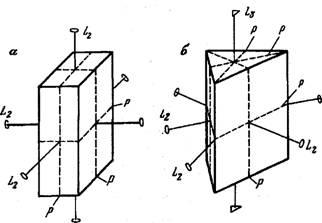
Рис. 25. Многогранники с разными наборами элементов симметрии.

Кристаллы одного и того же минерала независимо от их огранки характеризуются одно и той же формулой симметрии. Число таких формул не беспредельно, поскольку элементы симметрии взаимосвязаны между собой. Геометрический вывод всех воз­можных сочетаний элементов симметрии в кристаллах был сделан немецким минера­логом И. Гесселем в 1830 г. и финном А. В. Гадолиным в 1867 г. Из него следует, что в природе может существовать только 32 сочетания, или, как принято говорить, 32 вида симметрии, которые объединены в семь групп — семь сингоний. Перечень видов симметрии и сингоний приведен в табл. 5.

Сингонию кристалла определяют по обязательному для каждой сингоний элементу симметрии. В кристаллах кубической сингоний обязательно присутствуют четыре оси третьего порядка (41>з), в гексагональной сингоний — одна ось Ьв, тетрагональной — 1-4, тригональной — 1-з.СингоНии объединены в три категории—низшую, среднюю и высшую. В таблице указаны также принятые в кристаллографии названия видов сим­метрии— примитивный, планальный (плана-плоскость), аксиальный (акси-ось) и т.п.

Простыв кристаллографические формы

Естественные форма и огранка кристаллов зависят от их структуры и условий обра­зования. Каждая грань отвечает плоской сетке, а внешняя симметрия кристаллов соответствует симметрии их структуры.

Наиболее совершенные по своей огранке кристаллы образуются при равномерной диффузии вещества ко всем частям растущего кристалла и при одинаковой дефект­ности кристаллической решетки во всех ее частях. На таких кристаллах закономерно повторяются одинаковые грани. На одних кристаллах это грани только одного вида, например грани гексаэдра (куба), на других повторяются грани двух, трех и более видов. На кристаллах одинаковые грани соответствуют одинаковым плоским сеткам в структуре минерала, они характеризуются одним и тем же узором расположения атомов и схожим механизмом роста (рис. 26).

Рис. 26. Одинаковые узор и плотность рас­положения атомов на одинаковых гранях кри­сталла (Вадило, 1964).

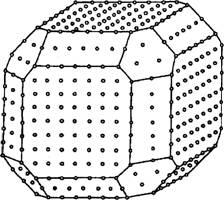
Совокупность граней кристалла, отвечающих одинаковым плоским сеткам, называ­ется простой кристаллографической формой. На кристалле, изображенном на рис. 26, имеется 26 граней, они принадлежат к трем простым кристаллографическим фор­мам. К одной простой форме относятся шесть граней, к другой — восемь, к третьей— двенадцать. Выделение простых кристаллографических форм на кристаллах имеет большой физический смысл, а именно: одинаковые грани характеризуются одними и теми же скоростями роста, блеском, твердостью и сходством других свойств.

На идеально развитом кристалле все грани одной и той же простой кристаллогра­фической формы одинаковы. Отсюда—сколько на равномерно развитом кристалле сортов граней, столько на нем и простых кристаллографических форм. Исходя из строгого определения, простой кристаллографической формой можно назвать сово­купность граней, связанных друг с другом элементами симметрии.

Чаще всего кристаллы огранены комбинацией нескольких простых кристаллогра­фических форм. Чтобы представить себе в объеме геометрические очертания каждой из них, надо мысленно продлить все грани данной простой кристаллографической формы так, как будто бы им не мешали расти грани других простых кристаллогра­фических форм, и попытаться оценить вид получившегося многогранника. Легко до­гадаться, что большие грани квадратных очертаний (их шесть) на рис. 26 есть грани гексаэдра (куба). Труднее представить, чем являются небольшие грани шестиуголь­ных очертаний. Их восемь, а если их сомкнуть друг с другом, получится многогранник из восьми равносторонних треугольников. Такой восьмигранник называется в геоме­трии октаэдром. Наконец, если мысленно соединить длинные прямоугольные грани, а их двенадцать, получится фигура, называемая ромбододекаэдром. Следовательно, можно сказать, что кристалл образован гранями трех простых кристаллографических форм — куба, октаэдра и ромбододекаэдра.

Доказано, что в мире кристаллов число простых кристаллографических форм огра­ничено. Всего их 47.

В сингониях низшей категории возможны моноэдры, диэдры, пинакоиды (от греч. monos—один; hedra (эдр) — сторона, грань; pinax—доска), ромбические призмы, ром­бические пирамиды, ромбические дипирамиды и ромбические тетраэдры (рис. 27).

Рис. 27. Простые формы низшей категории сингоний. В сингониях средней категории вероятны моноэдры, пинакоиды, призмы разного рода, различные пирамиды и дипирамиды, трапецоэдры, ромбоэдры, скаленоэдры, тетрагональные тетраэдры (рис. 28).

Рис. 28. Простые формы средней категории сингоний.

В кубической сингонии возможны 15 простых кристаллографических форм, из них на кристаллах минералов чаще всего наблюдаются тетраэдр, октаэдр, гексаэдр (куб), ромбододекаэдр, Пентагон-додекаэдр, тетрагон-триоктаэдр (рис. 29).

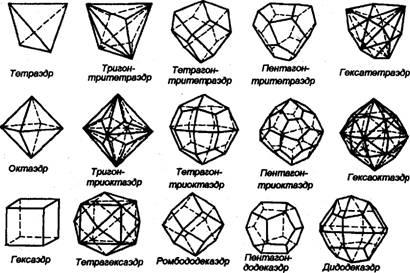
Рис. 29. Простые формы кубической сингонии.

Как видно, простые формы могут быть закрытыми и открытыми. Первые обра­зуют привычные всем геометрические фигуры, целиком ограничивающие какой-либо конечный объем. Таковы, например, куб, октаэдр, ромбоэдр, скаленоэдр, дипира-миды. Открытые формы являются незамкнутыми и тем самым они поначалу менее понятны. Таковы пирамиды с бесконечно расходящимися от вершины гранями, пина-коид (две беспредельно протяженные в пространстве параллельные друг другу плос­кости) и призмы, напоминающие беспредельно идущие трубы многоугольного сечения, ничем не ограниченные по их длине. Реальное сочетание в природе граней открытых и закрытых простых кристаллографических форм дает кристаллу его конечный те­лесный объем.