
- •Федеральное агенство железнодорожного
- •Введение
- •1.Общие положения
- •2. Прогнозирование материального потока
- •1. Метод наивного прогноза.
- •2. Метод простого среднего.
- •3. Метод скользящего среднего.
- •4. Метод регрессивного анализа.
- •3.Определение оптимального размера партии поставки.
- •4.Определение стоимости доставки продукции различными видами транспорта.
- •5. Определение потребного количества транспортных единиц
- •6.Определение основных параметров склада
4. Метод регрессивного анализа.
Прогнозируемое значение материального потока рассчитывается как значение математической функции, наиболее точно описывающей изменение значений материального потока за несколько предыдущих периодов.
В общем виде уравнение искомой функции может быть записано следующим образом:
N(t)=F(t)±δ (2.11)
где F(t)- значение функции в t-й год;
δ- погрешность, показывающая величину отклонения теоретических значений от экспериментальных.
Функция может иметь любой вид: прямая, парабола и т.д. Выбор функции, наиболее точно описывающей заданные изменения материального потока, осуществляются на основании минимизации значения погрешности δ, которое рассчитывается по формуле:
δ =
 (2.12)
(2.12)
где Nt – значение материального потока в t-й год (фактическое);
n – число наблюдений;
p – число параметров в уравнении тренда (число неизвестных).
Для анализа принимаем две функции: линейную и полином 2-го порядка:
f(t)= a+bt (2.13)
f1(t)= a+bt+ct2 (2.14)
где a – начальный уровень тренда;
b – средний абсолютный прирост в единицу времени, константа линейного тренда;
c- квадратичный параметр равный половине ускорения, константа параболического тренда.
Значение коэффициента a, b, c определены с помощью метода наименьших квадратов.
Продифференцируем каждое уравнение и составим систему нормальных уравнений:
* для линейного тренда:
 (2.15)
(2.15)
* для параболического тренда:
 (2.16)
(2.16)
Для упрощения
расчетов используем метод отсчета
времени от условного начала. Обозначим
в ряду изменения значений времени (t)
таким образом, чтобы
 стала равна нулю.
стала равна нулю.
Представим метод расчета и его результаты в виде таблицы:
Таблица 2.3
Расчет параметров тренда
|
№ |
|
N(
|
|
|
|
N( |
N( |
f( |
(f( |
|
( |
|
1 |
2 |
53,7 |
4 |
-8 |
16 |
-107,4 |
214,8 |
56,64 |
8,6436 |
58,68 |
24,8004 |
|
2 |
1 |
64 |
1 |
1 |
1 |
-64 |
64 |
64,22 |
0,0484 |
65,99 |
3,9601 |
|
3 |
0 |
77,7 |
0 |
0 |
0 |
0 |
0 |
71,8 |
34,81 |
75,34 |
5,5696 |
|
4 |
-1 |
80 |
1 |
1 |
1 |
80 |
80 |
79,38 |
0,3844 |
81,15 |
1,3225 |
|
5 |
-2 |
83,6 |
4 |
8 |
16 |
167,2 |
334,4 |
86,96 |
11,2896 |
86,96 |
11,2896 |
|
∑ |
0 |
359 |
10 |
0 |
34 |
75,8 |
693,2 |
359 |
55,176 |
368,12 |
46,9423 |
Перепишем
уравнение с учетом
 = 0 и
= 0 и = 0:
= 0:
* для линейного тренда:
 (2.17)
(2.17)
* для параболического тренда:
 (2.18)
(2.18)
Отсюда:
* для линейного тренда:
a= (2.19)
(2.19)
b=
 (2.20)
(2.20)
Получаем:
a =
 = 71.8
= 71.8
B =

* для параболического тренда:
b=
 (2.21)
(2.21)
Зная αиcнайдем, решив систему методом определителей.
Получаем: a= 75,34,c= -1,77.
Рассчитанные
значения f( )
и
)
и (
( )
при
)
при =[-2;2],
и суммы квадратов разностей теоретических
и практических значений приведены в
табл.2.2
=[-2;2],
и суммы квадратов разностей теоретических
и практических значений приведены в
табл.2.2
Для линейного тренда
δ=
Для параболического тренда
δ=
Так
как 5,25<6,85, линейный тренд является
более предпочтительной функцией, т.е.
 =f(t). В этом
случае прогноз искомого параметра
целесообразно определять по формуле
линейного тренда, т.е.
=f(t). В этом
случае прогноз искомого параметра
целесообразно определять по формуле
линейного тренда, т.е.
 =75,34+7,58*3=98,08(тыс.
т/год)
=75,34+7,58*3=98,08(тыс.
т/год)
Графики N(t) иF(t) приведены на рисунке 2.2.
Итак, планируемый размер материального потока в 2010 году, определенный методом регрессивного анализа составляет 98 080 тонн.


 )
)


 )·
)·
 )·
)·
 )
) )-N(
)-N(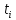 ))
))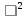
 (
( )
) (
( )-N(
)-N( ))
))