Лабы Карымов 5 семестр / методы выч 4-9

Лабороторная работа №4

по курсу «Методы вычислений»

Математический факультет, 5 семестр

Лабораторная работа	№4
Тема	Метод переменных направлений для решения краевой задачи для уравнения теплопроводности.
Ф.И.О.	Гуптор Александр Сергеевич
Группа	442(а)
Вариант	9
Дата сдачи

Рассмотрим краевую задачу для двумерного уравнения теплопроводности

U_t = U_xx + U_yy + f(x,y,t), 0<x<a, 0<y<b, 0<t<T,

U(x,y,0)=(x,y), U(0,y,t)=₁(y,t), U(a,y,t)=₂(y,t), U(x,0,t)=₃(x,t), U(x,b,t)=₄(x,t).

В области D=(0,a)x(0,b)x(0,T) построим сетку с шагами h_x=a/M₁, h_y=b/M₂, =T/N. Значение сеточной функции U(x,y,t) в узлах сетки (x_k, y_m, t_n ) будем обозначать . Наряду с основными значениями искомой сеточной функции U(x,y,t), т. е. с и , вводится промежуточное значение , которое можно формально рассматривать как значение U при t = t_n+1/2 = t_n+/2. Переход от слоя n к слою n+1 совершается в два этапа с шагами 0,5 :

(U ^n+1/2 - U ⁿ)/(0,5) = ₁U ^n+1/2 + ₂U ⁿ + f ^n+1/2, (1)

(U ⁿ⁺¹ - U ^n+1/2)/(0,5) = ₁U ^n+1/2 + ₂U ⁿ⁺¹ + f ^n+1/2 . (2)

Эти уравнения пишутся во всех внутренних узлах сетки (x,y)=(x_k ,y_m ) и для всех t_n > 0. Операторы

₁U=(U _k-1,m -2U _k,m + U_k+1,m)/h²_x , ₂U=(U _k,m-1 -2U _k,m + U_k,m+1)/h²_y ,

аппроксимируют вторые производные по х и у соответственно со вторым порядком точности.

К уравнениям (1), (2) надо добавить начальные условия

U⁰_k,m = (x _k , y_m ) , k=0,1,2,...,M₁ , m=0,1,2,...,M₂ . (3)

и разностные краевые условия в виде

Uⁿ⁺¹_k,0 = ₃(x_k , t_n+1 ) , Uⁿ⁺¹_k,M2 = ₄(x_k , t_n+1 ) ,

U^n+1/2_0,m = (₁(y_m,t_n+1) + ₁(y_m,t_n))/2 - ₂( ₁(y_m,t_n+1) - ₁(y_m,t_n ))/4 ,

U^n+1/2_M1,m = (₂(y_m,t_n+1) + ₂(y_m,t_n))/2 - ₂( ₂(y_m,t_n+1) - ₂(y_m,t_n ))/4. (4)

Схема (1) неявна по направлению х и явна по направлению у , а схема (2) неявна по направлению у и явна по направлению х. Схему (1) - (2) перепишем в виде

U^n+1/2_k-1,m-2(1+h²_x /)U^n+1/2_k,m+U^n+1/2_k+1,m= -(h²_x/h²_y)(Uⁿ_k,m-1-2(1-h²_y /)Uⁿ_k,m+Uⁿ_k,m+1)-h²_xf(x_k,y_m,t_n+1/2) (5)

Uⁿ⁺¹_k,m-1-2(1+h²_y /)Uⁿ⁺¹_k,m+Uⁿ⁺¹_k,m+1= -(h²_y/h²_x)(U^n+1/2_k-1,m-2(1-h²_x /)U^n+1/2_k,m+U^n+1/2_k+1,m)-h²_yf(x_k,y_m,t_n+1/2) (6)

Пусть задано Uⁿ_k,m . Тогда вычисляем правые части (5) , затем методом прогонки вдоль строк m=1,2,...,M₂-1 решаем задачу (5) и определяем U^n+1/2_k,m , после чего вычисляем правые части (6) и решаем задачу (6) вдоль столбцов k=1,2,...,M₁-1 , определяя Uⁿ⁺¹_k,m. При переходе от слоя n+1 к слою n+2 процедура счета повторяется, т. е. происходит все время чередование направлений.

Для выполнения работы необходимо по заданной функции U(x,y,t) найти правую часть уравнения, начальные условия и краевые условия. Найденное приближенное решение сравнить с точным при t=T

Вариант	a	b	T	U(x,y,t)
9	2	1	1	xet+y3

Текст программы:

clear;

ax=0;

bx=2;

ay=0;

by=1;

at=0;

bt=1;

x=sym('x');

y=sym('y');

t=sym('t');

u=x*exp(t)+y^3;

%--Находим функции f, fi, m1, m2, m3, m4 -- %x=sym('x');

y=sym('y');

t=sym('t');

u=x*exp(t)+y^3;

a=2;

b=1;

f=diff(u,t,1)-diff(u,x,2)-diff(u,y,2)

t=0;

fi=eval(u)

t=sym('t');

x=0;

mi1=eval(u)

x=a;

mi2=eval(u)

x=sym('x');

y=0;

mi3=eval(u)

y =b;

mi4=eval(u)

%--Строим сетку--%

M1=3;

M2=3;

N=19;

hx=(bx-ax)/M1;

hy=(by-ay)/M2;

ht=(bt-at)/N;

xk=ax:hx:bx;

ym=ay:hy:by;

tn=at:ht:bt;

%--Вычисляем граничные и краевые условия--%

%--для фи (при t=0)--%

for i=1:M1+1

for j=1:M2+1

x=xk(i);

y=ym(j);

s(i,j,1)=eval(fi);

end;

end;

%--для мю1 (при x=0)--%

for i=1:M2+1

for k=1:N+1

y=ym(i);

t=tn(k);

s(1,i,k)=eval(mi1);

end;

end;

%--для мю2 (при x=a)--%

for i=1:M2+1

for k=1:N+1

y=ym(i);

t=tn(k);

s(M1+1,i,k)=eval(mi2);

end;

end;

%--для мю3 (при y=0)--%

for i=1:M1+1

for k=1:N+1

x=xk(i);

t=tn(k);

s(i,1,k)=eval(mi3);

end;

end;

%--для мю4 (при y=b)--%

for i=1:M1+1

for k=1:N+1

x=xk(i);

t=tn(k);

s(i,M2+1,k)=eval(mi4);

end;

end;

%до сюда все хорошо!!!

%--чё то вычисляем, вроди бы, начальные значения при x=ax и x=bx и при--%

%--t=t(n)+ht/2, где n=1..N, y=y(m), где m=1..M2--%

for k=1:N

for j=2:M2

% sp(1,j,k)=exp(ym(j))-(ht-1)*(exp(ym(j+1))-2*exp(ym(j))+exp(ym(j-1)))/(hy^2);

% sp(M1+1,j,k)=(cos(2*tn(k+1))+exp(ym(j))+cos(2*tn(k))+exp(ym(j)))/2-ht*(cos(2*tn(k+1))+exp(ym(j+1))-2*(cos(2*tn(k+1))+exp(ym(j)))+cos(2*tn(k+1))+exp(ym(j-1)))/(hy^2)+(cos(2*tn(k))+exp(ym(j+1))-2*(cos(2*tn(k))+exp(ym(j)))+cos(2*tn(k))+exp(ym(j-1)))/(hy^2);

sp(1,j,k)=exp(ym(j));

sp(M1+1,j,k)=(cos(2*tn(k+1))+exp(ym(j))+cos(2*tn(k))+exp(ym(j)))/2-(ht/((hy^2)))*((cos(2*tn(k+1))+exp(ym(j+1))-2*(cos(2*tn(k+1))+exp(ym(j)))+cos(2*tn(k+1))+exp(ym(j-1)))-(cos(2*tn(k))+exp(ym(j+1))-2*((cos(2*tn(k))+exp(ym(j))))+cos(2*tn(k))+exp(ym(j-1))));

end;

end;

disp('asd');

sp(1,:,N)

sp(M1+1,:,N)

%--вычислим функцию fp--%

for k=1:N+1

for j=1:M2+1

for i=1:M1+1

x=xk(i);

y=ym(j);

t=tn(k)+ht/2;

fp(i,j,k)=eval(f);

% fp(i,j,k)=-(2*x^3)*sin(2*t)-6*x*cos(2*t)-exp(y);

end;

end;

end;

%--сама разностная схема--%

a1=1;

b1=2*(1+((hx^2)/ht));

c1=1;

a2=1;

b2=2*(1+((hy^2)/ht));

c2=1;

tol=0;

k=1;

for k=1:N

%--вычисляем функцию в узлах F(i,j,k)--%

for i=2:M1

for j=2:M2

F(i,j,k)=-((hx^2)/(hy^2))*(s(i,j-1,k)-2*(1-(hx^2)/ht)*s(i,j,k)+s(i,j+1,k))-(hx^2)*fp(i,j,k);

end;

end;

%--решаем уравнение a1*sp(i-1,j,k)+b1*sp(i,j,k)+c1*sp(i+1,j,k)=F(i,j,k)--%

for i=2:M1

alphap(1)=0;

betap(1)=sp(1,j,k);

for i=2:M1+1

alphap(i)=c1/(b1-a1*alphap(i-1));

betap(i)=(a1*betap(i-1)-F(i-1,j,k))/(b1-a1*alphap(i-1));

end;

for i=M1:-1:1

sp(i,j,k)=alphap(i+1)*sp(i+1,j,k)+betap(i+1);

end;

end;

%--вычисляем функцию в узлах Fp(i,j,k)--%

for i=2:M1

for j=2:M2

Fp(i,j,k)=-(((hy^2)/(hx^2))*(sp(i-1,j,k)-2*((1-((hy^2)/ht))*sp(i,j,k))+sp(i+1,j,k)))-(hy^2)*fp(i,j,k);

end;

end;

%--решаем уравнение a2*s(i-1,j,k+1)+b2*s(i,j,k+1)+c2*s(i+1,j,k+1)=Fp(i,j,k)--%

for i=2:M1

alpha(1)=0;

beta(1)=s(i,1,k+1);

for j=2:M2+1

alpha(j)=c2/(b2-a2*alpha(j-1));

beta(j)=(a2*beta(j-1)-Fp(i,j-1,k))/(b2-a2*alpha(j-1));

end;

for j=M2:-1:2

s(i,j,k+1)=alpha(j+1)*s(i,j+1,k+1)+beta(j+1);

end;

end;

end;

be=N+1;

t=tn(be);

for i=1:M1+1

for j=1:M2+1

uuu(i,j)=s(i,j,be);

x=xk(i);

y=ym(j);

uu(i,j)=eval(u);

end;

end;

%for i=2:M1

% for j=2:M2

% uuu(i,j)=uu(i,j)+0.1;

% end;

%end;

uuu(2,2)=uuu(2,2)+0.65;

uuu(2,3)=uuu(2,3)+0.65;

uuu(3,2)=uuu(3,2)+0.55;

uuu(3,3)=uuu(3,3)+0.3;

tol=max(max(abs(uu-uuu)))

%surfc(xk,ym,s(:,:,N+1))

surfc(xk,ym,uu);

hold on;

surfc(xk,ym,uuu);

hold off;

%surfc(xk,ym,uu);

uuu(2,2)=uuu(2,2)+0.65;

uuu(2,3)=uuu(2,3)+0.65;

uuu(3,2)=uuu(3,2)+0.55;

uuu(3,3)=uuu(3,3)+0.3;

uuu

uu;

График:

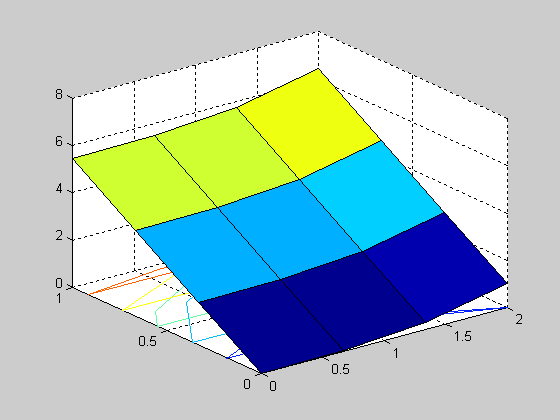
Точное решение

-1.0000 -0.5000 0 0.5000

-0.5348 1.7224 1.8588 0.9652

0.2985 1.2822 1.8716 1.7985

1.7183 2.2183 2.7183 3.2183

Найденное решение

-1.0000 -0.5000 0 0.5000

-0.5348 1.7224 1.8588 0.9652

0.2985 1.2822 1.8716 1.7985

1.7183 2.2183 2.7183 3.2183

Погрешность

0.9015