Министерство образования и науки РФ

Государственное образовательное учреждение

Высшего профессионального образования

«Ижевский Государственный Технический Университет им. М.Т.Калашникова»

Кафедра «Вычислительная Техника»

Отчёт по курсовой работе

по дисциплине:

«Основы теории управления»

(вариант 2ВКГ)

Выполнил: студент гр. 5-78-1,

Принял: Афанасьев В.А.

Ижевск, 2012

Исходные данные

Задание 2

Первая схема В

Корни уравнения К

p₁ = -10

p₂ = -5+4j

p₃ = -5-4j

Вторая схема Г

k₁ = 10

k₂ = 100

T₁ = 0.1c

1. Для схемы В написать передаточные функции по команде и помехам. На основании принципа суперпозиции написать выражение для реакции системы на команду и помеху.

Дополнительно отметим на первой схеме сигналы z,x,x₁,y₁

Пусть W₂’(p) = W₂(p) – 1.

Из выражения передаточной функции получаем:

Y(p)=Y₁(p)+F₂(p)

Y₁(p) = X₁(p)*W₁(p)

X₁(p) = X(p)+F₁(p)

X(p) = G(p) +Z(p)

Z(p) = Y₁(p)*(-W₂’(p))

Отсюда выражаем Y₁(p):

Y₁(p) = W₁(p)*( Y₁(p)*(-W₂’(p))+ G(p)+ F₁(p))

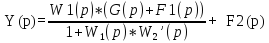
или

Т.е.

- передаточная функция по команде g(p).

- передаточная функция по помехе f₁(p).

2. По заданным корням характеристического уравнения записать общее решение однородного дифференциального уравнения, определить 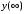, указать расположение корней на плоскости и по их расположению отметить характер переходного процесса (монотонный, немонотонный). Определить устойчивость системы.

Общее решение дфференциального уравнения определяется по формуле:

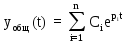
Т.к. имеются пары чисто мнимых корней, то уравнение будет иметь вид:

y_общ(t) = С₁e^-10t + C₂e^(-5+4j)t + C₃e^(-5-4j)t = С₁e^-10t + Ae^-5tsin(4t+ψ)

Поэтому

Характер переходного процесса немонотонный. Корни характеристического уравнения находятся в левой полуплоскости. Система устойчива.

3. Для схемы по варианту задания составить передаточную функцию системы, разомкнутой по цепи единичной отрицательной обратной связи, передаточную функцию замкнутой системы, характеристические уравнения разомкнутой и замкнутой систем.

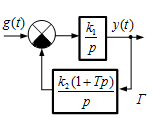
а). Передаточная функция для разомкнутой системы:

Характеристическое уравнение разомкнутой системы:

A(p) = p²=0.

б). Передаточная функция замкнутой системы:

Характеристическое уравнение замкнутой системы:

.

4. Определить величину ошибки установившегося режима с помощью коэффициентов ошибок

Передаточная функция ошибки от команды g(t):

Разделим числитель на знаменатель:

Получаем коэффициенты:

с₀ = 0

с₁ = 0

с₂ =

с₃ =

и т.д.

Пусть g(t) = g₀ = const, тогда 0

Пусть g(t) = at, где a = const, тогда 0

Пусть g(t) = a²t, тогда

Пусть g(t) = a³t, тогда

5. Исследовать устойчивость разомкнутой и замкнутой системы по Стодоле.

а). Для разомкнутой системы:

A(p) = p² = 0

Т.к. имеется p, то система нейтрально устойчива.

б). Для замкнутой системы:

D(p) = = 0

Т.к. все коэффициенты больше 0, то система устойчива.

6. Исследовать устойчивость разомкнутой и замкнутой системы по Гурвицу.

а). Для разомкнутой системы:

A(p) = p²=0

Система с передаточной функцией A(p) нейтрально устойчива.

б). Для замкнутой системы:

D(p) =

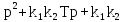
a₀ = k₁k₂=1000>0

₁ = a₁ = 100>0

Система устойчива, так как все определители больше 0.

7. Исследовать устойчивость разомкнутой и замкнутой системы по Михайлову

а). Для разомкнутой системы:

A(p) = p²

А(jw) = -w²

График АПХ имеет вид:

Условие Михайлова:

В данном случае n=2 и график АПХ проходит через одну четверть, поэтому система с характеристическим уравнением A(p) неустойчива.

б). Для замкнутой системы:

D(p) =

D(jw) = -w²+k₁k₂+jw=X(w)+jY(w)

График АПХ имеет вид:

Как видно при увеличении частоты w график АПХ движется против часовой стрелки и проходит последовательно через две четверти. Следовательно, система устойчива.

8. Исследовать устойчивость замкнутой системы по Найквисту (по логарифмическим характеристикам разомкнутой системы).

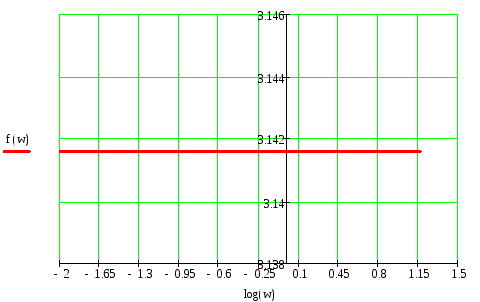
Система устойчива, т.к. график ЛФХ лежит выше и не пересекает -.

9. Исследовать устойчивость замкнутой системы по Найквисту (по АФХ разомкнутой системы).

АФХ имеет вид:

Как видно, система устойчива, так как кривая АФХ не охватывает критическую точку(-1;0).