-
Расчетная часть
Задание 1
По результатам обследования бюджетов домохозяйств региона имеются данные о денежных доходах и потреблении: Таблица 1. Данные обследования бюджетов домохозяйств региона
|
№ семьи п/п |
Среднемесячный доход на члена семьи, тыс. руб. |
Потребление рыбы и рыбопродуктов в расчете на одну потребительскую единицу в месяц, кг |
|
1 |
0,4 |
0,2 |
|
2 |
0,5 |
0,3 |
|
3 |
0,9 |
1,0 |
|
4 |
1,0 |
1,5 |
|
5 |
1,2 |
1,7 |
|
6 |
1,6 |
3,0 |
|
7 |
2,3 |
3,2 |
|
8 |
2,6 |
3,5 |
|
9 |
3,0 |
3,6 |
|
10 |
3,5 |
4 |
Для анализа взаимосвязи между среднедушевым доходом семьи и потреблением рыбопродуктов определите: 1. Коэффициент тесноты связи. 2. Уравнение связи (регрессионную модель) и поясните значение его параметров. 3. Коэффициенты эластичности потребления от дохода: а) частные – для каждой семьи; б) средний – для данной совокупности семей. Сделайте выводы.
Решение: 1) Факторным признаком является – среднемесячный доход на члена семьи (X), а результативным – потребление рыбопродуктов (Y). Вычислим коэффициент тесноты связи между двумя указанными факторами по формуле:
Для нахождения соответствующих сумм составим расчетную таблицу: Таблица 2. Расчетные данные
|
|
X |
Y |
X2 |
Y2 |
XY |
|
|
0,4 |
0,2 |
0,16 |
0,04 |
0,08 |
|
|
0,5 |
0,3 |
0,25 |
0,09 |
0,15 |
|
|
0,9 |
1 |
0,81 |
1 |
0,9 |
|
|
1 |
1,5 |
1 |
2,25 |
1,5 |
|
|
1,2 |
1,7 |
1,44 |
2,89 |
2,04 |
|
|
1,6 |
3 |
2,56 |
9 |
4,8 |
|
|
2,3 |
3,2 |
5,29 |
10,24 |
7,36 |
|
|
2,6 |
3,5 |
6,76 |
12,25 |
9,1 |
|
|
3 |
3,6 |
9 |
12,96 |
10,8 |
|
|
3,5 |
4 |
12,25 |
16 |
14 |
|
∑ |
17 |
22 |
39,52 |
66,72 |
50,73 |
Подставив в формулу соответствующие суммы, получим:
Вывод.
Поскольку значение коэффициента
корреляции близко к 1, то то согласно
таблице Чэддока, между среднемесячным
доходом и потреблением рыбопродуктов
имеет место тесная корреляционная
связь, близкая к прямолинейной, причем
– связь прямая, т.е. при увеличении
среднедушевого дохода на члена семьи
увеличивается потребление рыбопродуктов.
2) Вычислим линейное
уравнение связи между среднедушевым
доходом семьи и потреблением рыбопродуктов.
В качестве уравнения, выражающего
зависимость между указанными факторами,
возьмем линейное уравнение:
.
Определим
параметры 
и 
по
формулам:
и
Подставив в данные формулы значения для сумм, получим:
Таким
образом, полученная регрессионная
модель имеет вид:
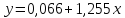Вывод.
Параметр 
показывает
начальный уровень потребления
рыбопродуктов, а 
показывает,
что с увеличение среднедушевого дохода
на 1 тыс.руб. потребление рыбопродуктов
увеличивается в среднем на 1,255 кг.
Рис.
1 Фактические данные и регрессионная
модель.